2022. 11. 3. 11:04ㆍView Synthesis
Mip-NeRF 360: Unbounded Anti-Aliased Neural Radiance Fields
Jonathan T. Barron, Ben Mildenhall, Dor Verbin, Pratul P. Srinivasan, Peter Hedman
Abstract
Neural Radiance Fields (NeRF)은 물체와 공간의 작은 경계 영역에서 인상적인 뷰 합성 결과를 보여주었지만, 카메라가 임의의 방향을 가리키고 콘텐츠가 임의의 거리에 존재할 수 있는 "unbounded" 장면에서 어려움을 겪는다.
이 설정에서 기존 NeRF-like 모델은 종종 블러하거나 저해상도 렌더링을 생성하며(근처와 먼 물체의 불균형 세부 사항과 규모로 인해) 학습 속도가 느리고 작은 이미지 세트에서 큰 장면을 재구성하는 작업의 고유한 모호성으로 인해 아티팩트를 나타낼 수 있다.
우리는 비선형 장면 매개 변수화, 온라인 distillation 및 새로운 왜곡 기반 정규화기를 사용하여 무한 장면이 제시하는 과제를 극복하는 mip-NeRF(샘플링 및 앨리어싱을 다루는 NeRF 변형)의 확장을 제시한다.
카메라가 점을 중심으로 360도 회전하는 장면을 목표로 하기 때문에 "mip-NeRF 360"이라고 부르는 우리 모델은 mip-NeRF에 비해 평균 제곱 오차를 57% 줄이고, 매우 복잡하고 제한되지 않은 실제 장면을 위한 현실적인 합성 뷰와 상세한 depth 맵을 생성할 수 있다.
Neural Radiance Fields (NeRF)은 좌표 기반 다층 퍼셉트론(MLP)의 가중치 내에서 장면의 부피 밀도 및 색상을 인코딩하여 매우 사실적인 장면 렌더링을 합성한다.
이 접근 방식은 사진 사실적 시각 합성을 향한 상당한 진전을 가능하게 했다[33].
그러나 NeRF는 ray를 따라 무한히 작은 3D 포인트를 사용하여 MLP에 대한 입력을 모델링하며, 이는 다양한 해상도의 뷰를 렌더링할 때 앨리어싱을 발생시킨다.
Mip-NeRF는 대신 원뿔을 따라 부피 frustum에 대해 추론하도록 NeRF를 확장함으로써 이 문제를 해결했다[3].
이것은 품질을 향상시키지만, NeRF와 mip-NeRF 모두 카메라가 어떤 방향을 향할 수 있고 장면 콘텐츠가 어느 거리에나 존재할 수 있는 무한 장면을 처리할 때 어려움을 겪는다.
본 연구에서는 그림 1과 같이 이러한 무한 장면의 현실적인 렌더링을 생성할 수 있는 "mip-NeRF 360"이라고 하는 mip-NeRF의 확장을 제시한다.

NeRF-like 모델을 대규모 무한 장면에 적용하는 것은 세 가지 중요한 문제를 제기한다:
1. Parameterization. 무한 360도 장면은 유클리드 공간의 임의로 큰 영역을 차지할 수 있지만, mip-NeRF는 3D 장면 좌표가 유계 영역에 있어야 한다.
2. Efficiency. 크고 상세한 장면은 더 많은 네트워크 용량이 필요하지만, 학습 중에 각 ray를 따라 큰 MLP를 조밀하게 쿼리하는 것은 비용이 많이 든다.
3. Ambiguity. 무한 장면의 내용은 임의의 거리에 있을 수 있으며 적은 수의 ray로만 관찰되어 2D 이미지에서 3D 콘텐츠를 재구성하는 본질적인 모호성을 악화시킨다.
Parameterization.
투시 투영으로 인해 카메라에서 멀리 떨어진 물체는 이미지 평면의 작은 부분을 차지하지만, 근처에 배치되면 이미지의 더 많은 부분을 차지하고 자세히 볼 수 있습니다.
따라서 3D 장면의 이상적인 매개 변수화는 가까운 콘텐츠에 더 많은 용량을 할당하고 먼 콘텐츠에 더 적은 용량을 할당해야 한다.
NeRF 외부에서, 기존의 뷰 합성 방법은 투영 파노라마 공간[2, 4, 9, 16, 23, 27, 36, 46, 54]에서 장면을 매개 변수화하거나 다중 뷰 스테레오를 사용하여 복구된 일부 프록시 지오메트리[17, 26, 41] 내에 장면 콘텐츠를 내장하여 이를 해결한다.
NeRF의 성공의 한 측면은 특정 장면 유형을 적절한 3D 매개 변수화와 결합하는 것이다.
원래의 NeRF 논문[33]은 마스크된 배경을 가진 물체의 360도 캡처와 모든 이미지가 거의 동일한 방향을 향하는 정면 장면에 초점을 맞췄다.
마스크된 객체의 경우 NeRF는 3D 유클리드 공간에서 장면을 직접 매개 변수화했지만, 전면 장면의 경우 NeRF는 투영 공간에서 정의된 좌표(정규화된 장치 좌표 또는 "NDC" [5])를 사용했다.
Z축을 따른 거리가 차이(역거리)에 해당하는 경계 큐브로 무한히 깊은 카메라 frustum을 비틀어 줌으로써, NDC는 투시 투영 기하학과 일치하는 방식으로 NeRF MLP의 용량을 효과적으로 재할당한다.
그러나 단일 방향이 아닌 모든 방향으로 제한되지 않는 장면에는 다른 매개 변수화가 필요합니다.
이 아이디어는 원격 물체를 모델링하기 위해 추가 네트워크를 사용한 NeRF++ [51]와 원점을 향해 먼 점을 축소하는 공간 워핑 절차를 제안한 DONeRF [34]에 의해 탐구되었다.
이 두 가지 접근 방식은 모두 Z축을 따라서가 아니라 모든 방향에서 NDC와 다소 유사하게 동작한다.
이 작업에서 우리는 이 아이디어를 mip-NeRF로 확장하고 볼륨(점이 아닌)에 부드러운 매개 변수화를 적용하는 방법을 제시하고, 무한 장면에 대한 자체 매개 변수화를 제시한다.
Efficiency.
무한 장면을 다루는 데 있어 한 가지 근본적인 도전은 그러한 장면이 종종 크고 상세하다는 것이다.
NeRF-like 모델은 놀랄 만큼 적은 수의 가중치를 사용하여 장면의 물체 또는 영역을 정확하게 재현할 수 있지만, NeRF MLP의 용량은 점점 더 복잡한 장면 콘텐츠에 직면할 때 포화된다.
또한 큰 장면은 표면을 정확하게 위치시키기 위해 각 ray를 따라 훨씬 더 많은 샘플이 필요하다.
예를 들어, 객체에서 건물까지 NeRF를 확장할 때, Martin-Brualla et al.[30]은 MLP 숨겨진 유닛의 수를 두 배로 늘리고 MLP 평가의 수를 8배 증가시켰다.
이러한 모델 용량의 증가는 비용이 많이 듭니다.
NeRF는 이미 학습하는 데 여러 시간이 걸리며, 이 시간에 ~40배를 추가로 곱하는 것은 대부분의 사용에서 엄청나게 느립니다.
이러한 학습 비용은 NeRF 및 mip-NeRF에서 사용하는 coarse-to-fine 리샘플링 전략으로 인해 악화됩니다: MLP는 "coarse" 및 "fine" ray 간격을 사용하여 여러 번 평가되며, 두 경로에서 이미지 재구성 loss를 사용하여 supervise됩니다.
장면의 "coarse" 렌더링이 최종 이미지에 기여하지 않기 때문에 이 접근법은 낭비적이다.
여러 척도로 supervise되는 단일 NeRF MLP를 학습하는 대신, 우리는 두 개의 MLP를 학습할 것이다: "proposal MLP" 및 "NeRF MLP".
proposal MLP는 체적 밀도(색상은 아님)를 예측하고 이러한 밀도는 NeRF MLP에 제공된 새로운 간격을 재샘플링하는 데 사용되어 이미지를 렌더링한다.
결정적으로, proposal MLP에 의해 생성된 가중치는 입력 이미지를 사용하여 supervise되지 않고, 대신 NeRF MLP에 의해 생성된 히스토그램 가중치로 supervise된다.
이를 통해 우리는 비교적 몇 번 평가되는 큰 NeRF MLP를 몇 번 더 평가하는 작은 proposal MLP와 함께 사용할 수 있다.
결과적으로, 우리 전체 모델의 총 용량은 mip-NeRF(~15배)보다 훨씬 커서 렌더링 품질이 크게 향상되지만, 우리의 학습 시간은 약간만 증가한다(~2배).
우리는 이 접근 방식을 일종의 "online distillation"라고 생각할 수 있다: "distillation"은 일반적으로 이미 학습된 대형 네트워크의 출력에 일치하도록 소규모 네트워크를 학습시키는 것을 의미하지만 [19] 여기서는 두 네트워크를 동시에 학습시켜 NeRF MLP가 예측한 출력의 구조를 proposal MLP "online"으로 distill한다.
NeRV [47]는 가시성과 간접 조도를 모델링하기 위해 MLP를 대략적인 렌더링 적분으로 학습하는 완전히 다른 작업에 대해 유사한 종류의 online distillation을 수행한다.
우리의 online distillation 접근법은 supervision을 위해 ground-truth depth를 사용하지만, DONeRF에 사용되는 "샘플링 오라클 네트워크"와 정신적으로 유사하다[34].
TermiNeRF [39]에서 관련 아이디어가 사용되었지만, 그러한 접근 방식은 추론을 가속화하고 실제로 학습을 느리게 한다(NeRF는 수렴하도록 학습되고 이후 추가 모델은 학습된다).
학습된 "proposer" 네트워크는 NeRF의 세부 정보 [1]에서 조사되었지만 25%의 속도 향상을 달성하는 데 그치는 반면, 우리의 접근 방식은 학습을 300% 가속화한다.
여러 연구에서 학습된 NeRF를 신속하게 렌더링할 수 있는 형식으로 distill하거나 "bake"하려고 시도했지만 [18, 40, 50] 이러한 기술은 학습을 가속화하지 않는다.
octrees [43] 또는 경계 볼륨 계층[42]과 같은 계층적 데이터 구조를 통해 ray 추적을 가속화하는 아이디어는 렌더링 문헌에서 잘 탐구되어 있지만, 이러한 접근 방식은 장면의 기하학에 대한 a-priori 지식을 가정하고 따라서 자연스럽게 역 렌더링 컨텍스트로 일반화하지 않는다, 장면의 지오메트리를 알 수 없으므로 복구해야 합니다.
실제로, NeRF-like 모델을 최적화하면서 octree 가속 구조를 구축했음에도 불구하고, Neural Sparse Voxel Fields 접근 방식은 학습 시간을 크게 줄이지 않는다[28].
Ambiguity.
NeRF는 전통적으로 장면의 많은 입력 이미지를 사용하여 최적화되지만, 새로운 카메라 각도에서 사실적인 합성 뷰를 생성하는 NeRF를 복구하는 문제는 여전히 근본적으로 제약이 부족합니다 — NeRF의 무한한 제품군은 입력 이미지를 설명할 수 있지만, 작은 부분 집합만이 새로운 뷰에 대해 허용 가능한 결과를 생성합니다.
예를 들어, NeRF는 각 이미지를 해당 카메라 바로 앞에 텍스처 평면으로 재구성하여 모든 입력 이미지를 재생성할 수 있습니다.
원래의 NeRF 논문은 rectifier [33] 전에 NeRF MLP의 밀도 헤드에 가우시안 노이즈를 주입하여 모호한 장면을 정규화했으며, 이는 밀도가 0 또는 무한대로 중력화하도록 장려한다.
비록 이것이 반투명 밀도를 떨어뜨림으로써 일부 "floaters"를 감소시키지만, 우리는 그것이 우리의 더 어려운 작업에 불충분하다는 것을 보여줄 것이다.
밀도[18]에 대한 강력한 loss 또는 표면 [35, 53]에 대한 평활도 패널티와 같은 NeRF를 위한 다른 정규화기가 제안되었지만, 이러한 솔루션은 우리와 다른 문제(각각 느린 렌더링 및 평활하지 않은 표면)를 해결한다.
또한, 이러한 정규화기는 NeRF에서 사용하는 포인트 샘플을 위해 설계된 반면, 우리의 접근 방식은 각 mip-NeRF ray를 따라 정의된 연속 가중치로 작동하도록 설계되었다.
이 세 가지 문제는 mip-NeRF의 검토 후 섹션 2, 3 및 4에서 각각 다루어질 것이다.
우리는 도전적인 실내 및 실외 장면으로 구성된 새로운 데이터 세트를 사용하여 이전 작업에 대한 우리의 개선을 보여줄 것이다.
우리의 결과는 애니메이션화되었을 때 가장 잘 평가되기 때문에, 우리는 독자들에게 우리의 보충 비디오를 볼 것을 촉구한다.
1. Preliminaries: mip-NeRF
먼저 완전히 학습된 mip-NeRF [3]가 장면 r(t) = o+td로 주조된 단일 ray의 색상을 렌더링하는 방법을 설명하겠습니다, 여기서 o와 d는 각각 ray의 원점과 방향이고 t는 ray를 따라 거리를 나타냅니다.
mip-NeRF에서 거리 t의 정렬된 벡터가 정의되고 ray는 간격 T_i = [t_i, t_(i+1))의 집합으로 분할됩니다.
각 간격에 대해 우리는 간격(이미지 평면의 ray의 초점 거리와 픽셀 크기에 의해 결정되는 반지름)에 해당하는 conical frustum의 평균과 공분산 (μ, Σ) = r(T_i)을 계산하고 통합 위치 인코딩을 사용하여 이러한 값을 특징짓는다:

이것은 conical frustum에 가까운 가우시안과 관련하여 NeRF가 사용하는 인코딩의 기대치이다.
이러한 피쳐는 밀도 τ와 색상 c를 출력하는 가중치 Θ_NeRF에 의해 매개 변수화된 MLP에 대한 입력으로 사용된다:

뷰 방향 d도 MLP에 대한 입력으로 제공되지만 단순성을 위해 이를 생략한다.
이러한 밀도와 색상으로 수치 직교 [31]를 사용하여 볼륨 렌더링 적분을 근사한다:

, 여기서 C(r, t)는 최종 렌더링 픽셀 색상이다.
구성에 의해, 알파 합성 가중치 w는 1보다 작거나 같도록 보장된다.
ray는 먼저 카메라의 가까운 면과 먼 면의 [t_n, t_f]에 걸친 균일한 분포로부터 정렬된 샘플인 균일한 간격의 "coarse" 거리 t^c를 사용하여 렌더링된다:
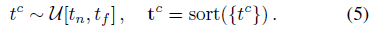
학습 중에 이 샘플링은 확률적이지만, 평가 중에 샘플은 t_n에서 t_f까지 균일하게 떨어져 있다.
MLP가 "coarse" 가중치 w^c의 벡터를 생성한 후, 역변환 샘플링을 사용하여 t^c와 w^c에 의해 정의된 히스토그램에서 "fine" 거리 t^f를 샘플링한다:
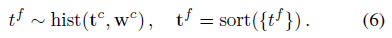
coarse 가중치 w^c는 장면 내용에 집중되는 경향이 있기 때문에, 이 전략은 샘플링 효율성을 향상시킨다.
Mip-NeRF는 coarse 및 fine 재구성 loss의 가중 조합을 최소화하기 위해 그래디언트 강하를 통해 MLP 매개 변수 Θ_NeRF를 최적화하여 복구된다:
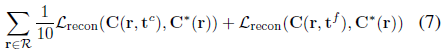
, 여기서 R은 우리의 학습 데이터에서 ray 세트이고 C*(r)는 입력 이미지에서 얻은 ray r에 해당하는 ground truth 색상이고 L_recon은 평균 제곱 오차이다.
2. Scene and Ray Parameterization
무한 장면의 점의 매개 변수화에 대한 이전 연구가 있지만, 이것은 가우시안을 매개 변수화해야 하는 mip-NeRF 컨텍스트에 대한 솔루션을 제공하지 않는다.
이를 위해 먼저 f(x)를 R^n → R^n(우리의 경우, n = 3)에서 매핑되는 부드러운 좌표 변환으로 정의하자.
우리는 이 함수의 선형 근사를 계산할 수 있다:
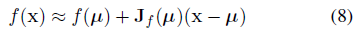
여기서 J_f(μ)는 μ에서 f의 야코비안이다
이를 통해 다음과 같이 (μ, Σ)에 f를 적용할 수 있다:
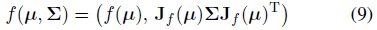
이것은 기능적으로 고전적인 확장 Kalman filter [21]와 동등하며, 여기서 f는 상태 전이 모델이다.
f에 대한 우리의 선택은 다음과 같은 수축이다:
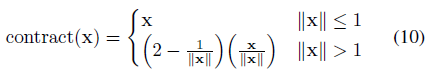
이 설계는 NDC와 동일한 동기를 공유한다: 거리 지점은 거리가 아닌 불균형(비교 거리)에 비례하여 분포되어야 한다.
우리 모델에서, 식 1에 따라 유클리드 공간에서 mip-NeRF의 IPE 기능을 사용하는 대신, 우리는 이 수축된 공간에서 유사한 기능(부록 참조)을 사용한다: γ(contract(μ, Σ))
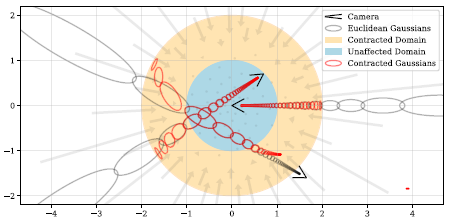
이 매개 변수화의 시각화는 그림 2를 참조하십시오.
3D 좌표를 매개 변수화하는 방법 외에도 ray 거리 t를 어떻게 선택해야 하는지에 대한 문제가 있다.
NeRF에서 이것은 보통 식 5에 따라 가까운 면과 먼 면으로부터 균일하게 샘플링함으로써 수행된다.
그러나 NDC 매개 변수화가 사용되는 경우, 이 균일한 간격의 일련의 샘플은 실제로 역 depth(불일치)로 균일하게 이격된다.
이 설계 결정은 카메라가 한 방향으로만 향할 때 제한되지 않는 장면에는 적합하지만 모든 방향으로 제한되지 않는 장면에는 적용되지 않는다.
따라서 우리는 disparity의 거리 t를 명시적으로 샘플링할 것이다(이 간격의 자세한 동기는 [32] 참조).
disparity 측면에서 ray를 매개 변수화하기 위해 우리는 유클리드 ray 거리 t와 "normalized" ray 거리 s 사이의 가역 매핑을 정의한다:
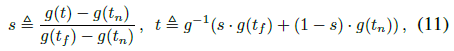
, 여기서 g(·)는 어떤 가역 스칼라 함수이다.
이것은 [t_n, t_f]에 매핑되는 "normalized" ray 거리 s ∈ [0, 1]을 제공한다.
이 논문에서 우리는 어떤 것이 더 편리하고 직관적이냐에 따라 t-space 또는 s-space에서 ray를 따른 거리를 언급할 것이다.
g(x) = 1/x로 설정하고 s-space에 균일하게 분포된 ray 샘플을 구성함으로써, 우리는 t-distance가 disparity에서 선형적으로 분포된 ray 샘플을 생산한다. (일반적으로, g(x) = log(x)를 설정하면 DONeRF의 로그 간격[34]이 산출됩니다.)
우리 모델에서는 t 거리를 사용하여 식 5와 6의 샘플링을 수행하는 대신 s 거리를 사용합니다.
이는 초기 샘플이 선형적으로 disparity가 있을 뿐만 아니라 가중치 w의 개별 간격에서 후속 리샘플링도 유사하게 분포된다는 것을 의미합니다.
그림 2의 중앙에 있는 카메라에서 볼 수 있듯이, ray 샘플의 선형 불일치 간격은 contract(·)을 상쇄합니다.
효과적으로, 우리는 우리의 장면 좌표 공간을 우리의 역 depth 간격과 공동 설계했고, 이는 원본 NeRF 논문의 매우 효과적인 설정과 매우 유사한 무한 장면의 매개 변수화를 제공한다: 경계 공간 내에서 균등하게 배열된 ray 간격.
3. Coarse-to-Fine Online Distillation
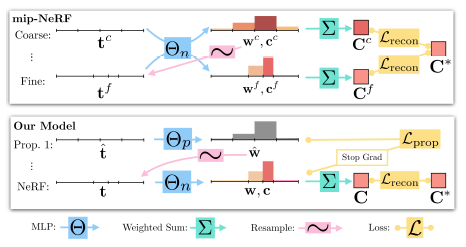
논의된 바와 같이, mip-NeRF는 "coarse" ray 간격을 사용하여 MLP를 한 번 평가하고 다시 "fine" ray 간격을 사용하여 평가하고, 두 수준에서 이미지 재구성 loss를 사용하여 supervise하는 coarse-to-fine 재샘플링 전략(그림 3)을 사용한다.
대신 "NeRF MLP" Θ_NeRF (NeRF 및 mip-NeRF에서 사용하는 MLP와 유사하게 동작)와 "proposal MLP" Θ_prop의 두 가지 MLP를 학습한다.
proposal MLP는 식 4에 따라 proposal 가중치 벡터 ^w로 변환되는 체적 밀도를 예측하지만, 색상은 예측하지 않는다.
이러한 proposal 가중치 ^w는 자체 가중치 벡터 w(및 이미지 렌더링에 사용하기 위한 색상 추정치)를 예측하는 NeRF MLP에 제공된 s-intervals을 샘플링하는 데 사용된다.
결정적으로, proposal MLP는 입력 이미지를 재현하도록 학습되지 않고 대신 NeRF MLP에 의해 생성된 가중치 w를 제한하도록 학습된다.
두 MLP는 랜덤으로 초기화되고 공동으로 학습되므로, 이 supervision은 proposal MLP에 대한 NeRF MLP의 지식을 일종의 "online distillation"으로 생각할 수 있다.
우리는 큰 NeRF MLP와 작은 proposal MLP를 사용하고, 많은 샘플로 proposal MLP를 반복적으로 평가하고 재샘플링하지만 (일부 수치와 토론은 명확성을 위해 단일 재샘플만 보여준다) 더 작은 샘플 세트로 NeRF MLP를 한 번만 평가한다.
이것은 mip-NeRF보다 훨씬 더 높은 용량을 가지고 있지만 학습 비용이 적당히 더 많이 드는 것처럼 행동하는 모델을 제공한다.
우리가 보여줄 것처럼, 제안 분포를 모델링하기 위해 작은 MLP를 사용하는 것은 정확도를 감소시키지 않으며, 이는 NeRF MLP를 distilling하는 것이 뷰 합성보다 쉬운 작업임을 시사한다.
이러한 온라인 distillation에는 proposal MLP(^t, ^w)와 NeRF MLP(t, w)에 의해 방출되는 히스토그램이 일관되도록 장려하는 loss 함수가 필요하다.
처음에 이 문제는 두 히스토그램 사이의 차이를 최소화하는 것이 잘 확립된 작업이기 때문에 사소한 것처럼 보일 수 있지만, 이러한 히스토그램 t와 ^t의 "bins"이 유사할 필요는 없다는 것을 기억하십시오 — 실제로 proposal MLP가 장면 콘텐츠가 존재하는 거리 집합을 성공적으로 도태하는 경우 ^t와 t는 매우 상이할 것입니다.
문헌에는 동일한 bins를 가진 두 히스토그램 간의 차이를 측정하기 위한 수많은 접근법이 포함되어 있지만 [12, 29, 38], 우리의 사례는 상대적으로 충분히 조사되지 않았다.
이 문제는 하나의 히스토그램 bins 내의 내용 분포에 대해 아무것도 가정할 수 없기 때문에 어렵다.
가중치가 0이 아닌 구간은 전체 구간에 걸쳐 가중치의 균일한 분포를 나타낼 수 있고, 해당 구간의 어느 곳에 위치한 델타 함수 또는 무수한 다른 분포를 나타낼 수 있다.
따라서 우리는 다음과 같은 가정 하에 loss를 구성한다.
어떤 식으로든 질량의 단일 분포를 사용하여 두 히스토그램을 모두 설명할 수 있다면 loss는 0이어야 합니다.
0이 아닌 loss는 두 히스토그램이 동일한 "true" 연속적인 질량 분포의 반사일 수 없는 경우에만 발생할 수 있다.
이 개념의 시각화는 부록을 참조하십시오.
이를 위해 먼저 구간 T와 겹치는 모든 proposal 가중치의 합을 계산하는 함수를 정의한다.
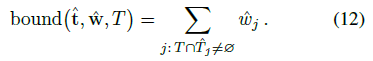
두 히스토그램이 서로 일치하면 (t, w)의 모든 구간(T_i, w_i)에 대해 w_i ≤ bound(^t, ^w, T_i)를 유지해야 합니다.
이 특성은 측정 이론에서 외부 측정의 부가성 특성과 유사합니다 [14].
loss는 이 불평등을 위반하고 이 한계를 초과하는 모든 잉여 히스토그램 질량에 불이익을 줍니다.
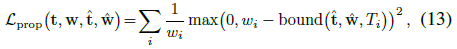
이 loss는 통계와 컴퓨터 비전에서 자주 사용되는 치 제곱 히스토그램 거리의 반사분위수 버전과 유사하다[38].
이러한 loss는 NeRF MLP에 의해 내포된 분포를 과소평가하는 proposal 가중치에 대해 불이익을 주기를 원하기 때문에 비대칭적입니다 — proposal 가중치가 NeRF 가중치보다 더 coarse할 가능성이 있기 때문에 과대 추정치가 예상됩니다, 따라서 그 위에 상부 포락선을 형성할 것입니다.
w_i에 의한 나눗셈은 경계에 대한 이 loss의 그래디언트가 경계가 0일 때 일정한 값임을 보장하며, 이는 잘 동작하는 최적화로 이어진다.
t와 ^t가 정렬되어 있기 때문에, 식 13은 합계 면적 표를 사용하여 효율적으로 계산할 수 있습니다 [11].
이 loss는 거리 t의 단조로운 변환에 불변하므로(w와 ^w가 이미 t-space에서 계산되었다고 가정) 유클리드 ray t-distance에 적용되거나 normalized ray s-distance에 적용되더라도 동일하게 동작한다.
우리는 NeRF 히스토그램(t, w)과 모든 제안 히스토그램(^t^k, ^w^k) 사이에 이 loss를 부과한다.
NeRF MLP는 mip-NeRF에서와 같이 입력 이미지 L_recon을 사용하여 재구성 loss를 사용하여 supervise됩니다.
우리는 L_prop를 계산할 때 NeRF MLP의 출력 t와 w에 정지 그래디언트를 두어 NeRF MLP가 "leads"하고 proposal MLP가 "follows"하도록 한다 - 그렇지 않으면 proposal MLP의 작업을 덜 어렵게 만들기 위해 NeRF가 현장의 더 나쁜 재구성을 생성하도록 장려될 수 있다.
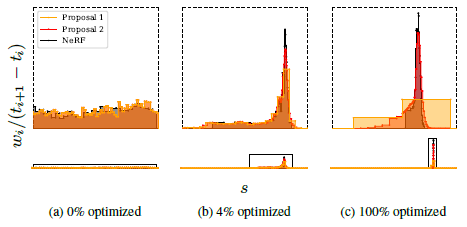
이 제안 supervision 효과는 그림 4에서 확인할 수 있는데, 여기서 proposal MLP는 NeRF 가중치를 포함하는 coarse 제안 히스토그램을 "catches up" 예측하는 동안 NeRF MLP는 장면의 표면 주위에 가중치를 점진적으로 로컬화한다.
4. Regularization for Interval-Based Models
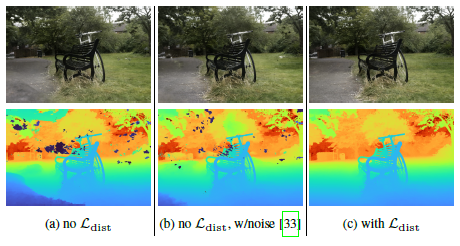
ill-posedness로 인해 학습된 NeRF는 종종 그림 5(a)에 표시된 "floaters"와 "background collapse"라고 부르는 두 가지 특징적인 아티팩트를 보여준다.
"floaters"에 의해 우리는 입력 뷰의 하위 집합의 일부 측면을 설명하는 역할을 하는 부피적으로 밀도가 높은 공간의 작은 분리된 영역을 의미하지만, 다른 각도에서 보면 블러 구름처럼 보인다.
"background collapse"란 먼 표면이 카메라에 가까운 밀도가 높은 콘텐츠의 반투명 구름으로 잘못 모델링되는 현상을 의미한다.
여기서는 그림 5와 같이 체적 밀도에 노이즈를 주입하는 NeRF가 사용하는 접근 방식보다 부유물과 배경 붕괴를 더 효과적으로 방지하는 정규화기를 제시한다[33].
우리의 정규화기는 각 ray를 매개 변수화하는 (normalized) ray 거리 s와 가중치 w의 집합에 의해 정의된 스텝 함수의 관점에서 간단한 정의를 가지고 있다:
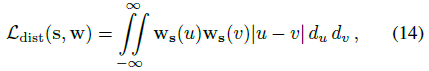
, 여기서 w_s(u)는 u: w_s(u) = ∑_i ω_i 1_[s_i, s_(i+1)) (u)에서 (s, w)에 의해 정의된 스텝 함수에 대한 보간이다.
t를 사용하면 거리 간격이 크게 가중되고 주변 간격이 효과적으로 무시되기 때문에 표준화된 ray 거리를 사용한다.
이 loss는 NeRF MLP에 의해 각 포인트에 할당된 가중치 w에 의해 스케일링된 이 1D 스텝 함수를 따라 모든 포인트 쌍 사이의 거리의 적분이다.
우리는 이것을 "distortion"이라고 부른다, 왜냐하면 이것은 k-means에 의해 최소화되는 왜곡의 연속적인 버전과 유사하기 때문이다(일종의 자기 상관을 최대화하는 것으로 생각할 수도 있지만).
이 loss는 w = 0(w 합계가 정확히 1이 아닌 1을 초과하지 않음)으로 설정하면 최소화됩니다.
그것이 가능하지 않은 경우(즉, ray가 비어 있지 않은 경우)에는 가중치를 가능한 작은 영역으로 통합하여 최소화한다.
그림 6은 toy 히스토그램에서 이 loss의 그래디언트를 보여줌으로써 이러한 동작을 보여줍니다.
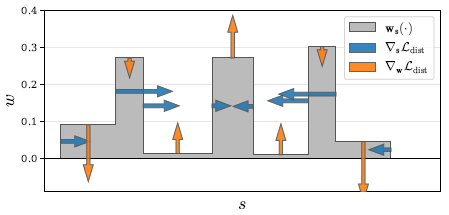
식 14는 정의하기 쉽지만 계산하기는 간단하다.
그러나 w_s(·)는 각 구간 내에서 일정한 값을 가지기 때문에 식 14를
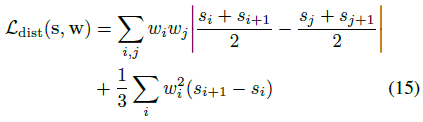
로 다시 쓸 수 있다.
이 형태에서, 우리의 왜곡 loss는 계산하기에 사소한 것이다.
이 재구성은 또한 이 loss가 어떻게 동작하는지에 대한 약간의 직관을 제공한다: 첫 번째 항은 모든 간격 중간점 쌍 사이의 가중 거리를 최소화하고 두 번째 항은 각 개별 간격의 가중 크기를 최소화한다.
5. Optimization
모델 구성 요소를 일반적인 항으로 설명했으므로 모든 실험에 사용되는 특정 모델을 자세히 설명할 수 있습니다.
우리는 4개의 레이어와 256개의 숨겨진 유닛을 가진 proposal MLP와 8개의 레이어와 1024개의 숨겨진 유닛을 가진 NeRF MLP를 사용하며, 둘 다 ReLU 내부 활성화와 밀도 τ에 대한 소프트플러스 활성화를 사용한다.
proposal MLP의 두 가지 평가 및 재샘플링을 각각 64개의 샘플을 사용하여(^s^0, ^w^0)와 (^s^1, ^w^1) 그리고 32개의 샘플을 사용하여 (s, w) NeRF MLP의 한 가지 평가 단계를 수행한다.
우리는 다음 loss를 최소화한다:
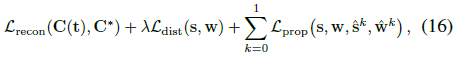
, 각 배치의 모든 ray에 대해 평균화된다(ray는 우리의 표기법에 포함되지 않는다).
λ 하이퍼 매개 변수는 데이터 항 L_recon과 정규화기 L_dist의 균형을 잡습니다.
우리는 모든 실험에서 λ = 0.01을 설정합니다.
L_prop에 사용되는 정지 그래디언트는 Θ_NeRF의 최적화와 독립적으로 Θ_prop의 최적화를 수행하므로 L_prop의 효과를 확장하기 위한 하이퍼 파라미터가 필요하지 않다.
L_recon의 경우, 우리는 ε = 0.001과 함께 Charbonnier loss [10]: √((x - x*)^2 + ε ^2)를 사용하며, 이는 mip-NeRF에 사용되는 평균 제곱 오차보다 약간 더 안정적인 최적화를 달성한다.
우리는 mip-NeRF의 학습 일정의 약간 수정된 버전을 사용하여 우리의 모델(및 보고된 모든 NeRF-like 베이스라인)을 학습한다.
배치 크기가 2^14인 Adam [24]을 사용하여 512번의 반복의 warm-up 단계와 10^-3의 표준으로 그래디언트 클리핑으로 2x10^3에서 2x10^-5로 어닐링되는 학습 속도인 β_1 = 0.99, β_2 = 0.999, ε = 10^-6을 사용하여 250k의 최적화를 반복한다.
6. Results
우리는 새로운 데이터 세트에서 우리의 모델을 평가합니다: 9개의 장면(옥외 5개, 실내 4개)은 각각 복잡한 중심 물체 또는 영역과 상세한 배경을 포함합니다.
캡처 중에 카메라 노출 설정을 고정하고 조명 변화를 최소화하며 움직이는 물체를 피하여 광도 변화를 방지하고자 했습니다 — 우리는 "in the wild" 사진 모음 [30]에 의해 제시되는 모든 과제를 조사할 의도는 없으며, 단지 스케일만을 조사할 뿐입니다.
카메라 포즈는 NeRF에서와 같이 COLMAP [45]을 사용하여 추정됩니다.
자세한 내용은 부록을 참조하십시오.
Compared methods.
우리는 모델을 NeRF [33] 및 mip-NeRF [3]과 비교하며, 두 모델 모두에서 사용되는 좌표 공간 내부의 전체 장면을 바인딩하기 위해 추가 위치 인코딩 주파수를 사용합니다.
우리는 두 개의 MLP를 사용하여 각 장면의 "inside"와 "outside"를 개별적으로 인코딩하는 NeRF++ [51]에 대해 평가합니다.
또한 로그 공간 샘플 및 자체와 다른 수축을 사용하는 DONeRF의 [34] 장면 매개 변수화를 사용하는 NeRF 버전에 대해 평가합니다.
또한 각 모델의 기본이 되는 MLP(s)가 매개 변수 수 측면에서 우리 모델과 대략 일치하도록 확장된 mip-NeRF 및 NeRF++ 변종 (mip-NeRF의 경우 숨겨진 단위 1024개, NeRF++의 경우 MLP 모두 512개)에 대해 평가합니다.
신경망이 외부 장면에 대해 학습되고 structure-from-motion [45]에 의해 생성된 프록시 기하학과 결합되는 다른 뷰 합성 패러다임의 SOTA 상태를 나타내는 non-NeRF 모델인 Stable View Synthesis [41]에 대해 평가합니다.
또한 외부 프록시 기하학에 의존하는 두 가지 실시간 IBR 기반 뷰 합성 접근 방식인 Deep Blending [17] 및 Point-Based Neural Rendering [26]의 공개적으로 사용 가능한 SIBR 구현 [7]과 비교합니다.
또한 장면 캡처 중 일관되지 않은 조명 조건으로 인해 발생하는 아티팩트를 개선하는 NeRF-W [6, 30]에 제시된 잠재적 외관 임베딩(4차원)을 사용하는 자체 모델의 변형을 제시합니다.
Comparative evaluation.
표 1에서는 데이터 세트의 테스트 이미지 전반에 걸쳐 평균 PSNR, SSIM [49] 및 LPIPS [52]를 보고합니다.
모든 NeRF-like 모델의 경우, 모델 크기뿐만 아니라 32개 코어 [20]를 가진 TPU v2로부터의 학습 시간도 보고합니다(SVS, Deep Blending 및 Point-Based Neural Rendering의 학습 시간 및 모델 크기는 이 비교가 특별히 의미가 없기 때문에 제시되지 않습니다).
우리의 모델은 모든 이전 NeRF-like 모델을 상당한 차이로 능가하며, 학습 시간이 2.17배 증가하여 mip-NeRF에 비해 평균 제곱 오차가 57% 감소했습니다.
더 큰 MLP를 사용하는 mip-NeRF 및 NeRF++ 베이스라인은 더 경쟁력이 있지만 모델보다 학습 속도가 ~3배 느리고 정확도가 현저히 낮습니다.
우리의 모델은 모든 오류 메트릭에서 Deep Blending 및 Point-Based Neural Rendering을 능가합니다.
또한 PSNR 및 SSIM의 SVS보다 성능이 뛰어나지만 LPIPS는 그렇지 않습니다.
이는 SVS가 LPIPS-like perceptual loss를 직접 최소화하는 동시에 픽셀당 재구성 loss를 최소화하도록 supervise되기 때문일 수 있습니다.
이미지 품질이 떨어졌음에도 불구하고 모델보다 낮은 LPIPS 점수를 달성하는 SVS의 렌더링 부록을 참조하십시오.
우리의 모델은 이미지 품질뿐만 아니라 SVS 및 Deep Blending 비해 몇 가지 장점이 있습니다: 이러한 모델은 외부 학습 데이터가 필요한 반면, 모델은 외부 학습 데이터가 필요하지 않으며, 모델은 MVS 패키지에 의해 생성된 프록시 기하학적 구조가 필요하지 않은 반면, 모델은 매우 상세한 depth 맵을 생성하지만, SVS 및 Deep Blending은 그렇지 않습니다(우리가 보여주는 "SVS depth"는 COLMAP [45]에 의해 생성되었으며 모델에 대한 입력으로 사용됨).
그림 7은 모델 출력을 보여주지만, 독자가 보충 비디오를 볼 수 있도록 권장합니다.
Ablation study.
표 2에서는 데이터 세트의 bicycle 장면에 대한 모델의 ablation 연구를 제시하며, 이 결과를 여기서 요약합니다.
A) L_prop을 제거하면 proposal MLP가 학습 중에 supervise되지 않기 때문에 성능이 크게 저하됩니다.
B) L_dist를 제거하면 메트릭에 실질적인 영향을 미치지 않지만 그림 5와 같이 장면 기하학에서 "floater" 아티팩트가 발생합니다.
C) 밀도에 가우시안 노이즈 (σ = 1)를 주입하는 Mildenhall et al. [33]이 제안한 정규화는 성능을 저하시킵니다(그림 5에서와 같이 플로터 제거에 덜 효과적입니다).
D) proposal MLP를 제거하고 단일 MLP를 사용하여 장면과 proposal 가중치를 모두 모델링하면 성능이 저하되지 않지만 학습 시간이 ~3배 증가하므로 작은 proposal MLP를 사용할 수 있습니다.
E) proposal MLP를 제거하고 mip-NeRF의 접근 방식(L_prop 대신 L_recon을 모든 coarse 척도로 적용)을 사용하여 모델을 학습시키면 속도와 정확성이 모두 악화되어 supervision 전략이 정당화됩니다.
F) 소형 NeRF MLP(1024개의 히든 유닛 대신 256개의 히든 유닛)를 사용하면 학습은 가속화되지만 품질은 저하되므로 세부 장면을 처리할 때 대용량 모델의 가치를 입증할 수 있습니다.
G) IPE를 완전히 제거하고 NeRF의 위치 인코딩[33]을 사용하면 성능이 저하되어 NeRF 대신 mip-NeRF를 기반으로 구축하는 값이 표시됩니다.
H) 축소를 완화하고 대신 위치 인코딩 주파수를 추가하여 장면을 바인딩하면 정확도와 속도가 저하됩니다.
I) DONeRF [34]에 제시된 파라미터화 및 로그 ray-spacing을 사용하면 정확도가 줄어듭니다.
Limitations.
mip-NeRF 360은 mip-NeRF와 다른 이전 작업보다 성능이 월등히 뛰어나지만 완벽하지는 않다.
bicycle 장면의 타이어 스포크(그림 5) 또는 stump 장면의 잎맥(그림 7)과 같이 일부 얇은 구조와 미세한 디테일이 누락될 수 있습니다.
카메라를 장면 중심에서 멀리 이동하면 뷰 합성 품질이 저하될 수 있습니다.
또한 대부분의 NeRF-like 모델과 마찬가지로 장면을 복구하려면 장치 내 학습을 제외하고 몇 시간의 가속기 학습이 필요합니다.
7. Conclusion
우리는 제약 없는 카메라 방향이 있는 실제 장면을 위해 설계된 mip-NeRF 확장인 mip-NeRF 360을 제시했다.
새로운 Kalman-like 장면 매개 변수화, 효율적인 proposal 기반 coarse-to-fine distillation 프레임워크 및 mip-NeRF ray 간격을 위해 설계된 정규화기를 사용하여, 우리는 mip-NeRF에 비해 평균 제곱 오차가 57% 감소하면서 무한 실제 장면에 도전하기 위해 현실적인 새로운 뷰와 복잡한 depth 맵을 합성할 수 있다.