2024. 6. 22. 13:48ㆍView Synthesis
Mip-Splatting: Alias-free 3D Gaussian Splatting
Zehao Yu, Anpei Chen, Binbin Huang, Torsten Sattler, Andreas Geiger
Abstract
최근 3D Gaussian Splatting은 인상적인 새로운 뷰 합성 결과를 보여주어 높은 충실도와 효율성에 도달했습니다.
그러나 샘플링 속도를 변경할 때 예를 들어 초점 거리나 카메라 거리를 변경하여 강력한 아티팩트를 관찰할 수 있습니다.
저희는 이 현상의 원인이 3D 주파수 제약의 부족과 2D 확장 필터의 사용에 기인할 수 있음을 발견했습니다.
이 문제를 해결하기 위해 입력 뷰에 의해 유도된 최대 샘플링 주파수를 기반으로 3D Gaussian 원시의 크기를 제한하는 3D 평활 필터를 도입하여 확대할 때 고주파 아티팩트를 제거합니다.
또한 2D 확장을 2D 박스 필터를 시뮬레이션하는 2D Mip 필터로 대체하면 앨리어싱 및 확장 문제를 효과적으로 완화할 수 있습니다.
단일 스케일 이미지에 대한 학습 및 여러 스케일에 대한 테스트와 같은 시나리오를 포함한 평가는 접근 방식의 효과를 검증합니다.
1. Introduction
Novel View Synthesis (NVS)은 가상 현실, 촬영, 로봇 공학 등을 포함한 다양한 응용 분야와 함께 컴퓨터 그래픽 및 컴퓨터 비전에서 중요한 역할을 합니다.
이 분야에서 특히 중요한 발전은 2020년 Mildenhall et al.이 도입한 Neural Radiance Field (NeRF) [28]입니다.
NeRF는 multi-layer perceptron (MLP)을 활용하여 지오메트리와 뷰 의존적 외관을 효과적으로 표현하여 놀라운 새로운 뷰 렌더링 품질을 보여줍니다.
최근에는 3D Gaussian Splatting (3DGS)[18]이 MLP [28]과 피처 그리드 기반 표현 [4, 11, 24, 32, 46]의 매력적인 대안으로 주목받고 있습니다.
3DGS는 고해상도에서 실시간 렌더링을 달성하면서 인상적인 새로운 뷰 합성 결과가 돋보입니다.
이러한 효율성과 효율성은 GPU의 표준 래스터화 파이프라인으로의 잠재적 통합과 함께 NVS 방법의 실제 사용을 향한 중요한 단계입니다.

구체적으로, 3DGS는 복잡한 장면을 3D Gaussians 세트로 나타내며, 이는 splatting 기반 래스터화를 통해 스크린 공간으로 렌더링됩니다.
각 3D Gaussian의 속성, 즉 위치, 크기, 방향, 불투명도 및 색상은 멀티 뷰 photometric loss를 통해 최적화됩니다.
그 후 저역 통과 필터링을 위해 스크린 공간에 2D 확장 작업이 적용됩니다.
3DGS는 인상적인 NVS 결과를 보여주었지만, 그림 1과 같이 카메라 뷰가 학습 중에 볼 수 있는 것과 다른 경우에 아티팩트를 생성합니다.
우리는 이 현상의 원인이 3D 주파수 제약 조건의 부족과 2D 확장 필터의 사용에 기인할 수 있음을 발견했습니다.
구체적으로, 줌아웃은 스크린 공간에서 투영된 2D Gaussians의 크기를 줄이는 반면, 동일한 양의 확장을 적용하면 확장 아티팩트가 발생합니다.
반대로, 줌인은 투영된 2D Gaussians이 확장되기 때문에 erosion 아티팩트를 유발하지만, 팽창이 일정하게 유지되어 2D 투영에서 Gaussians 간의 잘못된 간격이 발생합니다.
이러한 문제를 해결하기 위해 저희는 3D 공간에서 3D 표현을 정규화할 것을 제안합니다.
저희의 핵심 통찰력은 3D 장면을 재구성할 수 있는 최고 주파수가 본질적으로 입력 이미지의 샘플링 속도에 의해 제한된다는 것입니다.
저희는 먼저 Nyquist-Shannon Sampling Theorem [33, 45]에 따라 학습 뷰를 기반으로 각 Gaussian 원시의 멀티뷰 주파수 경계를 도출합니다.
최적화 중에 3D 공간의 3D Gaussian 원시에 저역 필터를 적용하여 Nyquist 한계를 충족하도록 3D 표현의 최대 주파수를 효과적으로 제한합니다.
학습 후 이 필터는 장면 표현의 intrinsic 부분이 되어 시점 변화에 관계없이 일정하게 유지됩니다.
결과적으로 저희의 방법은 그림 2의 8배 고해상도 이미지와 같이 확대할 때 3DGS [18]에 표시된 아티팩트를 제거합니다.

그럼에도 불구하고, 재구성된 장면을 더 낮은 샘플링 속도(예: 줌아웃)로 렌더링하면 앨리어싱이 발생합니다.
이전 작업 [1–3, 17]에서는 cone tracing을 사용하고 입력 위치 또는 피쳐 인코딩에 사전 필터링을 적용하여 앨리어싱을 다루며, 이는 3DGS에는 적용할 수 없습니다.
따라서 다양한 스케일에서 앨리어스-프리 재구성 및 렌더링을 보장하도록 특별히 설계된 2D Mip 필터('a la "mipmap")를 도입합니다.
우리의 2D Mip 필터는 2D Gaussian 저역 통과 필터로 근사하여 실제 물리 이미징 프로세스에 고유한 2D 박스 필터를 모방합니다 [29, 37, 48].
멀티 스케일 이미지로 학습하는 동안 멀티 스케일 신호를 보간하는 MLP의 기능에 의존하는 이전 작업 [1–3, 17]과 달리, 3D Gaussian 표현에 대한 폐쇄형 수정은 우수한 분포 외 일반화를 초래합니다: 단일 샘플링 속도로 학습하면 그림 2의 1/4배 다운 샘플링된 이미지에서 알 수 있듯이 학습 중에 사용되는 것과는 다른 다양한 샘플링 속도로 충실한 렌더링이 가능합니다.
요약하면, 우리는 다음과 같은 기여를 합니다:
• 우리는 3DGS용 3D 스무딩 필터를 도입하여 3D Gaussian 원시의 최대 주파수를 효과적으로 정규화하여 이전 방법의 분산 외 렌더링에서 관찰된 아티팩트를 해결합니다[18, 59].
• 앨리어싱 및 확장 아티팩트를 해결하기 위해 2D 확장 필터를 2D Mip 필터로 교체합니다.
• 까다로운 벤치마크 데이터 세트에 대한 실험 [2, 28]은 샘플링 속도를 수정할 때 Mip-Splating의 효과를 보여줍니다.
• 우리의 3DGS 수정은 원칙적이고 간단하여 원래 3DGS 코드를 거의 변경하지 않아도 됩니다.
2. Related Work
Novel View Synthesis: NVS는 원본 캡처 [12, 22]와 다른 관점에서 새로운 이미지를 생성하는 프로세스입니다.
볼륨 렌더링 [10, 21, 25, 26]을 활용하는 NeRF [28]은 이 분야의 표준 기술이 되었습니다.
NeRF는 MLP [5, 27, 34]를 활용하여 장면을 연속 함수로 모델링합니다, 이는 간결한 표현에도 불구하고 각 ray 점에 필요한 값비싼 MLP 평가로 인해 렌더링 속도를 저해합니다.
후속 방법 [16, 40, 41, 52, 54]은 사전 학습된 NeRF를 희소 표현으로 distill하여 NeRF의 실시간 렌더링을 가능하게 합니다.
고급 장면 표현으로 NeRF의 학습 및 렌더링을 개선하기 위해 추가 발전이 이루어졌습니다 [4, 6, 11, 18, 19, 24, 32, 46, 51].
특히 3D Gaussians Splatting (3DGS) [18]은 고화질 해상도에서 실시간 렌더링을 달성하면서 인상적인 새로운 뷰 합성 결과를 보여주었습니다.
중요한 것은 3DGS가 장면을 3D Gaussians의 모음으로 명시적으로 표현하고 ray 트레이싱 대신 래스터화를 사용한다는 것입니다.
그럼에도 불구하고 3DGS는 유사한 샘플링 속도(초점 길이/장면 거리)에서 학습과 테스트가 수행되는 분포 내 평가에 중점을 둡니다.
이 논문에서는 3DGS의 분포 외 일반화를 연구하고 단일 스케일에서 모델을 학습하고 멀티 스케일에서 평가합니다.
Primitive-based Differentiable Rendering: 지오메트릭 원시를 이미지 평면에 래스터화하는 원시 기반 렌더링 기술은 효율성 때문에 광범위하게 연구되어 왔습니다[13, 14, 38, 44, 59, 60].
미분가능한 포인트 기반 렌더링 방법 [20, 36, 39, 43, 49, 53, 57]은 복잡한 구조를 표현하는 데 큰 유연성을 제공하므로 새로운 뷰 합성에 적합합니다.
특히 Pulsar [20]는 효율적인 구 래스터화가 돋보입니다.
최근의 3D Gaussian Splatting (3DGS) 작업 [18]은 anisotropic Gaussians [59]을 활용하고 렌더링을 위해 타일 기반 정렬을 도입하여 놀라운 프레임 속도를 달성합니다.
인상적인 결과에도 불구하고 3DGS는 다른 샘플링 속도로 렌더링할 때 강력한 아티팩트를 나타냅니다.
저희는 3D Gaussian 원시 표현의 최대 주파수를 제한하는 3D 스무딩 필터와 앨리어스-프리 렌더링을 위해 물리적 이미징 프로세스의 상자 필터를 근사화하는 2D Mip 필터를 도입하여 이 문제를 해결합니다.
Anti-aliasing in Rendering: 앨리어싱을 방지하기 위한 두 가지 주요 전략이 있습니다: 샘플 수를 늘리는 슈퍼 샘플링 [7]과 나이퀴스트 제한 [8, 15, 31, 47, 50, 59]을 충족하기 위해 신호에 저역 통과 필터링을 적용하는 프리필터링입니다.
예를 들어, EWA splatting [59]은 스크린 공간에서 투영된 2D Gaussian에 Gaussian 저역 통과 필터를 적용하여 이미지의 나이퀴스트 주파수를 존중하는 대역 제한 출력을 생성합니다.
또한 Gaussian 원시에 대역 제한 필터를 적용하는 반면, 밴드 제한 필터는 3D 공간에 적용되며 필터 크기는 렌더링할 이미지가 아닌 학습 이미지에 의해 완전히 결정됩니다.
우리의 2D Mip 필터도 스크린 공간에서 Gaussian 저역 통과 필터이지만 물리적 이미징 프로세스의 박스 필터에 근사하여 단일 픽셀에 가깝습니다.
반대로 EWA 필터는 주파수 신호의 대역폭을 렌더링된 이미지로 제한하고 필터의 크기는 경험적으로 선택됩니다.
[59]의 중요한 차이점은 재구성 문제를 해결한다는 것인데, 이는 역 렌더링을 통해 3D Gaussian 표현을 최적화하는 반면 EWA splatting은 렌더링 문제만 고려한다는 것입니다.
최근의 신경 렌더링 방법은 사전 필터링을 통합하여 앨리어싱을 완화합니다 [1–3, 17, 58].
예를 들어 Mip-NeRF [1]는 고주파 세부 정보를 감쇠시키기 위해 integrated position encoding (IPE)을 도입했습니다.
유사한 아이디어가 피쳐 그리드 기반 표현을 위해 채택되었습니다 [3, 17, 58].
그러나 이러한 접근 방식은 supervision을 위해 멀티 스케일 이미지가 필요합니다.
대조적으로, 우리의 접근 방식은 3DGS [18]를 기반으로 하며 픽셀 크기를 기반으로 필요한 저역 통과 필터 크기를 결정하여 학습 중에 관찰되지 않는 규모에서 앨리어스-프리 렌더링을 허용합니다.
3. Preliminaries
이 섹션에서는 먼저 섹션 3.1의 샘플링 정리를 검토하여 앨리어싱 문제를 이해하기 위한 기반을 마련합니다.
이어서 섹션 3.2에서 3D Gaussian Splatting (3DGS) [18]과 그 렌더링 프로세스를 소개합니다.
3.1. Sampling Theorem
샘플링 정리는 Nyquist-Shannon Sampling Theorem [33, 45]라고도 하며, 연속적인 신호가 이산 샘플로부터 정확하게 표현되거나 재구성될 수 있는 조건을 설명하는 신호 처리 및 디지털 통신의 기본 개념입니다.
정보의 손실 없이 이산 샘플로부터 연속적인 신호를 정확하게 재구성하려면 다음 조건이 충족되어야 합니다:
Condition 1 연속 신호는 대역 제한이 있어야 하며 특정 최대 주파수 ν 이상의 주파수 성분을 포함하지 않을 수 있습니다.
Condition 2 샘플링 속도 ˆν은 연속 신호에 존재하는 최고 주파수의 두 배 이상이어야 합니다: ˆν ≥ 2ν
.
실제로 이산 샘플에서 신호를 재구성할 때 제약 조건을 만족시키기 위해 저역 통과 또는 안티 앨리어싱 필터가 샘플링 전에 신호에 적용됩니다.
필터는 ˆν/2 이상의 주파수 성분을 제거하고 앨리어싱으로 이어질 수 있는 고주파 콘텐츠를 감쇠시킵니다.
3.2. 3D Gaussian Splatting
이전 연구 [18, 59]에서는 3D 장면을 스케일된 3D Gaussian 원시 {G_k|k = 1, ···, K} 집합으로 표현하고 볼륨 splatting을 사용하여 이미지를 렌더링할 것을 제안합니다.
스케일된 각 3D Gaussian G_k의 지오메트리는 월드 스페이스에서 정의된 불투명도 (스케일) α_k ∈ [0, 1], 중심 p_k ∈ R^(3×1) 및 공분산 행렬 ∑_k ∈ R^(3×3)에 의해 매개변수화됩니다:
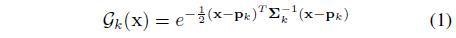
∑_k를 유효한 공분산 행렬의 공간으로 제한하기 위해 semi-definite 매개변수화 ∑_k = O_k s_k s_k^T O_k^T가 사용됩니다.
여기서 s ∈ R^3은 스케일링 벡터이고 O ∈ R^(3x3)은 회전 행렬로, 쿼터니언으로 매개변수화됩니다[18].
회전 R ∈ R^(3x3) 및 변환 t ∈ R^3에 의해 정의된 특정 시점에 대한 이미지를 렌더링하려면 먼저 3D Gaussians {G_k}을 카메라 좌표로 변환합니다:
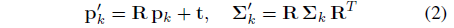
그런 다음 로컬 아핀 변환
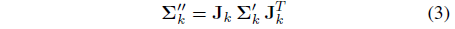
을 통해 ray 공간에 투영되며, 여기서 자코비안 행렬 J_k는 3D 가우시안 p'_k의 중심에 의해 정의된 투영 변환에 대한 아핀 근사치입니다.
∑'_k의 세 번째 행과 열을 건너뛰면 ray 공간에서 2D 공분산 행렬 ∑_k^2D를 얻고 G_k^2D를 사용하여 해당 스케일링된 2D Gaussian을 참조하여 자세한 내용은 [18]을 참조하십시오.
마지막으로, 3DGS [18]는 구면 고조파를 사용하여 뷰 종속 색상 c_k를 모델링하고 원시의 깊이 순서 1, ...,K에 따라 알파 블렌딩을 통해 이미지를 렌더링합니다:
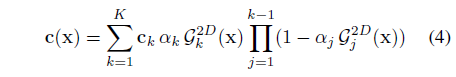
Dilation: 투영된 2D Gaussian이 스크린 공간에서 너무 작은 경우, 즉 픽셀보다 작은 경우를 방지하기 위해 투영된 2D Gaussian은 다음과 같이 확장됩니다:
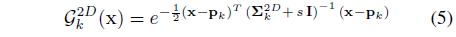
, 여기서 I는 2D 항등 행렬이고 s는 스칼라 팽창 하이퍼파라미터입니다.
이 연산자는 최대치를 그대로 두면서 2D Gaussian의 스케일을 조정합니다.
이 효과는 형태학적으로 팽창 연산자와 비슷하기 때문에 우리는 이것을 2D 스크린 공간 팽창 연산이라고 불렀습니다.
Reconstruction: 렌더링 프로세스가 빠르고 미분 가능하기 때문에 멀티뷰 loss를 사용하여 3D Gaussian 파라미터를 효율적으로 최적화할 수 있습니다.
최적화하는 동안 3D Gaussians은 장면을 더 잘 표현하기 위해 적응적으로 추가되고 삭제됩니다.
자세한 내용은 [18]을 참조하십시오.
4. Sensitivity to Sampling Rate
전통적인 순방향 splatting에서는 Gaussian 원시의 중심 p_k와 색상 c_k가 미리 결정되는 반면, 3D Gaussian 공분산 ∑_k는 경험적으로 선택됩니다 [42, 59].
반면, 3DGS [18]는 멀티뷰 photometric loss를 역전파하여 역 렌더링 프레임워크를 통해 모든 매개변수를 공동으로 최적화합니다.
저희는 이 최적화가 하나의 객체와 5개의 픽셀을 가진 이미지 센서를 포함하는 간단한 예를 보여주는 그림 1과 같은 모호성으로 인해 어려움을 겪는다는 것을 관찰했습니다.
(a)의 3D 객체, 3D Guassian에 의한 근사치 및 화면 공간 (파란색 픽셀)으로의 투영을 고려합니다.
Gaussian 커널(크기 ≈ 1 픽셀)을 사용한 화면 공간 확장 (식. 5)으로 인해 (b)의 디랙 δ 함수로 표현되는 퇴화된 3D Gaussian은 유사한 이미지로 이어집니다.
이는 3D Gaussian의 규모가 적절하게 제한되지 않는다는 것을 보여줍니다.
실제로 3DGS는 암묵적인 수축 편향으로 인해 최적화 중에 실제로 3D Gaussian의 규모 매개변수를 체계적으로 과소평가합니다.
이는 유사한 샘플링 속도로 렌더링하는 데 영향을 미치지 않지만(cf. 그림 1 (a) vs. (b)) 카메라를 확대하거나 더 가까이 이동할 때 침식 효과를 초래합니다.
이는 확장된 2D Gaussians이 화면 공간이 작아지기 때문입니다.
이 경우 렌더링된 이미지는 고주파 아티팩트를 나타내어 그림 1 (d)에 표시된 것처럼 실제보다 얇은 객체 구조를 렌더링합니다.
반대로 화면 공간 확장은 (a)의 줌 아웃 버전을 보여주는 그림 1 (c)와 같이 샘플링 속도를 감소시킬 때 렌더링에도 부정적인 영향을 미칩니다.
이 경우 확장은 radiance를 여러 픽셀에 걸쳐 물리적으로 잘못된 방식으로 확산시킵니다.
(c)에서 3D 물체의 투영에 의해 덮인 영역은 픽셀보다 작지만 확장된 Gaussian은 감쇠되지 않아 픽셀에 도달하는 것보다 더 많은 빛을 축적합니다.
이는 증가된 밝기와 확장 아티팩트로 이어져 자전거 바퀴의 스포크의 외관을 크게 저하시킵니다.
앞서 언급한 스케일 모호성은 수백만의 Gaussains을 포함하는 표현에서 특히 문제가 됩니다.
그러나 단순히 화면 공간 확장을 폐기하면 Mip-NeRF 360 데이터 세트 [2]에 존재하는 것과 같은 복잡한 장면에 대한 최적화 문제가 발생하며, 여기서 밀도 제어 메커니즘에 의해 많은 수의 작은 Gaussians이 생성되어 GPU 용량을 초과합니다[18].
또한 모델을 확장하지 않고 성공적으로 학습할 수 있더라도 샘플링 속도를 줄이면 안티 앨리어싱이 부족하여 앨리어싱 효과가 발생합니다 [59].
5. Mip Gaussian Splatting
이러한 문제를 극복하기 위해 원래 3DGS 모델을 두 가지 수정합니다.
특히 3D 표현의 주파수를 학습 이미지에 의해 결정된 최대 샘플링 속도의 절반 이하로 제한하여 확대할 때 고주파 아티팩트를 제거하는 3D 스무딩 필터를 도입합니다.
또한 2D 화면 공간 확장을 물리적 이미징 프로세스에 고유한 박스 필터에 근사하고 앨리어싱 및 확장 문제를 효과적으로 완화하는 2D Mip 필터로 대체하는 것을 보여줍니다.
이를 함께 사용하면 Mip-Splatting을 통해 다양한 샘플링 속도에서 앨리어스-프리 렌더링이 가능합니다.
이제 3D 스무딩 필터와 2D Mip 필터에 대해 자세히 설명합니다.
5.1. 3D Smoothing Filter
멀티 뷰 관측에서 3D radiance field 재구성은 서로 뚜렷하게 다른 여러 재구성이 동일한 2D 투영을 초래할 수 있기 때문에 잘 알려져 있는 ill-posed 문제입니다 [2, 55, 56].
우리의 핵심 통찰력은 재구성된 3D 장면의 가장 높은 주파수가 학습 뷰에 의해 정의된 샘플링 속도에 의해 제한된다는 것입니다.
Nyquist’s theorem 3.1을 따라 최적화 중에 3D 표현의 최대 주파수를 제한하는 것을 목표로 합니다.
Multiview Frequency Bounds: 멀티뷰 이미지는 연속적인 3D 장면의 2D 투영입니다.
이산 이미지 그리드는 연속적인 3D 신호에서 포인트를 샘플링하는 위치를 결정합니다.
이 샘플링 속도는 본질적으로 이미지 해상도, 카메라 초점 거리 및 장면과 카메라로부터의 거리와 관련이 있습니다.
픽셀 단위로 초점 거리가 f인 이미지의 경우 스크린 공간의 샘플링 간격은 1입니다.
이 픽셀 간격이 3D world 공간에 역투영되면 주어진 depth d에서 world 공간 샘플링 간격 ˆT가 생성되고 샘플링 주파수 ˆν는 그 역으로 나타납니다:
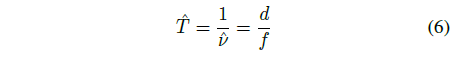
Nyquist's theorem 섹션 3.1에서 가정한 바와 같이, 주파수 ˆν에서 추출된 샘플이 주어지면, 재구성 알고리즘은 최대 ˆν/2, 또는 f/2d의 주파수를 가진 신호의 구성 요소를 재구성할 수 있습니다.
결과적으로, 2ˆT보다 작은 원시는 크기가 샘플링 간격의 두 배 미만이기 때문에, splatting 과정에서 앨리어싱 아티팩트가 발생할 수 있습니다.
단순화하기 위해 원시 p_k의 중심을 사용하여 depth d를 근사화하고 샘플링 간격 추정을 위해 폐색의 영향을 무시합니다.
원시의 샘플링 속도는 depth에 따라 다르며 카메라마다 다르기 때문에 원시 k에 대한 최대 샘플링 속도를
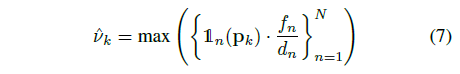
로 결정하고, 여기서 N은 이미지의 총 수이며, 1_n(p)는 원시의 가시성을 평가하는 지표 함수입니다.
Gaussian 중심 p_k가 n번째 카메라의 뷰 frustum 내에 해당하는 경우에는 사실입니다.
직관적으로 각 원시를 재구성할 수 있는 카메라가 하나 이상 존재하도록 샘플링 속도를 선택합니다.
이 프로세스는 N = 5에 대한 그림 3에 나와 있습니다.
구현에서는 3D Gaussians 중심이 학습 전반에 걸쳐 비교적 안정적으로 유지된다는 것을 발견했기 때문에 매 m번 반복할 때마다 각 Gaussians 원시의 최대 샘플링 속도를 다시 계산합니다.
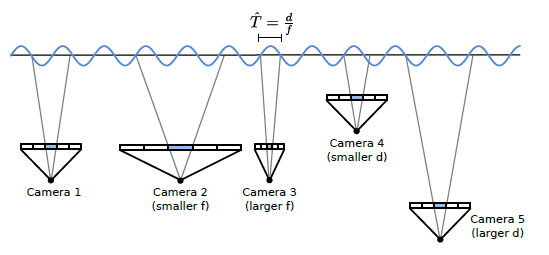
3D Smoothing: 원시에 대한 최대 샘플링 속도 ˆν_k가 주어지면 3D 표현의 최대 주파수를 제한하는 것을 목표로 합니다.
이는 스크린 공간에 투영하기 전에 Gaussian 저역 통과 필터 G_low를 각 3D Gaussian 원시 G_k에 적용함으로써 달성됩니다:
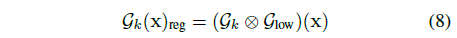
이 연산은 두 Gaussians을 공분산 행렬 ∑_1 및 ∑_2로 분해하면 분산 ∑_1 + ∑_2인 또 다른 Gaussian이 생성되므로 효율적입니다.
이런 이유로,
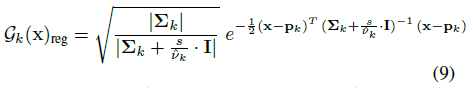
여기서 s는 필터의 크기를 제어하기 위한 스칼라 하이퍼파라미터입니다.
각 원시에 대한 3D 필터의 스케일 s/ˆν_k는 볼 수 있는 학습 뷰에 따라 다르기 때문에 다릅니다.
3D Gaussain 스무딩을 사용하여 Gaussian의 최고 주파수 성분이 적어도 하나의 카메라에 대한 최대 샘플링 속도의 절반을 초과하지 않도록 합니다.
G_low는 3D 표현의 intrinsic 부분이 되어 일정한 사후 학습을 유지합니다.
5.2. 2D Mip Filter
우리의 3D 스무딩 필터는 고주파 아티팩트 [18, 59]를 효과적으로 완화하지만, 재구성된 장면을 더 낮은 샘플링 속도로 렌더링(예: 줌아웃 또는 카메라를 더 멀리 이동)하면 여전히 앨리어싱으로 이어질 수 있습니다.
이를 극복하기 위해 3DGS의 화면 공간 확장 필터를 2D Mip 필터로 교체합니다.
보다 구체적으로, 저희는 카메라 센서의 픽셀을 타격하는 광자가 픽셀의 영역에 통합되는 물리적 이미징 프로세스를 복제합니다 [29, 37, 48].
이상적인 모델은 이미지 공간에서 2D 박스 필터를 사용하는 반면, 효율성
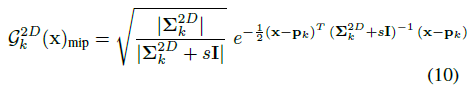
을 위해 2D Gaussian 필터로 근사화하며, 여기서 s는 스크린 공간에서 단일 픽셀을 덮도록 선택됩니다.
우리의 Mip 필터는 EWA 필터 [59]와 유사점을 공유하지만 기본 원리는 명확합니다.
우리의 Mip 필터는 단일 픽셀의 정확한 근사치를 타겟팅하여 이미징 프로세스에서 박스 필터를 복제하도록 설계되었습니다.
반대로 EWA 필터의 역할은 주파수 신호의 대역폭을 제한하는 것이며 필터의 크기는 경험적으로 선택됩니다.
EWA 논문 [15, 59]은 화면의 3x3 픽셀 영역을 효과적으로 차지하는 동일성 공분산 행렬을 옹호하기도 합니다.
그러나 이 접근 방식은 실험에서 보여줄 것처럼 축소할 때 지나치게 부드러운 결과를 가져옵니다.
6. Experiments
먼저 Mip-Splating의 구현 세부 사항을 제시합니다.
그런 다음 Blender 데이터 세트 [28]와 까다로운 Mip-NeRF 360 데이터 세트 [2]에서 성능을 평가합니다.
마지막으로 접근 방식의 한계에 대해 논의합니다.
6.1. Implementation
저희는 인기 있는 오픈 소스 3DGS 코드 기반을 기반으로 방법을 구축합니다 [18].
[18]에 이어 모든 장면에서 30K 반복을 위해 모델을 학습하고 동일한 loss 함수, Gaussain 밀도 제어 전략, 스케줄 및 하이퍼파라미터를 사용합니다.
효율성을 위해 매 m=100번 반복할 때마다 각 3D Gaussians의 샘플링 속도를 다시 계산합니다.
저희는 2D Mip 필터의 분산을 0.1, 대략 단일 픽셀, 3D 스무딩 필터의 분산을 0.2로 선택하여 3DGS [18] 및 3DGS + EWA [59]와 공정한 비교를 위해 총 0.3을 선택하여 3DGS의 확장을 EWA 필터로 대체합니다.
6.2. Evaluation on the Blender Dataset
Multi-scale Training and Multi-scale Testing: 이전 작업 [1, 17]에 이어 멀티 스케일 데이터로 모델을 학습하고 멀티 스케일 데이터에 대해 평가합니다.
저해상도 이미지에 비해 전체 해상도 이미지의 ray가 더 자주 샘플링되는 [1, 17]과 유사하게, 저희는 전체 해상도 이미지의 40%와 다른 이미지 해상도에서 각각 20%를 샘플링합니다.
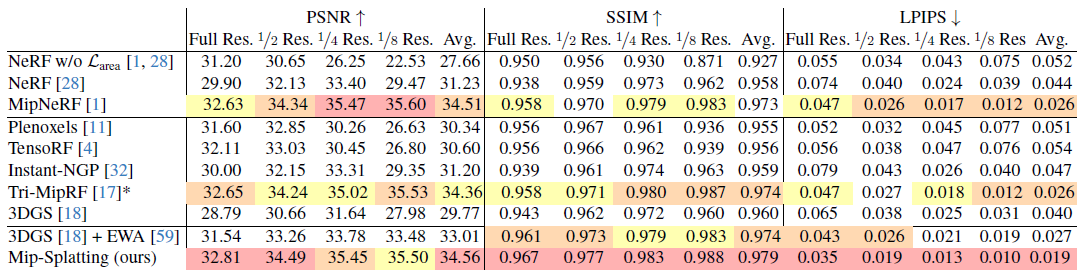
저희의 정량적 평가는 표 1에 나와 있습니다.
저희의 접근 방식은 Mip-NeRF [1] 및 Tri-MipRF [17]와 같은 SOTA 방법과 비교해도 비슷하거나 우수한 성능을 달성합니다.
특히 저희의 방법은 2D Mip 필터 덕분에 3DGS [18] 및 3DGS + EWA [59]를 상당한 차이로 능가합니다.
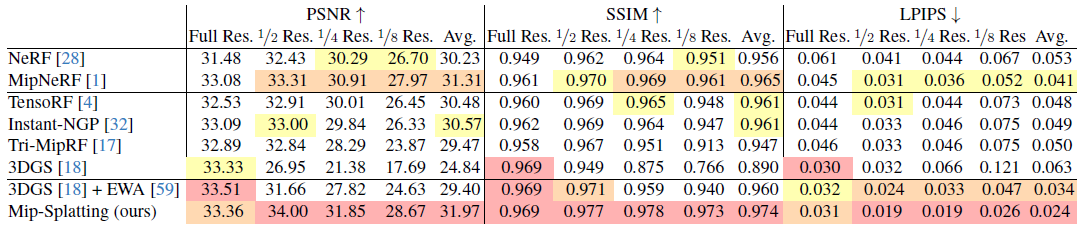
Single-scale Training and Multi-scale Testing: 단일 스케일 데이터로 학습된 모델을 동일한 규모로 평가하는 이전 작업과 달리, 저희는 줌아웃 효과를 모방하기 위해 전체 해상도 이미지에 대한 학습과 다양한 해상도(즉, 1x, 1/2, 1/4 및 1/8)의 렌더링을 포함하는 중요한 새로운 설정을 고려합니다.
이 설정에 대한 공개 벤치마크가 없는 경우, 저희는 모든 베이스라인 방법을 직접 학습했습니다.
저희는 효율성을 위해 NeRF [28], Instant-NGP [32] 및 TensoRF [4]에 NeRFAcc [23]의 구현을 사용합니다.
공식 구현은 Mip-NeRF [1], Tri-MipRF [17] 및 3DGS [18]에 사용되었습니다.
표 2에 제시된 정량적 결과는 저희 방법이 기존의 모든 SOTA 방법을 훨씬 능가한다는 것을 나타냅니다.
정성적 비교가 그림 4에 제공되어 있습니다.
3DGS [18] 기반 방법은 Mip-NeRF [1] 및 Tri-MipRF [17]보다 fine 디테일을 더 효과적으로 캡처하지만, 원래 학습 규모에서만 가능합니다.
특히, 저희 방법은 저해상도에서 렌더링 품질이 3DGS [18] 및 3DGS + EWA [59]를 모두 능가합니다.
특히, 3DGS [18]는 확장 아티팩트를 나타냅니다.
EWA splatting [59]은 큰 저역 통과 필터를 사용하여 렌더링된 이미지의 주파수를 제한하여 오버 스무딩된 이미지를 생성하며, 이는 특히 저해상도에서 분명해집니다.


6.3. Evaluation on the Mip-NeRF 360 Dataset
Single-scale Training and Multi-scale Testing: 줌인 효과를 시뮬레이션하기 위해 8배로 다운샘플링되고 연속적으로 더 높은 해상도(1배, 2배, 4배, 8배)로 렌더링된 데이터에 대해 모델을 학습합니다.
이 설정에 대한 공개 벤치마크가 없는 경우 모든 기본 방법을 직접 학습했습니다.
저희는 Mip-NeRF 360 [1] 및 3DGS [18]에 대한 공식 구현을 사용하고 Zip-NeRF [3]에 대한 커뮤니티 재구현을 사용합니다.
표 3의 결과는 저희의 방법이 학습 규모(1배)에서 이전 작업과 유사한 성능을 발휘하고 더 높은 해상도에서 모든 SOTA 방법을 훨씬 능가한다는 것을 보여줍니다.
그림 5에 표시된 바와 같이 저희의 방법은 고주파 아티팩트 없이 고충실도 이미지를 생성합니다.
특히, Mip-NeRF 360 [2]과 Zip-NeRF [3]은 모두 MLP가 분포 범위를 벗어난 주파수로 외삽할 수 없기 때문에 증가된 해상도에서 낮은 성능을 보입니다.
3DGS [18]는 확장 작업으로 인해 눈에 띄는 침식 아티팩트를 도입하지만 3DGS + EWA [59]는 뚜렷한 고주파 아티팩트를 생성하면서도 더 나은 성능을 발휘합니다.
대조적으로 저희의 방법은 이러한 아티팩트를 피하여 ground truth와 더 유사한 미적으로 만족스러운 이미지를 생성합니다.
더 높은 해상도로 렌더링하는 것은 초해상도 작업이며 모델은 학습 데이터에 없는 고주파 세부 정보를 환각해서는 안 된다는 점에 유의하는 것이 중요합니다.

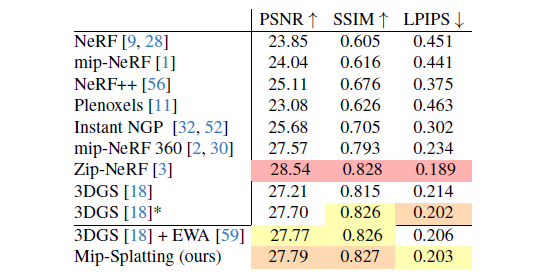
Single-scale Training and Same-scale Testing: 저희는 널리 사용되는 설정에 따라 Mip-NeRF 360 데이터 세트 [2]에서 저희 방법을 추가로 평가하는데, 여기서 모델은 동일한 규모로 학습되고 테스트되며 실내 장면은 2배, 실외 장면은 4배 다운샘플링됩니다.
표 4에서 볼 수 있듯이 저희 방법은 성능 저하 없이 이 까다로운 벤치마크에서 3DGS [18] 및 3DGS + EWA [59]와 동등한 성능을 발휘합니다.
이는 다양한 설정을 처리하는 저희 방법의 효율성을 확인시켜줍니다.
6.4. Limitations
저희의 방법은 효율성을 위해 박스 필터의 근사치로 Gaussian 필터를 사용합니다.
그러나 이 근사치는 특히 Gaussian이 화면 공간이 작을 때 오류를 발생시킵니다.
이 문제는 표 2에서 볼 수 있듯이 줌아웃이 증가하면 더 큰 오류가 발생하는 실험 결과와 관련이 있습니다.
또한 각 3D Gaussian에 대한 샘플링 속도를 m = 100번 반복할 때마다 계산해야 하기 때문에 학습 오버헤드가 약간 증가합니다.
현재 이 계산은 PyTorch [35]를 사용하여 수행되며 보다 효율적인 CUDA 구현은 잠재적으로 이러한 오버헤드를 줄일 수 있습니다.
샘플링 속도는 카메라 포즈와 고유성에만 의존하기 때문에 사전 계산 및 저장을 위한 더 나은 데이터 구조를 설계하는 것이 향후 작업을 위한 방법입니다.
앞서 언급했듯이 샘플링 속도 계산이 학습 중 유일한 전제 조건이며 3D 스무딩 필터는 식 9의 Gaussian 원시와 융합되어 렌더링 중에 추가 오버헤드를 제거할 수 있습니다.
7. Conclusion
저희는 임의의 스케일에서 앨리어스-프리 렌더링을 달성하기 위해 3D 스무딩 필터와 2D Mip 필터라는 두 가지 새로운 필터를 도입하는 3D Gaussian Splatting을 수정한 Mip-Splatting을 제시했습니다.
저희의 3D 스무딩 필터는 학습 이미지에 의해 부과된 샘플링 제약 조건과 일치하도록 Gaussian 원시의 최대 주파수를 효과적으로 제한하는 반면, 2D Mip 필터는 물리적 이미징 프로세스를 시뮬레이션하기 위해 박스 필터를 근사화합니다.
저희의 실험 결과는 Mip-Splatting이 동일한 스케일/샘플링 속도로 학습하고 테스트할 때 성능 측면에서 SOTA 방법과 경쟁력이 있음을 보여줍니다.
중요한 것은 학습과 다른 샘플링 속도로 테스트할 때 분포 외 시나리오에서 SOTA 방법을 훨씬 능가하여 분포 외 카메라 포즈와 줌 팩터에 대한 일반화가 더 잘 이루어진다는 것입니다.
'View Synthesis' 카테고리의 다른 글
| 3D Gaussian Splatting for Real-Time Radiance Field Rendering (0) | 2023.10.29 |
|---|---|
| Instruct-NeRF2NeRF: Editing 3D Scenes with Instructions (0) | 2023.09.29 |
| D-NeRF: Neural Radiance Fields for Dynamic Scenes (1) | 2023.09.04 |
| Instant Neural Graphics Primitives with a Multiresolution Hash Encoding (0) | 2023.08.16 |
| DynIBaR: Neural Dynamic Image-Based Rendering (0) | 2023.07.13 |