2022. 2. 11. 17:35ㆍ3D Vision
Volume Rendering of Neural Implicit Surfaces
Lior Yariv, Jiatao Gu, Yoni Kasten, Yaron Lipman
Abstract
신경 볼륨 렌더링은 희박한 입력 이미지 세트에서 장면의 새로운 뷰를 합성하는 데 성공했기 때문에 최근 인기가 높아지고 있다.
지금까지 신경용적 렌더링 기법으로 학습한 지오메트리는 일반밀도함수를 이용해 모델링했다.
또한 기하학 자체는 밀도 함수의 임의 수준 세트를 사용하여 추출되어 노이즈가 많고 종종 낮은 충실도의 재구성을 초래했다.
이 논문의 목표는 신경 볼륨 렌더링에서 지오메트리 표현 및 재구성을 개선하는 것이다.
우리는 부피 밀도를 기하학의 함수로 모델링함으로써 그것을 달성한다.
이것은 부피 밀도의 함수로 지오메트리를 모델링한 이전 작업과 대조됩니다.
더 자세히, 우리는 부피 밀도 함수를 부호 거리 함수(SDF) 표현에 적용되는 라플레이스의 누적 분포 함수(CDF)로 정의한다.
이 간단한 밀도 표현에는 세 가지 이점이 있습니다.
(i) 신경 용적 렌더링 프로세스에서 학습한 형상에 유용한 유도 바이어스를 제공한다.
(ii) 불투명도 근사 오류에 대한 경계를 용이하게 하여 정확한 가시광선 샘플링을 유도한다.
정확한 샘플링은 기하학적 구조와 광도의 정확한 결합을 제공하는 데 중요하다.
그리고 (iii) 볼륨 렌더링에서 모양과 외관의 효율적인 감독되지 않은 분리를 가능하게 한다.
도전적인 장면 멀티뷰 데이터 세트에 이 새로운 밀도 표현을 적용하면 관련 기준선을 능가하는 고품질 지오메트리 재구성이 생성되었다.
게다가, 두 장면의 분리로 인해 장면 사이의 모양과 외관이 전환될 수 있다.
1. Introduction
볼륨 렌더링 [22]은 볼륨 렌더링 적분으로 광도 필드의 볼륨 밀도를 렌더링하는 기술 집합입니다.
최근 밀도와 광도 필드를 모두 신경망으로 나타내는 것은 입력 이미지의 희박한 집합에서만 학습함으로써 새로운 관점을 훌륭하게 예측할 수 있는 것으로 나타났다.
[25]에 제시되고 후속[39, 3]에 의해 개발된 이 신경 볼륨 렌더링 접근법은 입력 이미지에서 동시에 학습할 수 있는 다른 방식으로 알파 합성으로서의 적분을 근사화한다.
이러한 결합이 새로운 보기 방향의 우수한 일반화로 이어지기는 하지만 밀도 부분은 장면의 실제 형상을 충실하게 예측하는 데 성공하지 못하며, 종종 노이즈가 많고 충실도가 낮은 기하학 근사치를 생성한다.

우리는 VolSDF가 신경 볼륨 렌더링의 밀도에 대한 다른 모델을 고안하여 뷰 합성 품질을 유지하면서 장면의 지오메트리의 더 나은 근사치로 이어질 것을 제안한다.
핵심 아이디어는 밀도(density)를 장면 표면에 대한 부호 거리 함수로 표현하는 것입니다(그림 1 참조).
이러한 밀도 함수는 여러 가지 이점을 누린다.
첫째, 밀도를 생성하는 잘 정의된 표면의 존재를 보장한다.
이는 밀도 및 광도 필드를 분리하는 데 유용한 유도 바이어스를 제공하여 보다 정확한 지오메트리 근사치를 제공한다.
둘째, 우리는 이 밀도 제형이 광선을 따라 불투명도의 근사 오차를 제한할 수 있다는 것을 보여준다.
이 경계는 뷰레이를 샘플링하여 볼륨 렌더링 적분의 밀도 및 광도 필드의 충실한 결합을 제공하는 데 사용됩니다.
예를 들어, 그러한 경계가 없다면, 광선(픽셀 색상)을 따라 계산된 광도는 잠재적으로 표면 부분을 놓치거나 확장하여 잘못된 광도 근사로 이어질 수 있다.
흔히 신경 암묵적 표면 [26, 43, 15]이라고 하는 밀접하게 관련된 연구 라인은 신경망을 사용하여 암시적으로 장면의 형상을 표현하는 데 초점을 맞춰 표면 렌더링 프로세스를 차별화했다.
이러한 방법의 가장 큰 단점은 배경에서 물체를 분리하는 마스크가 필요하다는 것이다.
또한 표면을 직접 렌더링하는 방법을 배우면 볼륨 렌더링으로 인해 최적화 문제로 인해 관련 없는 부분이 커지는 경향이 있습니다.
어떤 의미에서, 우리의 작업은 두 세계의 장점을 결합합니다: 신경 암시 표면을 사용한 볼륨 렌더링.
DTU[13] 및 Blended-MVS[42] 데이터 세트에서 표면을 재구성하여 VolSDF의 유효성을 입증한다.
VolSDF는 NeRF[25] 및 NeRF++[45]에 비해 더 정확한 표면 재구성을 제공하며, IDR[43]과 비교해도 유사한 재구성을 수행하지만 개체 마스크 사용을 피한다.
또한, 우리는 NeRF 기반 모델에서 실패한 것으로 보이는 다른 장면의 밀도 및 광도 필드를 전환하는 방법, 즉 우리의 방법으로 분리 결과를 보여준다.
2. Related Work
신경 장면 표현&렌더링
암묵적 함수는 전통적으로 3D 장면 모델링에 채택된다[28, 12, 5].
최근 연구는 장면 표현[10, 24, 23, 27, 29, 34, 41, 32, 40]과 프리뷰 렌더링[38, 19, 35, 20, 25, 45, 39, 3]을 포함하여 표현력과 낮은 메모리 풋프린트로 인해 다층 퍼셉트론(MLP)을 사용한 모델 암묵적 함수에 초점을 맞추고 있다.
특히, NeRF [25]는 신경 암묵적 기능과 볼륨 렌더링을 결합하여 사실적인 렌더링 결과를 달성하는 연구 라인을 개설했다(개요는 [7] 참조).
그러나 예측된 밀도로부터 표면을 추출하기 위한 적절한 임계값을 찾는 것은 중요한 일이 아니며, 복구된 형상은 만족스럽지 못하다.
또한 픽셀 렌더링을 위한 광선을 따라 점의 샘플링은 정확한 근사치를 보장하지 않고 다른 네트워크에서 근사한 불투명도 함수를 사용하여 수행된다.
다중 뷰 3D 재구성
이미지 기반 3D 표면 재구성(멀티 뷰 스테레오)은 지난 수십 년 동안 오랫동안 문제가 되어 왔다.
기존의 다중 뷰 스테레오 접근 방식은 일반적으로 깊이 기반 [2, 36, 9, 8] 또는 복셀 기반 [6, 4, 37]입니다.
예를 들어, COLMAP [36](일반적인 깊이 기반 방법)에서 이미지 특징을 추출하고 다른 뷰에서 일치시켜 깊이를 추정한다.
그런 다음 예측된 깊이 맵을 융합하여 밀도 높은 포인트 클라우드를 얻는다.
표면을 얻기 위해 추가 메싱 단계(예: 포아송 표면 재구성이 적용된다[14].
그러나 복잡한 파이프라인이 있는 이러한 방법은 각 단계에서 오류가 누적될 수 있으며 특히 램버트가 아닌 표면은 뷰 의존적 색상을 처리할 수 없기 때문에 불완전한 3D 모델을 초래할 수 있다.
반대로 볼륨 내 객체를 직접 모델링해 완전한 모델을 제작하지만, 복셀 기반 접근 방식은 메모리 소모가 많아 저해상도로 한계가 있다.
최근에는 다중 뷰 이미지에서 장면 형상을 재구성하기 위해 DVR [26], IDR [43], NLR [15]와 같은 신경 기반 접근 방식도 제안되었다.
그러나 이러한 방법은 그레이디언트를 전파하기 어렵기 때문에 정확한 물체 마스크와 적절한 무게 초기화가 필요하다.
여기서의 연구와는 별개로 [31]은 볼륨 렌더링에 통합된 암묵적 표면 표현도 사용합니다.
특히 국소 투명 기능을 점유 네트워크로 대체한다[23].
이렇게 하면 손실에 지표면 평활 항을 추가하여 결과 지표면의 품질을 향상시킬 수 있습니다.
그들의 접근 방식과 달리, 우리는 명시적인 평활 용어 없이 에이코날 손실로 정규화된 부호 거리 표현을 사용한다[43, 11].
또한 부호 거리를 사용하면 불투명도 근사 오류를 제한할 수 있어 제안된 밀도 제품군에 필수적인 볼륨 렌더링의 근사치를 쉽게 만들 수 있음을 보여준다.
3. Method
이 절에서는 변환 부호 거리 함수로 정의된 볼륨 밀도에 대한 새로운 매개 변수화를 소개한다.
그런 다음 이 정의가 볼륨 렌더링 프로세스를 어떻게 촉진하는지 보여준다.
특히, 불투명도 근사치의 오차 한계를 도출하고 결과적으로 볼륨 렌더링 적분의 근사치를 위한 샘플링 절차를 고안한다.
3.1 Density as transformed SDF
집합 Ω ⊂ R^3이 R^3의 어떤 물체에 의해 점유된 공간을 나타내고 M= ∂Ω를 경계 표면에 나타내도록 한다.
우리는 1_Ω 지시 함수와 d_Ω으로 경계 M에 대한 부호 거리 함수(SDF)를 나타낸다,

, 여기서 ∥·∥는 표준 유클리드 2-노름이다.
부피 렌더링에서 부피 밀도 σ : R^3→R_+는 스칼라 부피 함수이며, 여기서 σ(x)는 점 x에서 빛이 가려지는 비율이다.
이전의 신경 체적 렌더링 접근법[25, 18, 45]에서, 밀도 함수 σ는 범용 다층 퍼셉트론 (MLP)으로 모델링되었습니다.
본 연구에서는 학습 가능한 부호 거리 함수(SDF) d_Ω의 특정 변환을 사용하여 밀도를 모델링할 것을 제안한다,

여기서 α, β > 0은 학습 가능한 매개변수이다, ψ_β는 평균과 β 척도가 0인 라플라스 분포의 누적 분포 함수(CDF)이다, (즉, 직관적으로 L_1 버전의 표준편차인 평균 절대편차),

그림 1(왼쪽 가운데와 오른쪽)은 이러한 밀도와 SDF의 예를 보여줍니다.
이 정의에서 쉽게 확인할 수 있듯이 β가 0에 가까워지면 밀도 σ는 Ω의 스케일링 지시 함수로 수렴된다, 즉, 모든 점 x ∈ Ω/M에 대해 σ → α1_Ω이다.
직관적으로, 밀도 σ는 일정한 밀도의 α를 가진 균일한 물체를 모델링하며, 여기서 평활량은 β에 의해 제어된다.
밀도를 식 (2)와 같이 정의하면 다음과 같은 두 가지 이점이 있다:
첫째, 표면 기하학 M에 유용한 유도 바이어스를 제공하고, d_Ω의 제로 레벨 집합으로 표면을 재구성하는 원칙적인 방법을 제공한다.
이는 재구성을 학습 밀도의 임의 수준 세트로 선택한 이전 연구와 대조적이다.
둘째, 식 (2)에서 정의한 밀도의 특정 형태는 볼륨 렌더링 파이프라인의 중요한 구성요소인 렌더링된 볼륨의 불투명도(또는 동등하게 투명도) 오류에 대한 경계를 용이하게 한다.
대조적으로, 그러한 바운드는 일반 MLP 밀도에 대해 고안하기 어려울 것이다.
3.2 Volume rendering of σ
이 섹션에서는 볼륨 렌더링 적분과 이를 근사화하는 데 일반적으로 사용되는 수치 적분을 검토하며, 레이당 샘플 포인트 세트 S가 필요하다.
다음 섹션(섹션 3.3)에서는 밀도 σ의 속성을 탐색하고 가시광선을 따라 불투명도 근사 오차에 대한 한계를 도출한다.
마지막으로 섹션 3.4에서는 볼륨 렌더링 수치 적분에 사용되는 샘플 S를 생성하기 위한 알고리즘을 도출한다.
볼륨 렌더링에서 우리는 x(t) = c + tv, t≥0으로 정의된 v ∈ R^3, |v| = 1 방향의 카메라 위치 c ∈ R^3에서 방출되는 선 x를 고려한다.
본질적으로, 볼륨 렌더링은 카메라에 도달하는 이 광선을 따라 통합된 (즉, 합산된) 빛의 광도를 근사화하는 것이다.
이 계산에 참여하는 두 가지 중요한 양이 있다: 부피의 불투명도 O 또는 동등하게, 전이성 T와 광도 필드 L.
T로 표시된 선 x에 따른 부피의 투명함수는 각 t≥0에 대해 광 입자가 튕기지 않고 세그먼트 [c, x(t)]을 통과할 확률을 나타낸다,

불투명도 O는 보합 확률이다,

O는 O(0) = 0인 단조증가함수이며, 모든 광선이 결국 O(∞) = 1이라고 가정한다.
그런 의미에서 우리는 O를 CDF라고 생각할 수 있다, 그리고

는 확률밀도함수(PDF)입니다.
볼륨 렌더링 식은 광선을 따라 예상되는 빛입니다,
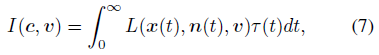
여기서 L(x, n, v)은 방사장, 즉 v 방향의 점 x에서 방출되는 빛의 양이다, 우리의 공식에서 우리는 L이 수준 집합의 정규에 의존하도록 허용한다, 즉, n(t) = ∇_xd_Ω(x(t))입니다.
이러한 의존성을 추가하는 것은 공통 재료의 BRDF가 표면 정상과 관련해 인코딩되는 경우가 많아 표면 렌더링에서와 같이 분리가 용이하다는 사실에 기인한다[43].
우리는 실험 부분에서 분리 문제로 다시 돌아가겠습니다.
식 (7)의 적분은 수치 직교법을 사용하여 근사한다, 직사각형 규칙이라 불리는, 즉, 일부 이산 표본 S={s_i}^m_i=1, 0=s_1<s_2<...<s_m=M에서, 여기서 M은 어떤 큰 상수이다:
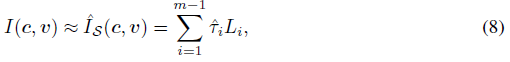
여기서 ^I_S의 첨자 S를 사용하여 근사치의 의존성을 강조합니다, 표본 집합 S, ^T_i ≒ T(s_i)△s는 근사 PDF에 구간 길이를 곱한 값입니다, L_i = L(x(s_i), n(s_i), v)은 샘플링된 광도 필드이다.
우리는 부록에 ^T_i의 완전한 파생과 세부 사항을 제공합니다.
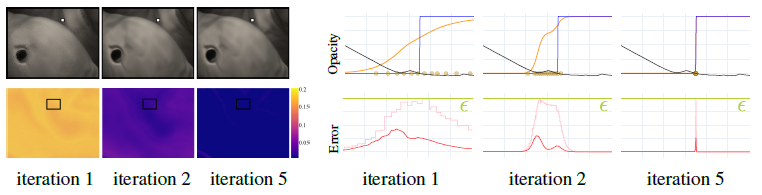
샘플링.
PDF T는 일반적으로 물체의 경계 근처에 극도로 집중되어 있기 때문에(예: 오른쪽 그림 3 참조) 표본점 S의 선택은 식 (8)의 근사 품질에 중요한 영향을 미친다.
한 가지 해결책은 예를 들어, 역 CDF로 계산된 S, 즉 O^-1과 같은 적응형 샘플을 사용하는 것이다.
그러나 O는 밀도 모델 σ에 의존하며 명시적으로 주어지지 않는다.
[25]의 두번째에서, 거친 네트워크는 불투명도 O의 근사치를 위해 특별히 훈련되었고 역 샘플링에 사용되었다.
그러나, 두 번째 네트워크의 밀도가 반드시 볼륨 적분을 계산하고자 하는 첫 번째 네트워크의 밀도를 충실하게 나타내는 것은 아닙니다.
또한, 우리가 나중에 보여주듯이, 한 단계의 샘플링은 정확한 샘플 S를 생산하기에 부족할 수 있습니다.
O의 순진하거나 조잡한 근사치를 사용하면 무시할 수 없는 T 값을 놓치거나 지나치게 확장하는 차선의 샘플 집합 S가 발생할 수 있습니다.
결과적으로 잘못된 광도 근사치(즉, 픽셀 색상)가 발생하여 학습된 밀도-방사장 분해를 잠재적으로 해칠 수 있다.
우리의 솔루션은 단일 밀도 σ로 작동하며, 샘플링 S는 불투명도 근사치에 대한 오차 한계를 기반으로 한 샘플링 알고리즘에 의해 계산된다.
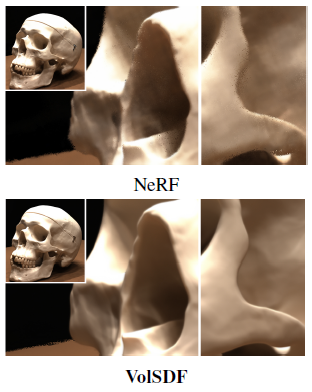
그림 2는 동일한 장면의 NeRF 및 VolSDF 렌더링을 비교합니다.
무작위 샘플로 인해 발생하는 NeRF 렌더링의 salt and pepper 아티팩트를 주목하십시오; NeRF에서 고정(균일된 간격) 샘플링을 사용하면 보충에 표시된 다른 유형의 아티팩트가 나타납니다.
3.3 Bound on the opacity approximation error
이 섹션에서는 직사각형 규칙을 사용하여 불투명도 근사 오류에 대한 경계를 개발한다.
검체 세트 T={t_i}^n_(i=1), 0=t_1<t_2<...<t_n=M의 경우, 우리는 δ_i=t_(i+1)-t_i, σ_i=σ(x(t_i))로 표기한다.
t∈(0,M]가 주어졌을 때, t∈[t_k, t_(k+1)]를 가정하고 직사각형 규칙(즉, 왼쪽 리만 합)을 적용하여 근사치를 구한다:
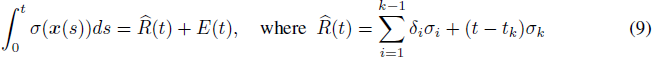
는 직사각형 규칙 근사치이며, E(t)는 이 근사치의 오류를 나타냅니다.
불투명도 함수(식 (5))의 해당 근사치는

입니다.
이 절에서 우리의 목표는 근사치 ^O≒O에 대한 [0, M]을 초과하는 균일한 경계를 도출하는 것이다.
핵심은 선 x(t)를 따라가는 구간 내 밀도 σ의 도함수에 대한 다음과 같은 경계이다.

정리 1의 장점은 구간의 끝점에서의 부호 없는 거리인 |d_i|, |d_(i+1)|와 밀도 매개변수 α, β 에 근거하여 [t_i, t_(i-1)]에서 밀도의 도함수를 묶을 수 있다는 것이다.
이 경계는 직사각형 규칙의 불투명도 근사치에 대한 오차 한계를 도출하는 데 사용될 수 있다.
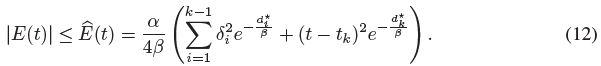
자세한 내용은 부록에 있습니다.
식 (12)는 다음과 같은 불투명도 오차 한계를 나타내며, 보충 자료에서도 증명되었다.
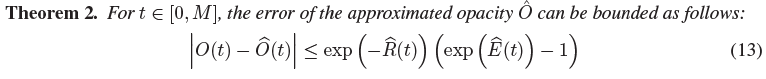
마지막으로, 우리는 ^E(t)와 exp(^E(t)가 t에서 단조롭게 증가하는 반면 exp(-^R(t)는 t에서 단조롭게 감소하는 것에 주목함으로써 t ∈ [t_k, t_(k+1)]에 대한 불투명도 오류를 제한할 수 있다, 그러므로,
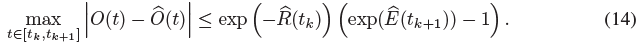
모든 간격에 걸쳐 최댓값을 취하면 T와 β의 함수로써 B_(T, β) 결합이 된다,
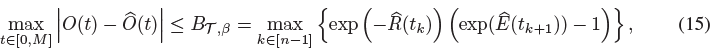
여기서 규칙 ^R(t_0) = 0, [l] = {1, 2, ..., l}.
그림 3을 참조하십시오, 여기서 이 경계는 희미한 빨간색으로 표시됩니다.
이 섹션을 마무리하기 위해 보충 자료에서 증명된 두 가지 유용한 속성을 도출한다.
첫째, 충분히 조밀한 샘플링은 오차 범위 B_(T, β)를 줄일 수 있다는 것을 보장한다:

3.4 Sampling Algorithm
이 섹션에서는 식 (8)에서 사용될 샘플링 S를 계산하는 알고리즘을 개발한다.
이것은 ^O (식 (10)을 통해)가 실제 불투명도 O에 대한 ε 근사치, 즉 ε는 초매개변수, 즉 B_(T, β)를 제공하기 위해 먼저 식 (15)의 경계를 사용하여 수행된다.
둘째, 섹션 3.2에 설명된 대로 ^O 를 사용하여 역 CDF 샘플링을 수행한다.
Lemma 1에서 B(T,β) < ε를 보장하기 위해 충분히 큰 n을 선택할 수 있다는 것을 주목하라.
하지만, 이것은 엄청나게 많은 수의 샘플로 이어질 것입니다.
대신, 우리는 실제로 필요한 샘플의 수를 줄이고 제한된 샘플 포인트의 예산으로 작업할 수 있는 간단한 알고리즘을 제안한다.
간단히 말해서, 우리는 균일한 샘플링 T = T_0으로 시작하고, Lemma 2를 사용하여 처음에 B_(T, β_+)≤ε을 만족시키는 β_+ > β를 설정한다.
그런 다음 B_(T, β_+) ≤ ε를 유지하면서 β+를 줄이기 위해 T 표본을 반복적으로 상향 추출한다.
이 간단한 전략은 수렴이 보장되지 않지만, 우리는 β_+가 일반적으로 β로 수렴된다는 것을 발견한다(일반적으로 85% 그림 3 참조), 그렇지 않은 경우에도 알고리즘은 불투명도 근사가 여전히 ε 오류를 유지하는 β_+를 제공한다.
알고리즘은 아래에 제시되어 있습니다(알고리즘 1).
3.5. Training
4. Experiments
우리는 멀티뷰 3D 표면 재구성이라는 어려운 과제에 대한 우리의 방법을 평가한다.
두 가지 데이터 세트를 사용합니다: DTU [13] 및 BlendedMVS [42], 둘 다 다중 뷰에서 캡처한 서로 다른 재료를 가진 실제 개체를 포함합니다.
섹션 4.1에서는 관련 기준선과 비교하여 VolSDF의 질적 및 정량적 3D 표면 재구성 결과를 보여준다.
섹션 4.2에서 우리는 NeRF[25]와 대조적으로 모델이 캡처된 물체의 형상과 외관을 성공적으로 분리할 수 있음을 보여준다.
4.1 Multi-view 3D reconstruction
DTU
DTU [13] 데이터 세트에는 고정 카메라 및 조명 파라미터로 다양한 개체의 다중 뷰 이미지(49 또는 64)가 포함되어 있습니다.
우리는 [43]에 의해 선택된 15개의 스캔에 대해 우리의 방법을 평가한다.
Chamfer l_1 loss(mm 단위로 측정)을 사용하여 표면 정확도를 COLMAP_0(수밀 재구성)과 비교한다; COLMAP_7은 물이 새지 않으며 참고용으로만 제공됨) [36], NeRF [25] 및 IDR [43], 여기서 IDR과의 공정한 비교를 위해 개체의 시각적 선체 내부 재구성만 평가한다([43]의 분할 마스크에 의해 정의됨).
[25]와 비교하여 렌더링의 PSNR을 추가로 평가한다.
정량적 결과는 표 1에 제시되어 있다.
우리의 방법이 (모든 이미지에 객체 마스크를 사용하는) IDR과 동등하고 재구성 정확도 측면에서 NeRF 및 COLMAP보다 우수하다는 것을 관찰할 수 있다.
우리의 렌더링 품질은 NeRF와 비슷합니다.
BlendedMVS
BlendedMVS 데이터 세트 [42]에는 다중 뷰에서 캡처한 113개 장면의 대규모 모음이 포함되어 있다.
평가를 위한 고품질 ground truth 3D 모델, 다양한 카메라 구성, 다양한 실내/외 실제 환경을 제공합니다.
우리는 9개의 다른 장면을 선택하고 우리의 방법을 사용하여 각 물체의 표면을 재구성했습니다.
DTU 데이터셋과 달리 BlendedMVS 장면은 복잡한 배경을 가지고 있습니다.
따라서 이 데이터 세트의 기준으로 NeRF++[45]를 사용합니다.
표 2에서는 NeRF++와 비교한 결과를 제시한다.
질적 비교는 그림 5에 제시되어 있다; 이 경우 단위를 알 수 없기 때문에 NeRF에 비해 Chamfer 거리(%)의 상대적 개선을 제시한다.
또한 이 경우 렌더링 품질(PSNR) 측면에서 동등하면서 NeRF 재구성을 상당히 개선한다.
[43]과의 비교
IDR [43]은 암묵적 표현을 사용한 최첨단 3D 표면 재구성 방법이다.
그러나 다음과 같은 두 가지 단점이 있다:
첫째, 그것은 훈련을 위한 강력한 감독 신호인 물체 마스크를 요구합니다.
둘째, 해당 가시광선의 단일 교차점만을 기준으로 픽셀 색상을 설정하기 때문에 때로는 외부 표면 부분의 형태로 나타나는 국소 최소점으로 더 잘 정리된다.
그림 6은 IDR로 훈련한 동일한 장면과 지상 진리 마스크를 추가한 장면을 비교하고, 마스크 없이 훈련한 VolSDF를 비교한다.
IDR은 일부 관련 없는 표면 부분(예: 빨간색으로 표시된 부분)을 사용하는 반면, VolSDF는 이 경우에 더 충실한 결과를 제공합니다.
4.2 Disentanglement of geometry and appearance
우리는 훈련된 두 장면의 광도 필드를 전환하여 장면의 기하학적 구조(밀도)와 외관(발광 영역)으로의 분리를 테스트했다.
VolSDF의 경우 L_ψ로 전환했습니다.
NeRF [25]의 경우, 우리는 방사장이 L_ψ(z, v)로 계산된다는 것을 주목한다, 여기서 L_ψ은 하나의 은닉 레이어(너비 128 및 ReLU 활성화)가 있는 완전히 연결된 네트워크이고 z는 형상 벡터이다.
두 가지 버전의 NeRF 분리를 테스트했습니다.
첫째, 훈련된 NeRF 네트워크의 원래 광도 필드 L_ψ을 전환함으로써.
둘째, 동일한 광도 필드 모델을 가진 훈련된 NeRF 모델의 광도 필드를 우리의 것으로 전환함으로써, 즉 L_ψ(x, n, v, z)한다.
그림 7에서 볼 수 있듯이, 두 버전의 NeRF는 이러한 장면에서 정확한 분리를 생성하지 못하는 반면, VolSDF는 성공적으로 두 물체의 재료를 전환한다.
우리는 이것을 방정식 2의 밀도를 사용하여 주입된 특정 유도 편향 때문이라고 본다.
5. Conclusions
암묵적 신경 표면을 위한 볼륨 렌더링 프레임워크인 VolSDF를 소개한다.
우리는 부피 밀도를 학습된 표면 형상에 대한 서명 거리 함수의 변환된 버전으로 나타낸다.
단순해 보이는 이 정의는 유용한 귀납적 바이어스를 제공하여 기하학(즉, 밀도)과 광도장을 분리할 수 있고 이전의 신경 체적 렌더링 기술에 비해 기하학 근사치를 향상시킨다.
또한 불투명도 근사 오류를 제한하여 볼륨 렌더링 적분의 높은 충실도 샘플링을 수행할 수 있습니다.
우리 방법의 몇 가지 한계는 흥미로운 미래 연구 기회를 제시한다.
첫째, 실제로는 잘 작동하지만 샘플링 알고리즘에 대한 정확성 증거가 없다.
우리는 그러한 증거를 제공하거나 증거가 있는 이 알고리즘의 버전을 찾는 것이 유용할 것이라고 믿는다.
일반적으로 볼륨 렌더링의 한계를 가지고 작업하면 학습과 분리를 개선하고 필드를 발전시킬 수 있다고 믿는다.
둘째, 제로 두께 표면과 같은 경계로 비수밀 매니폴드 및/또는 매니폴드를 나타내는 것은 SDF로 불가능하다.
여러 함축적 의미와 서명되지 않은 필드와 같은 일반화는 가치가 있다는 것을 증명할 수 있다.
셋째, 현재 공식은 균질 밀도를 가정한다. 이를 보다 일반적인 밀도 모델로 확장하면 더 넓은 종류의 형상을 나타낼 수 있다.
넷째, 고품질 기하학을 비지도 방식으로 학습할 수 있으므로 동적 기하학을 배우고 이미지 컬렉션에서 직접 공간을 형상화하는 것이 흥미로울 것이다.
마지막으로, 우리의 작업이 즉각적인 부정적인 사회적 영향을 미치지는 않지만, 이미지로부터의 정확한 지오메트리 재구성은 악의적 목적으로 사용될 수 있다는 점에 주목한다.