2022. 3. 4. 11:48ㆍ3D Vision
Pixel2Mesh : Generating 3D Mesh Models from Single RGB Images
Nanyang Wang, Yinda Zhang, Zhuwen Li, Yanwei Fu, Wei Liu, Yu-Gang Jiang
Abstract
단일 컬러 이미지에서 삼각형 메시로 3D 형상을 생성하는 엔드 투 엔드 딥 러닝 아키텍처를 제안한다.
심층 신경망의 특성으로 인해 제한되는 이전 방법은 대개 볼륨 또는 포인트 클라우드에서 3D 형상을 나타내며, 이를 즉시 사용할 수 있는 메시 모델로 변환하는 것이 중요하다.
기존 방법과 달리, 우리 네트워크는 그래프 기반 컨볼루션 신경망에서 3D 메시를 나타내며 입력 이미지에서 추출된 지각 특징을 활용하여 타원체를 점진적으로 변형하여 올바른 형상을 만든다.
우리는 전체 변형 절차를 안정적으로 만들기 위해 coarse-to-fine 전략을 채택하고, 시각적으로 매력적이고 물리적으로 정확한 3D 형상을 보장하기 위해 다양한 수준의 속성을 캡처하기 위해 다양한 메시 관련 손실을 정의한다.
광범위한 실험에 따르면 우리의 방법은 더 나은 디테일을 가진 메시 모델을 질적으로 생산할 뿐만 아니라 최첨단 기술에 비해 더 높은 3D 형상 추정 정확도를 달성한다.
1. Introduction
단일 관점에서 3D 모양을 유추하는 것은 인간의 기본적인 비전 기능이지만 컴퓨터 비전에는 매우 어렵다.
최근에는 딥러닝 기술을 사용하여 단일 컬러 이미지에서 3D 형상을 생성하는 데 큰 성공을 거두었다[6, 9].
일반 그리드 또는 다층 인식의 컨볼루션 레이어를 활용하여 신경망의 출력으로서 추정된 3D 형상은 볼륨 [6] 또는 포인트 클라우드 [9]로 표현된다.
그러나 두 표현 모두 중요한 표면 세부 정보를 잃고 표면 모델(그림 1)을 재구성하는 것이 중요하지 않다, 즉, 메시는 가볍고 모양 세부 정보를 모델링할 수 있으며 애니메이션에 변형하기 쉽기 때문에 많은 실제 애플리케이션에 더 바람직하다.

본 논문에서는 단일 이미지 재구성 방향을 추진하고, 단일 컬러 이미지에서 3D 삼각형 메시를 추출하는 알고리즘을 제안한다.
우리 모델은 직접 합성하는 대신 메쉬를 평균 모양에서 대상 지오메트리로 변형하는 방법을 배운다.
이것은 우리에게 몇 가지 측면에서 이득이 됩니다.
첫째, 심층 네트워크는 그래프와 같은 구조화된 출력보다 공간 변형과 같은 잔류물을 예측하는 데 더 좋다.
두 번째, 일련의 변형들이 함께 더해질 수 있기 때문에 모양을 점진적으로 세밀하게 다듬을 수 있습니다.
또한 딥러닝 모델의 복잡성과 결과의 품질 사이의 절충을 제어할 수 있다.
마지막으로, 초기 메쉬(예: 위상)에 대한 사전 지식을 인코딩할 수 있는 기회를 제공한다.
선구적인 연구로서, 본 연구에서는 고정된 크기의 타원체를 변형하여 속이 0인 3D 메시를 사용하여 근사할 수 있는 물체에 대해 구체적으로 연구한다.
실제로 일반적으로 볼 수 있는 대부분의 범주는 자동차, 비행기, 테이블 등과 같은 이 설정 하에서 잘 처리될 수 있다는 것을 발견했다.
이 목표를 달성하기 위해서는 몇 가지 난제가 내재되어 있다.
첫 번째 과제는 본질적으로 불규칙 그래프인 메시 모델을 신경망에서 나타내면서도 2D 정규 그리드로 표현된 주어진 색상 이미지에서 형상 세부 정보를 효과적으로 추출할 수 있는 방법이다.
두 가지 데이터 양식에서 학습한 지식의 통합이 필요하다.
3D 기하학 측면에서 메시의 정점과 가장자리가 그래프의 노드와 연결로 직접 표현되는 메시 모델에 그래프 기반 fully convolutional network (GCN)[3, 8, 18]을 구축한다.
3D 쉐이프에 대한 네트워크 피쳐 인코딩 정보가 각 정점에 저장됩니다.
정방향 전파를 통해 컨볼루션 레이어는 인접한 노드 간에 특징 교환을 가능하게 하고, 결국 각 정점에 대한 3D 위치를 회귀시킨다.
2D 이미지 측면에서, 우리는 VGG-16과 유사한 아키텍처를 사용하여 많은 작업에서 성공적인 것으로 입증되었으므로 특징을 추출한다[10, 20].
이 두 가지를 연결하기 위해 GCN의 각 노드가 이미지의 2D 투영에서 이미지 특징을 풀링할 수 있는 지각 피처 풀링 레이어를 설계한다. 이는 알려진 카메라 고유 매트릭스를 가정하여 쉽게 얻을 수 있다.
지각 특징 풀링은 업데이트된 3D 위치를 사용하여 몇 가지 컨볼루션(섹션 3.4에서 설명한 변형 블록) 후에 한 번 활성화되며, 따라서 정확한 위치의 이미지 특징을 3D 모양과 효과적으로 통합할 수 있다.
그래프 표현을 고려할 때, 다음 과제는 정점 위치를 ground-truth로 효과적으로 업데이트하는 방법이다.
실제로 정점 수가 많은 메시를 직접 예측하도록 훈련된 네트워크는 초기에 실수하고 나중에 수정하기 어렵다는 것을 관찰한다.
한 가지 이유는 정점이 제한된 수용 필드, 즉 가장자리 수가 멀리 있는 다른 정점에서 형상을 효과적으로 검색할 수 없기 때문이다.
이 문제를 해결하기 위해, 우리는 네트워크가 더 적은 정점으로 시작하고 전진 전파 중에 증가할 수 있는 그래프 압축 해제 계층을 설계한다.
시작 단계에서 정점이 더 적으면 네트워크는 정점을 가장 대표적인 위치로 분배한 다음 나중에 정점의 수가 증가함에 따라 로컬 세부 정보를 추가하는 방법을 학습한다.
그래프 언쿨링 레이어 외에도, 우리는 아키텍처의 중추로 바로 가기 연결[13]에 의해 강화된 심층 GCN을 사용하여 글로벌 컨텍스트와 더 많은 이동 단계를 위한 대규모 수용 필드를 가능하게 한다.
도형을 그래프로 표현하는 것도 학습 과정에 도움이 된다.
알려진 연결을 통해 인접 노드 간에 고차 손실 함수를 정의할 수 있으며, 이는 3D 형상을 정규화하는 데 중요하다.
구체적으로, 우리는 매끄러운 표면을 선호하기 위해 표면 정상 손실, 높은 리콜을 위해 메시 정점의 균일한 분포를 장려하기 위한 에지 손실, 메시 면이 서로 교차하는 것을 방지하기 위한 라플라시안 손실을 정의한다.
이러한 모든 손실은 품질 좋은 메시 모델을 생성하는 데 필수적이며, 그래프 표현 없이는 그 어떤 것도 3차적으로 정의할 수 없다.
이 논문의 기여는 주로 세 가지 측면에 있다.
먼저, 우리는 단일 RGB 이미지에서 3D 메시 모델을 생성하는 새로운 종단 간 신경망 아키텍처를 제안한다.
둘째, 우리는 지각 이미지 특징을 GCN으로 표현되는 3D 지오메트리에 통합하는 투영 레이어를 설계한다.
셋째, 우리 네트워크는 3D 기하학을 coarse-to-fine하게 예측하여 더 신뢰할 수 있고 배우기 쉽다.
2. Related Work
문헌에서 multi-view geometry(MVG)[12]를 기반으로 3D 재구성이 잘 연구되었다.
주요 연구 방향에는 대규모 고품질 재구성을 위한 structure from motion(SfM)[27]와 내비게이션을 위한 simultaneous localization and mapping(SLAM)[4]이 포함된다.
이러한 시나리오에서는 매우 성공적이지만 1) 다중 뷰가 제공할 수 있는 범위와 2) 재구성하려는 객체의 모양에 의해 제한됩니다.
전자의 제한은 MVG가 객체의 보이지 않는 부분을 재구성할 수 없으므로 일반적으로 좋은 재구성을 위해 충분한 뷰를 얻는 데 오랜 시간이 소요된다는 것을 의미한다; 후자의 제한은 MVG가 비-람버트적(예: 반사 또는 투명) 또는 질감이 없는 객체를 재구성할 수 없다는 것을 의미한다.
이러한 제한은 학습 기반 접근법에 의존하는 추세로 이어진다.
학습 기반 접근법은 데이터로부터 배울 수 있는 모양에 크게 의존하기 때문에 일반적으로 단일 또는 소수의 이미지를 고려한다.
초기 연구는 Hoiem et al.[14]과 Saxena et al.[25]까지 거슬러 올라갈 수 있다.
가장 최근에는 딥러닝 아키텍처의 성공과 ShapeNet[5]과 같은 대규모 3D 형상 데이터 세트가 출시되면서 학습 기반 접근법이 큰 진전을 이루었다.
Huang et al.[15]와 Su et al.[29] 대형 데이터 세트에서 형상 구성 요소를 검색하여 조립하고 관찰된 이미지에 맞게 조립된 형상을 변형합니다.
그러나 이미지로부터의 형상 검색은 그 자체로 좋지 않은 문제이다.
이 문제를 피하기 위해, Kar et al.[16]은(는) 각 객체 범주에 대한 3D 변형 모델을 학습하고 다른 이미지의 형상 변화를 캡처합니다.
그러나 재구성은 인기 있는 범주로 제한되고 재구성 결과는 대개 세부 사항이 부족하다.
또 다른 연구 분야는 단일 이미지에서 3D 모양을 직접 학습하는 것입니다.
널리 보급된 그리드 기반 딥러닝 아키텍처에 의해 제한되는 대부분의 작업[6, 11]은 최신 GPU의 메모리 제약으로 인해 대개 낮은 해상도를 갖는 3D 복셀을 출력한다.
가장 최근에 Tatarchenko et al.[30]은 제한된 메모리 예산으로 고해상도 출력을 재구성할 수 있는 옥트리 표현을 제안했다.
그러나 3D 복셀은 여전히 게임과 영화 산업에서 인기 있는 형태 표현은 아니다.
복셀 표현의 단점을 피하기 위해, Fan et al.[9] 단일 이미지에서 포인트 클라우드 생성을 제안합니다.
포인트 클라우드 표현은 포인트 사이에 로컬 연결이 없으므로 포인트 위치의 자유도가 매우 크다.
따라서 생성된 포인트 클라우드는 일반적으로 지표면에 가깝지 않으며 3D 메시를 직접 복구하는 데 사용할 수 없다.
이러한 일반적인 3D 표현 외에도, 3D 형태를 나타내기 위해 소위 "기하학 영상"을 사용하는 흥미로운 연구[28]가 있다.
따라서, 그들의 네트워크는 이미지 대 이미지 매핑을 수행하는 2D 컨볼루션 신경망이다.
우리의 연구는 대부분 두 개의 최근 연구[17]와 [24]와 관련이 있다.
그러나 전자는 단순한 실루엣 감독을 채택하기 때문에 자동차, 램프 등과 같은 복잡한 물체에 대해서는 잘 수행되지 않는다; 후자는 결합 모델을 생성하기 위해 큰 모델 저장소가 필요하다.
우리의 기본 네트워크는 그래프 신경망[26]이며, 이 아키텍처는 형상 분석에 채택되었다[31].
한편, 형상 분석을 위해 표면 매니폴드에 컨볼루션을 직접 적용하는 차트 기반 방법도 있다[2, 22, 23].
우리가 아는 한, 그래프와 표면 매니폴드는 메쉬된 객체에 대한 자연스러운 표현이지만, 이러한 아키텍처는 단일 이미지에서 3D 재구성을 위해 채택된 적이 없다.
그래프 신경망, 차트 작성 기반 방법 및 그 적용에 대한 포괄적인 이해는 이 설문 조사 [3]를 참조하십시오.
3. Method
3.1 Preliminary: Graph-based Convolution
먼저 그래프 기반 컨볼루션에 대한 몇 가지 배경을 제공한다; 자세한 소개는 [3]에서 확인할 수 있다.
3D 메시는 3D 객체의 모양을 정의하는 정점, 모서리 및 면의 모음입니다; 그래프 M= (V, E,F), 여기서 V = {v_i}^N _i=1은 메쉬에서 N개의 꼭짓점 집합이고, E = {e_i}^E _i=1은 각 꼭짓점을 연결하는 E 모서리의 집합이며, F = {f_i}^N _i=1은 꼭짓점에 부착된 형상 벡터이다.
그래프 기반 컨볼루션 레이어는 불규칙 그래프에서 다음과 같이 정의된다:
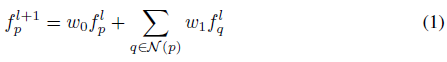
여기서 f^l _p ∈ R^(d_l), f^(l+1) _p ∈ R^(d_(l+1))은 컨볼루션 전후의 꼭지점 p에 대한 특징 벡터이고, N(p)은 p의 인접 꼭지점입니다; w_0과 w_1은 모두 적용되는 d_l × d_(l+1)의 학습 가능한 매개변수 행렬입니다.
w_1은 모든 에지에 대해 공유되므로, (1)은 다른 꼭짓점 각도를 가진 노드에서 작동한다.
이 경우, 부착된 형상 벡터 f_p는 3D 정점 좌표, 형상 인코딩 3D 형상 및 입력 색상 이미지(있는 경우)에서 학습한 형상들의 결합이다.
컨볼루션을 실행하면 변형을 적용하는 것과 동일한 기능이 업데이트됩니다.

우리 모델은 단일 컬러 이미지를 입력으로 사용하고 카메라 좌표에서 3D 메시 모델을 생성하는 엔드 투 엔드 딥러닝 프레임워크이다.
우리 프레임워크의 개요는 그림 2에 설명되어 있다.
전체 네트워크는 이미지 피쳐 네트워크와 계단식 메시 변형 네트워크로 구성된다.
이미지 피쳐 네트워크는 입력 이미지에서 perceptual feature를 추출하는 2D CNN으로, 메시 변형 네트워크가 타원체 메시를 원하는 3D 모델로 점진적으로 변형하기 위해 활용한다.
계단식 메시 변형 네트워크는 그래프 기반 컨볼루션 네트워크(GCN)로, 두 개의 그래프 압축 해제 레이어가 교차하는 세 개의 변형 블록을 포함한다.
각 변형 블록은 정점에 3D 형상 피쳐가 부착된 현재 메시 모델을 나타내는 입력 그래프를 취하고 새로운 정점 위치와 형상을 생성한다.
그래프 압축 해제 레이어는 정점의 수를 증가시켜 세부 정보 처리 용량을 증가시키는 반면 삼각형 메시 위상은 유지한다.
적은 수의 정점에서 시작하여, 우리의 모델은 coarse-to-fine 메쉬 모델에 세부 사항을 점진적으로 변형하고 추가하는 방법을 배운다.
네트워크가 안정적인 변형을 생성하고 정확한 메시를 생성하도록 학습하기 위해, 우리는 Fan et al.[9]이 사용하는 챔퍼 거리 손실을 표면 정규화 손실, 라플라시안 정규화 손실 및 에지 길이 손실이라는 세 가지 메시 특이적 손실과 함께 확장한다.
이 섹션의 나머지 부분에서는 이러한 구성 요소의 세부 정보를 설명합니다.
3.3 Initial ellipsoid
우리의 모델은 3D 형상에 대한 사전 지식이 필요하지 않으며, 항상 카메라 좌표의 공통 위치에 배치된 평균 크기의 초기 타원체에서 변형된다.
타원체는 카메라 앞 0.8m에 3축의 반지름으로 0.2m, 0.2m, 0.4m의 중심에 있습니다.
메쉬 모델은 Mashlab [7]의 암묵적 표면 알고리즘에 의해 생성되며 156개의 정점을 포함한다.
우리는 이 타원체를 사용하여 입력 그래프를 초기화하는데, 여기서 초기 기능은 각 정점의 3D 좌표만 포함한다.

3.4 Mesh deformation block
메시 변형 블록의 구조는 그림 3 (a)에 나와 있습니다.
입력 이미지에 표시된 객체와 일치하는 3D 메시 모델을 생성하려면 변형 블록이 입력 이미지에서 피쳐(P)를 풀링해야 합니다.
이 작업은 현재 메시 모델에서 정점 위치(C_(i-1))가 주어진 이미지 피쳐 네트워크 및 perceptual feature 풀링 레이어와 함께 수행된다.
그런 다음, 풀링된 perceptual feature은 입력 그래프(F_(i-1))의 정점에 부착된 3D 형상 특징과 연결되고 일련의 그래프 기반 ResNet(G-ResNet)에 공급된다.
G-ResNet은 메쉬 변형 블록의 출력물로서 다음을 생성한다, 각 꼭짓점에 대한 새 좌표(C_i) 및 3D 형상 피쳐(F_i)에 대한 값을 구한다.
Perceptual feature pooling layer
VGG-16 아키텍처를 널리 쓰이고 있는 것처럼 레이어 conv5_3까지 이미지 피쳐 네트워크로 사용합니다.
정점의 3D 좌표가 주어지면 카메라 본질을 사용하여 입력 이미지 평면에서 2D projection을 계산한 다음 bilinear interpolation을 사용하여 근처 4개의 픽셀에서 피쳐를 풀링한다.
특히, 우리는 레이어 'conv3_3', 'conv4_3' 및 'conv5_3'에서 추출한 피쳐를 연결하여 총 차원이 1280이 된다.
그런 다음 이 perceptual feature은 입력 메시의 128차원 3D 형상과 결합되어 총 차원이 1408이 된다.
이는 그림 3 (b)에 설명되어 있다.
첫 번째 블록에서 perceptual feature은 처음에 학습된 형상 feature가 없기 때문에 3차원 형상(좌표)과 연관된다.
G-ResNet
3D 모양과 2D 이미지 정보를 모두 나타내는 각 정점에 대해 1408차원 형상을 얻은 후, 각 정점에 대한 새로운 위치와 3D 형상 피쳐를 예측하는 그래프 기반 컨볼루션 신경망을 설계한다.
이를 위해서는 정점 간의 효율적인 정보 교환이 필요하다.
그러나 (1)에서 정의한 바와 같이, 각 컨볼루션은 인접한 픽셀 간의 피쳐 교환만 가능하게 하여 정보 교환의 효율성을 심각하게 손상시킨다.
이것은 2D CNN의 소규모 수용 현장 이슈와 같습니다.
이 문제를 해결하기 위해 바로 가기 연결 [13]로 매우 깊은 네트워크를 만들고 G-ResNet으로 표시합니다(그림 3 (a)).
본 연구에서, 모든 블록의 G-ResNet은 128개의 채널이 있는 14개의 그래프 잔여 컨볼루션 레이어로 구성된 동일한 구조를 가지고 있다.
G-ResNet 블록의 일련은 새로운 128차원 3D 피쳐를 생산한다.
피쳐 출력 외에도, 추가 그래프 컨볼루션 레이어를 마지막 도면층 형상에 적용하고 정점의 3D 좌표를 출력하는 브랜치가 있다.
3.5 Graph unpooling layer
unpooling layer의 목적은 GCNN의 정점 수를 증가시키는 것이다.
정점이 적은 메시에서 시작해 필요할 때만 추가할 수 있어 메모리 비용을 절감하고 더 나은 결과를 얻을 수 있다.
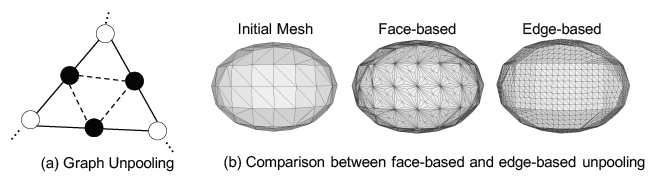
간단한 접근법은 각 삼각형의 중심에 하나의 꼭지점을 추가하고 삼각형의 세 꼭지점과 연결하는 것이다(그림 4 (b) 면 기반).
그러나 이것은 불균형 정점 각도, 즉 정점의 가장자리 수를 유발한다.
컴퓨터 그래픽에 널리 퍼져 있는 메쉬 세분화 알고리즘의 정점 추가 전략에서 영감을 받아 각 에지의 중앙에 정점을 추가하고 이 에지의 두 끝점과 연결한다(그림 4 (a))
새로 추가된 정점에 대한 3D 형상은 두 이웃의 평균으로 설정됩니다.
또한 세 꼭짓점이 동일한 삼각형(점선)에 추가되는 경우 연결한다.
결과적으로, 우리는 원래 메쉬의 각 삼각형에 대해 4개의 새로운 삼각형을 만들고, 정점의 수는 원래 메쉬의 가장자리 수만큼 증가한다.
이 에지 기반 압축 해제는 그림 4 (b) 에지 기반에 표시된 것처럼 정점을 균일하게 상향 조정한다.
3.6 Losses
우리는 출력 형상의 속성을 제한하기 위한 네 가지 종류의 손실과 호소력 있는 결과를 보장하기 위한 변형 절차를 정의한다.
메시 정점의 위치를 제한하기 위해 Chamfer loss[9]을 채택하고, 표면 정규성의 일관성을 강화하기 위한 normal loss, 변형 중에 인접 정점 사이의 상대적 위치를 유지하기 위한 laplacian regularization, 특이치를 방지하기 위한 edge length regularization를 채택한다.
이러한 손실은 중간 메시와 최종 메시 모두에 동일한 가중치로 적용됩니다.
달리 명시되지 않는 한, 우리는 예측 메시의 정점에 p를 사용하고, ground-truth 메시의 정점에 q를 사용하고, p의 이웃 픽셀에 대해 N(p)을 이 섹션의 끝까지 사용한다.
Chamfer loss
Chamfer 거리는 각 점과 다른 세트의 거리를 측정합니다:
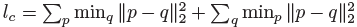
정점을 올바른 위치에 가깝게 회귀시키는 것은 상당히 좋지만, 좋은 3D 메시를 만들어내기에는 충분하지 않습니다 (그림 1의 Fan et al. [9]의 결과 참조).
Normal loss
우리는 고차 특성을 특징짓기 위해 표면 정규에서의 손실을 추가로 정의한다:

여기서 q는 Chamfer loss를 계산할 때 발견되는 p의 가장 가까운 꼭짓점이고, k는 p의 이웃 픽셀이며, <·, ·>는 두 벡터의 내부 곱이고, n_q는 ground truth에서 정규로 관측된 표면이다.
본질적으로, 이 손실은 ground truth로부터의 관측에 수직인 이웃을 가진 꼭짓점 사이의 가장자리를 필요로 한다.
평면이 아니라면 이 손실이 0이 아니라는 것을 알 수 있다.
그러나 이 손실을 최적화하는 것은 지역 적합 접선 평면의 정규성이 실험에서 실질적으로 잘 작동하는 관측치와 일치하도록 하는 것과 같다.
더욱이, 이 정상적인 손실은 완전히 차별화 될 수 있고 최적화하기 쉽습니다.

Regularization
Chamfer 손실과 일반 손실에도 불구하고 최적화는 일부 로컬 최소값에 쉽게 고착됩니다.
보다 구체적으로, 네트워크는 일부 로컬 일관성을 선호하기 위해 일부 초대형 변형을 생성할 수 있으며, 이는 특히 추정이 실제와 동떨어져 있을 때 초기에 해롭고 정점 비행을 유발한다(그림 5).
Laplacian regularization
이러한 문제를 처리하기 위해, 우리는 먼저 메쉬 자체 교차를 잠재적으로 피할 수 있는 정점이 너무 자유롭게 움직이는 것을 방지하기 위해 라플라시안 항을 제안한다.
라플라이안 항은 인접한 정점이 동일한 움직임을 갖도록 장려하는 로컬 상세 보존 연산자 역할을 합니다.
첫 번째 변형 블록에서, 이 블록에 대한 입력은 타원체가 매우 평활하기 때문에 표면 평활도 항처럼 작용한다; 두 번째 블록부터는 3D 메쉬 모델이 너무 변형되는 것을 방지하여 세밀한 디테일만 메쉬 모델에 추가할 수 있습니다.
이 손실을 계산하기 위해, 우리는 먼저 각 꼭짓점 p에 대한 라플라시안 좌표를
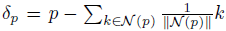
로 정의하고, 라플라시안 정규화를 다음과 같이 정의한다: l_lap=∑_p||δ'_p - δ_p||^2_2, 여기서 δ_p와 δ_p는 변형 블록 앞과 뒤의 꼭지점의 라플라시안 좌표이다.
Edge length regularization
일반적으로 긴 모서리를 유발하는 비행 정점을 벌하기 위해 가장자리 길이 정규화 손실을 추가한다:

전체 손실은 4개의 손실인 l_all=l_c+λ_1·l_n+λ_2·l_lap+λ_3·l_loc의 가중치 합으로, 여기서 λ_1=1.6e-4, λ_2=0.3 및 λ_3=0.1은 손실의 균형을 맞추고 모든 실험에 대해 고정된 초모수입니다.
4. Experiment
5. Conclusion
단일 이미지에서 3D 삼각 메시를 추출하는 방법을 제시하였다.
우리는 메시 프레젠테이션이 우리에게 가져올 수 있는 주요 장점과 성공을 위해 해결해야 하는 주요 문제를 활용한다.
전자는 표면 정상 제약과 가장자리를 따른 정보 전파를 포함하며, 후자는 이미지에서 추출한 지각 특징을 지침으로 포함한다.
우리는 네트워크 구조를 신중하게 설계하고 "지름길" 연결이 있는 매우 깊은 계단식 그래프 컨볼루션 신경망을 제안한다.
메시는 Chamfer loss와 normal loss로 종단 간 훈련된 네트워크에 의해 점진적으로 개선된다.
우리의 결과는 3D 볼륨 또는 3D 포인트 클라우드와 같은 다른 형상 표현을 사용한 이전의 SOTA보다 훨씬 우수하다.
따라서, 우리는 메시 표현이 이 방향의 다음 큰 것이라고 생각하며, 우리의 연구에서 발견된 주요 구성 요소가 단일 이미지에서 직접 3D 메시 재구성을 더욱 발전시키는 후속 작업을 지원할 수 있기를 바란다.
Future work
우리의 방법은 초기 메시와 동일한 토폴로지를 가진 메시만 생성한다.
향후에는 장면 수준 재구성과 같은 보다 일반적인 경우로 접근 방식을 확장하고 다중 뷰 재구성을 위한 여러 이미지에서 배울 것이다.