2022. 3. 18. 14:53ㆍ3D Vision
DeepSDF: Learning Continuous Signed Distance Functions for Shape Representation
Jeong Joon Park, Peter Florence, Julian Straub, Richard Newcombe, Steven Lovegrove

Abstract
컴퓨터 그래픽스, 3D 컴퓨터 비전 및 로봇 커뮤니티는 렌더링 및 재구성을 위해 3D 기하학을 표현하기 위한 여러 가지 접근 방식을 제시했습니다.
이러한 기능은 충실도, 효율성 및 압축 기능을 균형 있게 제공합니다.
본 연구에서는 부분적이고 노이즈가 많은 3D 입력 데이터에서 고품질 형상 표현, 보간 및 완성을 가능하게 하는 도형 클래스의 학습된 연속 부호 거리 함수(SDF) 표현인 DeepSDF를 소개한다.
DeepSDF는 기존의 것과 마찬가지로 연속 부피 필드를 사용하여 형상의 표면을 나타냅니다: 필드의 점의 크기는 표면 경계까지의 거리를 나타내며, 부호는 영역이 형상의 내부(-) 또는 외부(+)에 있는지 여부를 나타냅니다, 따라서 우리의 표현은 공간의 분류를 도형 내부의 일부로 명시적으로 나타내면서 학습된 함수의 제로 레벨 집합으로 도형의 경계를 암묵적으로 부호화한다.
분석 또는 이산 복셀 형식의 기존 SDF는 일반적으로 단일 형상의 표면을 나타내지만 DeepSDF는 전체 형상의 클래스를 나타낼 수 있습니다.
또한 학습된 3D 형상 표현 및 완성도를 위한 SOTA 성능을 보여주면서 이전 작업보다 모델 크기를 차수만큼 줄였습니다.
1. Introduction
이미지 기반 접근법의 주축인 심층 컨볼루션 네트워크는 세 번째 공간 차원으로 직접 일반화하면 시공간의 복잡성에서 빠르게 성장한다, 그리고 삼각형이나 쿼드 메쉬와 같은 보다 클래식하고 콤팩트한 표면 표현은 학습에서 문제를 일으킨다, 왜냐하면 우리는 알려지지 않은 수의 정점과 임의의 토폴로지를 다룰 필요가 있을 수 있기 때문이다.
이러한 어려움으로 인해 처리를 위해 3D 데이터를 입력하거나 객체 분할 및 재구성을 위해 3D 추론을 생성할 때 딥러닝 접근 방식의 품질, 유연성 및 충실도가 제한되었습니다.
본 연구에서는 효율적이고 표현력이 뛰어나며 완전히 연속적인 생성 3D 모델링을 위한 새로운 표현과 접근 방식을 제시합니다.
우리의 접근 방식은 SDF의 개념을 사용하지만, 평가 및 측정 노이즈 제거를 위해 SDF를 일반 그리드로 분해하는 일반적인 표면 재구성 기법과 달리, 우리는 그러한 연속 필드를 생성하기 위한 생성 모델을 학습한다.
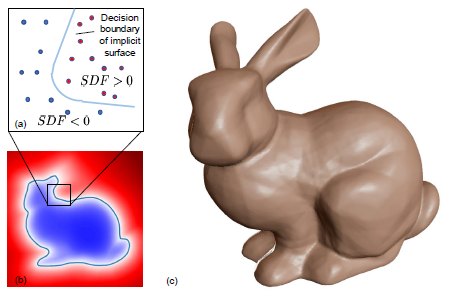
제안된 연속 표현은 그림 2와 같이 의사결정 경계가 형상 자체의 표면인 학습된 형상 조건 분류기로 직관적으로 이해할 수 있다.
우리의 접근 방식은 3D의 복잡한 모양 분포에 잠재 공간을 매핑하려는 다른 작품의 생성적 측면을 공유하지만[54] 중심 표현에서는 결정적으로 다르다.
SDF로 정의되는 암묵적 표면의 개념은 컴퓨터 비전 및 그래픽 커뮤니티에서 널리 알려져 있지만, SDF의 지속적이고 일반화 가능한 3D 생성 모델을 직접 학습하려는 이전 연구는 없습니다.
우리의 기여는 다음과 같습니다: (i) 연속적인 암묵적 표면을 가진 생성 형상 조건부 3D 모델링의 공식화, (ii) 확률론적 자동 디코더에 기초한 3D 형상에 대한 학습 방법, (ii) 형상 모델링과 완성도에 대한 이 공식의 시연과 적용.
우리의 모델은 복잡한 토폴로지를 가진 고품질의 연속 표면을 생산하고 형상 재구성 및 완성도를 정량적으로 비교한 최첨단 결과를 얻습니다.
방법의 효과성의 예로서, 모델에서는 전체 형상 클래스(3D 의자 모델 등)를 나타내기 위해 7.4MB(메가바이트)의 메모리만 사용합니다, 이는 예를 들어 압축되지 않은 단일 512^3 3D 비트맵의 메모리 공간(16.8MB)의 절반에도 미치지 못합니다.
2. Related Work
관련 작업의 세 가지 주요 영역인 형상 학습을 위한 3D 표현(섹션 2.1), 생성 모델을 학습하는 기술(섹션 2.2), 형상 완성(섹션 2.3)을 검토한다.
2.1. Representations for 3D Shape Learning
데이터 기반 3D 학습 접근법에 대한 표현은 크게 세 가지 범주로 분류할 수 있습니다: 포인트 기반, 메시 기반 및 복셀 기반 방법
3D 포인트 클라우드 기반 객체 분류와 같은 일부 애플리케이션은 이러한 표현에 매우 적합하지만, 복잡한 토폴로지로 연속적인 표면을 표현하는 데 있어 한계를 해결합니다.
Point-based.
포인트 클라우드는 많은 센서(예: LiDAR, depth 카메라)가 제공하는 원시 데이터와 매우 가까운 경량 3D 표현이므로 3D 학습을 적용하는 데 자연스럽게 적합합니다.
예를 들어 PointNet [38, 39]는 max-pool 연산을 사용하여 글로벌 형상 특징을 추출하고 있으며, 이 기술은 포인트 생성 네트워크의 인코더로서 널리 사용되고 있다[57, 1].
포인트 클라우드에 대한 학습의 PointNet 스타일 접근법에 관련된 많은 연구가 있습니다.
그러나 포인트 클라우드 학습의 주요 한계는 토폴로지를 기술하지 않고 방수 표면을 생성하는 데 적합하지 않다는 것이다.
Mesh-based.
다양한 접근방식은 미리 정의된 템플릿 메시로 변형 가능한 인체 부분과 같은 유사한 형태의 객체의 클래스를 나타내며, 이러한 모델 중 일부는 높은 충실도 형상 생성 결과를 보여준다[2,34].
다른 최근 연구[3]에서는 형상 최적화를 위해 폴리-큐브 매핑[51]을 사용합니다.
템플릿 메쉬의 사용은 편리하고 자연스럽게 3D 대응 기능을 제공하지만, 고정된 메쉬 토폴로지로만 형상을 모델링할 수 있습니다.
다른 메시 기반 방법에서는 기존 [48, 36] 또는 학습된 [22, 23] 매개 변수화 기술을 사용하여 2D 평면을 모핑하여 3D 표면을 기술합니다.
이러한 표현의 품질은 입력 메쉬 품질과 절단 전략에 민감한 파라미터화 알고리즘에 따라 달라집니다.
이를 해결하기 위해, 최근의 데이터 중심 접근법[57, 22]은 심층 네트워크를 통한 매개 변수화 태스크를 학습합니다.
그러나 그들은 (a) 복잡한 토폴로지를 기술하기 위해 여러 평면이 필요하지만 (b) 생성된 표면 패치는 스티치되지 않는다. 즉, 생성된 형상이 닫히지 않는다고 보고한다.
닫힌 메쉬를 생성하기 위해 구 매개 변수화 [22, 23]를 사용할 수 있지만 결과 형상은 토폴로지 구로 제한됩니다.
메시에 대한 학습과 관련된 다른 연구는 메시[17, 53] 또는 일반 그래프[9]에 새로운 컨볼루션 및 풀링 연산을 사용할 것을 제안한다.
Voxel-based.
3D 가치 그리드를 사용하여 비모수적으로 볼륨을 설명하는 복셀은 2D 이미지 영역에서 탁월했던 잘 알려진 학습 패러다임(즉, 컨볼루션)의 3D 영역으로의 가장 자연스러운 확장일 것입니다.
복셀 기반 학습의 가장 간단한 변형은 밀도 높은 점유 그리드(점유/점유하지 않음)를 사용하는 것이다.
그러나 입방체적으로 증가하는 컴퓨팅 및 메모리 요구 사항으로 인해 현재 방법은 낮은 해상도(128^3 이하)만을 처리할 수 있습니다.
따라서 복셀 기반 접근법은 미세한 형상 세부사항[56, 14]을 보존하지 않으며, 추가적으로 복셀은 렌더링할 때 평활하지 않기 때문에 고충실도 형상과 시각적으로 크게 다르게 나타난다.
Octree 기반 방법[52, 43, 26]은 고밀도 복셀 방법의 계산 및 메모리 한계를 완화하여 예를 들어 최대 512^3 해상도로 학습할 수 있는 능력을 확장하지만, 이 해상도조차도 시각적으로 매력적인 형상을 만들어 내는 것과는 거리가 멀다.
점유 그리드 외에도, 그리고 우리의 접근 방식과 더 밀접하게 관련되어 있으며, 복셀의 3D 그리드를 사용하여 부호화된 거리 함수를 나타낼 수도 있습니다.
이는 [15, 37]에서 개척한 truncated SDF(TSDF)를 활용하여 노이즈 depth 맵을 단일 3D 모델로 결합하는 융합 접근법의 성공을 계승합니다.
Voxel 기반 SDF 표현은 3D 형상 학습[59, 16, 49]에 광범위하게 사용되었지만 이산 복셀을 사용하는 것은 메모리 면에서 비용이 많이 듭니다.
그 결과, 학습된 이산 SDF 접근방식은 일반적으로 저해상도 형상을 나타낸다.
[30]은 거리 필드 압축을 위한 다양한 웨이브릿 변환 기반 접근방식을 보고하는 반면, [10]은 이산 TSDF 볼륨에 차원 축소 기법을 적용한다.
이러한 방법은 도형의 데이터 집합이 아니라 각 개별 장면의 SDF 볼륨을 인코딩합니다.
2.2 Representation Learning Techniques
현대 표현 학습 기법은 데이터를 간결하지만 표현적으로 설명하는 일련의 특징을 자동으로 발견하는 것을 목표로 합니다.
이 분야에 대한 보다 광범위한 검토는 Bengio et al. [4]을 참조한다.
Generative Adversial Networks.
GANs[21]와 그 변형[13, 41]은 발생기에 대해 적대적으로 식별자를 학습시켜 표적 데이터의 심층 임베딩을 학습한다.
이 클래스의 네트워크[29, 31]의 애플리케이션은, 인간, 물체, 또는 장면의 리얼한 이미지를 생성합니다.
단점으로는, GANs에 대한 적대적 학습이 불안정한 것으로 알려져 있다.
3D 영역에서 Wu et al. [54]은 복셀 표현에서 객체를 생성하도록 GAN을 학습시키는 반면, Hamu et al. [23]의 최근 연구는 위상 구체의 형상을 생성하기 위해 다중 매개변수화 평면을 사용한다.
Auto-encoders.
오토 인코더 출력은 인코더와 디코더 사이의 정보 병목 현상의 제약을 고려하여 원래 입력을 복제할 것으로 예상됩니다.
피처 학습 툴로서의 오토 인코더의 능력은 표현 학습을 위해 오토 인코더를 채택한 문헌[16, 49, 2, 22, 55]의 다양한 3D 형상 학습 작업에서 입증되었습니다.
최근 3D 비전 작업[6, 2, 34]은 종종 병목 현상이 가우스 노이즈로 교란되어 부드럽고 완전한 잠재 공간을 장려하는 가변 오토 인코더(VAE) 학습 체계를 채택한다.
잠재 벡터에 대한 정규화는 경사 강하 또는 무작위 샘플링으로 매립 공간을 탐색할 수 있게 한다.
Optimizing Latent Vectors.
표현 학습에 완전한 오토 인코더를 사용하는 대신, 다른 대안은 디코더 전용 네트워크를 훈련시켜 콤팩트한 데이터 표현을 학습하는 것입니다.
이 아이디어는 적어도 역전파를 통해 각 데이터 포인트와 디코더 가중치에 할당된 잠재 벡터를 동시에 최적화하는 Tan et al. [50의 작업으로 거슬러 올라간다.
추론을 위해 새로운 관찰과 고정 디코더 파라미터를 일치시키기 위해 최적의 잠재 벡터를 탐색한다.
유사한 접근방식은 [42, 8, 40]에서 노이즈 감소, 측정 누락 완료 및 고장 감지를 포함한 애플리케이션에 대해 광범위하게 연구되었습니다.
최근의 접근 방식[7, 20]은 심층 아키텍처를 적용하여 기술을 확장합니다.
이 문서에서는 네트워크의 이 클래스를 자동 디코더라고 부릅니다, 이러한 클래스는 디코더만의 아키텍처에서 자기 재구축 손실이 발생하는 훈련을 받고 있기 때문입니다.
2.3. Shape Completion
3D 형상 완성 관련 작업은 희박하거나 부분적인 입력 관측치가 주어진 원래 형상의 보이지 않는 부분을 추론하는 것을 목표로 한다.
이 작업은 2D 컴퓨터 비전에서의 이미지 인화와는 무관합니다.
기존의 표면 재구성 방법은 암시적 표면 함수를 근사하기 위해 방사형 기준 함수(RBF)[11]를 적합시키거나 방향성 포인트 클라우드에서 재구성을 포아송 문제로 캐스팅하여 포인트 클라우드를 조밀한 표면에 완성한다[32].
이러한 방법은 데이터 집합이 아닌 단일 모양만 모델링합니다.
최근 다양한 방법에서는 3D 완성 작업에 데이터 기반 접근 방식을 사용합니다.
이러한 방법의 대부분은 점유 복셀[56], 이산 SDF 복셀[16], depth 맵[44], RGB 이미지[14, 55] 또는 포인트 클라우드[49]의 부분 입력을 잠재 벡터로 저감하고, 그 후 학습된 선험에 근거해 완전한 체적 형상의 예측을 생성하기 위해 인코더/디코더 아키텍처를 채택한다.
3. Modeling SDFs with Neural Networks
이 섹션에서는 지속적인 형상 학습 접근 방식인 DeepSDF에 대해 설명합니다.
모델링 형상을 SDF를 나타내도록 훈련된 피드 포워드 네트워크의 제로 ISO 표면 결정 경계로 설명합니다.
부호 거리 함수는 주어진 공간 점에 대해 점이 방수 표면의 내부(음) 또는 외부(양)에 있는지 여부를 부호화하는 가장 가까운 표면에 대한 점의 거리를 출력하는 연속 함수입니다:
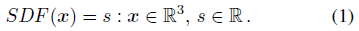
기초 표면은 암묵적으로 SDF(·) = 0의 isosurface으로 표현된다.
이 암묵적인 표면의 뷰는 예를 들어 행진 큐브를 사용하여 얻은 메쉬의 레이캐스팅 또는 래스터라이즈를 통해 렌더링할 수 있다[35].
우리의 핵심 아이디어는 심층 신경망을 사용하여 포인트 샘플에서 연속 SDF를 직접 회귀시키는 것이다.
결과적으로 훈련된 네트워크는 주어진 쿼리 위치의 SDF 값을 예측할 수 있으며, 여기서 공간 샘플을 평가하여 제로 레벨 세트 표면을 추출할 수 있다.
이러한 표면 표현은 그림 2와 같이 결정 경계가 형상 자체의 표면인 학습된 이진 분류기로 직관적으로 이해할 수 있다.
범용 함수 근사치[27]로서 이론상 딥 피드포워드 네트워크는 완전 연속 형상 함수를 임의의 정밀도로 학습할 수 있다.
그러나 실제 근사치의 정밀도는 제한된 계산 능력으로 인해 결정 경계를 안내하는 유한한 점 샘플 수와 네트워크의 유한한 용량에 의해 제한됩니다.
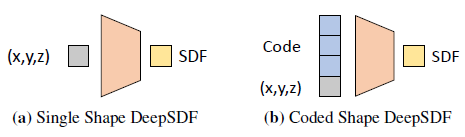
이 접근방식의 가장 직접적인 적용은 그림 3 (a)에 나타낸 것과 같이 주어진 목표 형태에 대해 단일 심층 네트워크를 학습시키는 것이다.
대상 모양이 지정되면 3D 점 샘플과 해당 SDF 값으로 구성된 X 세트 쌍을 준비합니다:
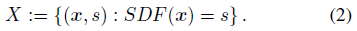
학습 세트 S에서 다층 완전 연결 신경망의 매개변수 θ를 훈련하여 f_θ를 대상 도메인 Ω에서 주어진 SDF의 좋은 근사치로 만든다:
학습은 다음 L1 손실 함수에서 X에 있는 점의 예측 SDF 값과 실제 SDF 값 사이의 손실 합계를 최소화함으로써 수행됩니다:
여기서 clamp(x, δ) := min(δ, max(-δ, x))는 메트릭 SDF를 유지할 것으로 예상되는 표면으로부터의 거리를 제어하기 위해 파라미터 δ를 도입합니다.
δ값이 클수록 각 샘플이 안전한 단계 크기의 정보를 제공하므로 빠른 광선 추적이 가능합니다.
δ의 작은 값을 사용하면, 네트워크 용량을 표면 근처의 디테일에 집중할 수 있습니다.
그림 3 (a)와 같은 3D 모델을 생성하기 위해 δ = 0.1과 완전히 연결된 8개의 레이어로 구성된 피드포워드 네트워크를 사용하며, 각 레이어에는 드롭아웃이 적용되어 있습니다.
모든 내부 레이어는 512차원이며 ReLU 비선형성을 가집니다.
SDF 값을 회귀시키는 출력의 비선형성은 tanh입니다.
배치 정규화를 사용하는 훈련이 불안정하다는 것을 발견하고 [28] 대신 체중 정규화 기법을 적용했다[46].
학습에는 Adam 옵티마이저를 사용합니다[33].
일단 학습을 받으면 표면은 암시적으로 f_θ(x)의 제로 iso-surface로 표현되며, 이는 레이캐스팅 또는 마칭 큐브를 통해 시각화할 수 있다.
이 접근법의 또 다른 좋은 특성은 네트워크를 통한 역전파를 통해 공간도함수 ∂f_θ(x)/∂x를 계산함으로써 정확한 규범이 분석적으로 계산될 수 있다는 것이다.
4. Learning the Latent Space of Shapes
각 형태에 대해 특정 신경망을 학습하는 것은 실현가능하지도 않고 매우 유용하지도 않다.
대신, 우리는 다양한 도형을 표현하고, 그 공통의 특성을 발견하여 저차원 잠재 공간에 삽입할 수 있는 모델을 원합니다.
이를 위해 그림 3 (b)와 같이 원하는 형상을 부호화하는 것으로 생각할 수 있는 잠재 벡터 z를 뉴럴 네트워크에 대한 두 번째 입력으로 도입한다.
개념적으로 이 잠재 벡터를 연속 SDF로 표현되는 3D 형상에 매핑합니다.
형식적으로 i에 의해 인데스된 어떤 형상에 대해 f_θ는 이제 잠재 코드 z_i와 쿼리 3D 위치 x의 함수이며 형상의 대략적인 SDF를 출력한다:
네트워크 출력을 잠재 벡터로 조절함으로써 이 공식은 단일 뉴럴 네트워크로 여러 SDF를 모델링할 수 있습니다.
복호화 모델 f_θ가 주어지면 잠재 벡터 z와 관련된 연속면은 마찬가지로 f_θ(z, x)의 판정 경계에 나타나며, 예를 들어 레이캐스팅 또는 마칭 큐브에 의해 형상을 다시 시각화할 수 있다.
다음으로, 형상 코드화된 DeepSDF의 '자동 디코더' 공식을 도입하기 전에 인코더 없는 학습의 사용을 동기 부여한다.
4.1. Motivating Encoder-less Learning
자동 인코더 및 인코더/디코더 네트워크는 병목 현상이 자연스러운 잠재 변수 표현을 형성하는 경향이 있기 때문에 표현 학습에 널리 사용됩니다.
최근 depth 맵 모델링 [6], 얼굴 [2] 및 체형 [34]과 같은 애플리케이션에서 완전한 자동 인코더가 학습되지만, 일부 입력 관찰이 주어진 최적의 잠재 벡터를 검색하는 추론을 위해 디코더만 유지된다.
다만, 학습이 끝난 인코더는 테스트시에 사용되지 않기 때문에, 학습 중에 인코더를 사용하는 것이 계산 자원을 가장 효과적으로 사용하는지는 불명확합니다.
이것은 그림 4와 같이 인코더 없이 형상 매립을 학습하기 위해 자동 디코더를 사용하도록 동기를 부여한다.
연속 SDF를 학습하기 위해 자동 디코더를 적용하면 고품질 3D 생성 모델로 이어진다는 것을 보여준다.
또한, 우리는 개선된 일반화를 위해 잠재 공간 정규화를 자연스럽게 도입하는 자동 디코더 학습 및 테스트를 위한 확률론적 공식을 개발한다.
우리가 아는 한, 이 작업은 자동 디코더 학습 방법을 3D 학습 커뮤니티에 처음 도입한 것입니다.
4.2. Auto-decoder-based DeepSDF Formulation
5. Data Preparation
6. Results
7. Conclusion & Future Work
DeepSDF는 형상 표현 및 완성 작업 전반에 걸쳐 적용 가능한 벤치마크 방법을 크게 능가하며, 형상의 고품질 표면 규범을 제공하면서 복잡한 토폴로지, 닫힌 표면을 표현하는 목표를 동시에 해결합니다.
그러나 도형의 SDF의 점 단위 순방향 샘플링은 효율적인 반면, 잠재 벡터에 대한 명시적 최적화의 필요성 때문에 추론 중에 형상 완료(자동 디코딩)에 상당한 시간이 걸린다.
ADAM 최적화를 모델의 분석적 파생물을 사용하는 보다 효율적인 Gauss-Newton 또는 유사한 방법으로 대체하여 성능을 향상시키려 한다.
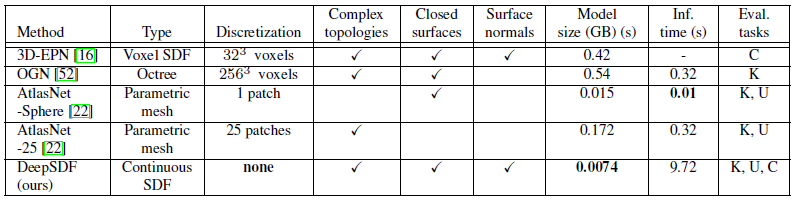
DeepSDF 모델은 표 1에 나온 것과 같이 이전의 최신 결과보다 훨씬 적은 메모리로 더 복잡한 형상을 이산 오류 없이 표현할 수 있도록 지원하여 3D 형상 학습을 위한 흥미로운 경로를 보여줍니다.
고품질의 잠재 형상 공간 보간법을 생성하는 명확한 능력은 이러한 효율적인 인코딩으로 구성된 장면에서 작동하는 재구성 알고리즘의 문을 엽니다.
그러나, DeepSDF는 현재 모델이 표준 포즈이며, 따라서 자연 상태에서 완료하려면 추론 시간을 증가시키는 SE(3) 변환 공간에 대한 명시적 최적화가 필요하다고 가정한다.
마지막으로, 하나의 임베딩으로 역동성과 텍스처를 포함한 가능한 장면의 진정한 공간을 표현하는 것은 여전히 중요한 과제이며, 우리가 계속 탐구해야 할 과제이다.
'3D Vision' 카테고리의 다른 글
| Pyramid Stereo Matching Network (0) | 2022.03.25 |
|---|---|
| Mesh R-CNN (번역) (0) | 2022.03.23 |
| Occupancy Networks: Learning 3D Reconstruction in Function Space (0) | 2022.03.10 |
| Pixel2Mesh : Generating 3D Mesh Models from Single RGB Images (0) | 2022.03.04 |
| PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space (0) | 2022.03.02 |