2022. 3. 29. 18:06ㆍView Synthesis
Mip-NeRF: A Multiscale Representation for Anti-Aliasing Neural Radiance Fields
Jonathan T. Barron, Ben Mildenhall, Matthew Tancik, Peter Hedman, Ricardo Martin-Brualla, Pratul P. Srinivasan
Abstract
Neural Radiance Field (NeRF)에서 사용되는 렌더링 절차는 픽셀당 단일 ray로 장면을 샘플링하므로 학습 또는 테스트 영상이 다른 해상도로 장면 내용을 관찰할 때 지나치게 블러하거나 앨리어스되는 렌더링을 생성할 수 있습니다.
픽셀당 여러 개의 ray를 사용하여 렌더링하여 슈퍼샘플링을 수행하는 간단한 솔루션은 각 ray를 렌더링할 때 멀티 레이어 퍼셉트론을 수백 번 쿼리해야 하므로 NeRF에는 실용적이지 않습니다.
우리가 "mip-NeRF"('mipmap')라고 부르는 우리의 솔루션은 연속적인 가치의 척도로 장면을 표현하도록 NeRF를 확장한다.
mip-NeRF는 ray가 아닌 안티 앨리어스 원뿔형 frustums을 효율적으로 렌더링하여 부적절한 에일리어싱 아티팩트를 줄이고 NeRF의 fine 디테일 표현 능력을 대폭 향상시킵니다, 또한 NeRF보다 속도가 7% 빠르고 크기가 절반입니다.
NeRF와 비교하여 mip-NeRF는 NeRF에 제공된 데이터셋에서 평균 오류율을 17%까지, NeRF에서 제공하는 까다로운 멀티스케일 변형 데이터셋에서 평균 오류율을 60%까지 낮춥니다.
또한 Mip-NeRF는 멀티스케일 데이터셋에서 22배 빠른 속도로 브루트포스 슈퍼샘플링된 NeRF의 정확성과 일치할 수 있습니다.
1. Introduction
Neural Radiance Field (NeRF)[30]와 같은 신경 볼륨 표현은 사진 사실적인 새로운 뷰를 렌더링하기 위해 이미지에서 3D 물체와 장면을 표현하는 방법을 학습하기 위한 매력적인 전략으로 부상했습니다.
NeRF와 그 변형은 다양한 뷰 합성 태스크에서 인상적인 결과를 보여주었지만, NeRF의 렌더링 모델은 과도한 블러링 및 앨리어싱을 유발할 수 있는 방식으로 결함이 있습니다.
NeRF는 입력 5D 좌표(3D 위치 및 2D 뷰 방향)에서 해당 위치의 장면 속성(볼륨 밀도 및 뷰 의존 방사 radiance)으로 매핑되는 다층 퍼셉트론 (MLP)로 매개 변수화된 기존의 이산 샘플링 지오메트리를 연속 볼륨 측정 함수로 대체합니다.
픽셀의 색상을 렌더링하기 위해 NeRF는 해당 픽셀을 통과하여 해당 픽셀의 볼륨 표현에 단일 ray를 캐스팅하고 해당 ray를 따라 샘플의 MLP에 장면 속성을 쿼리하고 이러한 값을 단일 색상으로 합성합니다.
모든 학습 및 테스트 영상이 거의 일정한 거리에서 장면 내용을 관찰할 때 이 접근법이 잘 작동하지만(NeRF 및 대부분의 후속 조치에서 수행됨) NeRF 렌더링은 덜 계획적인 시나리오에서 상당한 아티팩트를 보인다.
학습용 영상이 여러 해상도로 장면 내용을 관찰하는 경우, 복구된 NeRF의 렌더링이 근접 뷰에서 지나치게 블러하게 나타나고 원거리 뷰에서 앨리어싱 아티팩트를 포함합니다.
간단한 해결책은 오프라인 raytracing에서 사용되는 전략을 채택하는 것입니다: 각 픽셀의 차지하는 공간을 여러 개의 raytracing으로 슈퍼샘플링하는 것입니다.
그러나 이것은 단일 ray를 렌더링하는 데 수백 개의 MLP 평가가 필요하고 단일 장면을 재구성하는 데 몇 시간이 걸리는 NeRF와 같은 신경 체적 표현에는 엄청나게 비싸다.
이 논문에서는 컴퓨터 그래픽 렌더링 파이프라인에서의 에일리어싱을 방지하기 위해 사용되는 mipmapping 접근법에서 영감을 얻습니다.
mipmap은 서로 다른 이산 다운샘플링 스케일 세트의 신호(일반적으로 이미지 또는 텍스처 맵)를 나타내며 해당 ray와 교차하는 형상에 대한 픽셀이 차지하는 공간의 투영에 기초하여 ray에 사용할 적절한 축척을 선택합니다.
이 전략은 안티 에일리어싱의 계산 부하가 렌더링 시간(브루트포스 슈퍼샘플링 솔루션과 마찬가지로)에서 프리컴퓨팅 단계로 이행하기 때문에 프리필터링이라고 불립니다, mipmap은 렌더링 횟수에 관계없이 특정 텍스처에 대해 1회만 작성하면 됩니다.

mip-NeRF("mipmap"에서와 같이, multum in parvo NeRF)라고 하는 솔루션은 연속적인 스케일 공간에 대해 사전 필터링된 radiance 필드를 동시에 나타내도록 NeRF를 확장합니다.
mip-NeRF에 대한 입력은 3D 가우시안이며, radiance 필드를 통합해야 하는 영역을 나타냅니다.
그림 1에 나타낸 것처럼 mip-NeRF를 원뿔을 따라 간격을 두고 쿼리하여 프리필터링된 픽셀을 렌더링할 수 있습니다.
3D 위치와 그 주변의 가우시안 영역을 인코딩하기 위해 새로운 피쳐 표현인 Integrated Positional Encoding (IPE)을 제안한다.
이는 공간의 단일 지점이 아닌 공간 영역을 콤팩트하게 피처화할 수 있는 NeRF의 Positional Encoding (PE)의 일반화입니다.

Mip-NeRF는 NeRF의 정확성을 크게 개선하며, 이러한 이점은 장면 내용이 다른 해상도로 관찰되는 상황(즉, 카메라가 장면에서 점점 더 가까이 이동하는 설정)에서 훨씬 더 크다.
우리가 제시하는 까다로운 다중 해상도 벤치마크에서 mip-NeRF는 NeRF에 비해 오류율을 평균 60%까지 줄일 수 있다(시각화는 그림 2 참조).
또한 Mip-NeRF의 스케일 인식 구조를 통해 계층형 샘플링 [30]에 NeRF에 의해 사용되는 개별 "coarse" 및 "fine" MLP를 단일 MLP로 병합할 수 있습니다.
그 결과 mip-NeRF는 NeRF(~7%)보다 약간 빠르며 파라미터의 절반을 가진다.
2. Related Work
우리의 작업은 관찰된 이미지에서 3D 장면 표현을 학습하여 새로운 사진 사실적 뷰를 합성하는 매우 영향력 있는 기술인 NeRF[30]를 직접 확장합니다.
여기서는 샘플링과 에일리어싱에 중점을 두고 컴퓨터 그래픽과 뷰 합성에 사용되는 3D 표현을 검토한다, 여기에는 NeRF와 같은 최근 도입된 연속 신경 표현이 포함된다.
Anti-aliasing in Rendering
샘플링과 앨리어싱은 컴퓨터 그래픽스의 렌더링 알고리즘 개발 전반에 걸쳐 광범위하게 연구되어 온 근본적인 문제입니다.
앨리어싱 아티팩트("안티-에일리어싱")는 일반적으로 슈퍼샘플링 또는 프리필터를 통해 감소됩니다.
슈퍼샘플링 기반 기술[46]은 나이키스트 주파수에 더 가까운 샘플을 추출하기 위해 렌더링하는 동안 픽셀당 여러 개의 ray를 조사합니다.
이는 에일리어싱을 줄이기 위한 효과적인 전략이지만 런타임은 일반적으로 슈퍼샘플링 속도에 따라 선형적으로 확장되기 때문에 비용이 많이 듭니다.
따라서 슈퍼샘플링은 일반적으로 오프라인 렌더링 컨텍스트에서만 사용됩니다.
프리필터링 기반 기술은 나이키스트 주파수와 일치하도록 더 많은 ray를 샘플링하는 대신 로우패스 필터링된 버전의 장면 콘텐츠를 사용하여 앨리어스 없이 장면을 렌더링하는 데 필요한 나이키스트 주파수를 줄입니다.
프리필터링 기술[18, 20, 32, 49]은, 장면 컨텐츠의 필터링된 버전을 미리 계산할 수 있기 때문에, 렌더링시에 타겟 샘플링 비율에 따라 올바른 "스케일"을 사용할 수 있기 때문에, 실시간 렌더링에 보다 적합합니다.
렌더링의 맥락에서 프리필터는 각 픽셀[1, 16]을 통과하는 ray가 아닌 원뿔을 추적하는 것으로 생각할 수 있다: 원뿔이 장면 컨텐츠와 교차하는 장소에서는 미리 계산된 멀티스케일 표현(예를 들어 sparse voxel octree[15, 21] 또는 mipmap [47])이 원뿔의 차지하는 공간에 대응하는 스케일로 조회된다.
우리의 작업은 이 그래픽 작업 라인에서 영감을 얻어 NeRF를 위한 멀티스케일 장면 표현을 제공합니다.
우리의 전략은 두 가지 중요한 면에서 기존의 그래픽 파이프라인에서 사용되는 멀티스케일 표현과 다르다.
첫째, 문제의 설정에서는 장면의 지오메트리를 사전에 알 수 없기 때문에 멀티스케일 표현을 사전에 계산할 수 없습니다 - 이미 정의된 CGI 자산을 렌더링하지 않고 컴퓨터 비전을 사용하여 장면의 모델을 복구하고 있습니다.
따라서 Mip-NeRF는 학습 중에 장면의 사전 필터링된 표현을 학습해야 합니다.
둘째, 스케일에 대한 우리의 개념은 이산적인 것이 아니라 연속적입니다.
mip-NeRF는 (mipmap과 같이) 고정된 수의 척도로 여러 복사본을 사용하여 장면을 표현하는 대신 임의 척도로 쿼리할 수 있는 단일 신경 장면 모델을 학습합니다.
Scene Representations for View Synthesis
뷰 합성 작업에 대해 다양한 장면 표현이 제안되었습니다: 관찰되지 않은 카메라 시점에서 장면의 새로운 사진 사실적 이미지를 렌더링하는 것을 지원하는 장면의 관찰된 이미지를 사용하여 표현을 복구합니다.
장면의 이미지가 조밀하게 캡처되면 라이트 필드 보간 기법[9, 14, 22]을 사용하여 장면의 중간 표현을 재구성하지 않고 새로운 뷰를 렌더링할 수 있습니다.
샘플링 및 앨리어싱과 관련된 문제는 이 설정 내에서 철저히 연구되었다[7].
드물게 캡처된 영상에서 새로운 뷰를 합성하는 방법은 일반적으로 장면의 3D 지오메트리 및 모양을 explicit 재구성합니다.
많은 고전적인 뷰 합성 알고리즘은 확산 [28] 또는 뷰 의존 [6, 10, 48] 텍스처와 함께 메시 기반 표현을 사용합니다.
메시 기반 표현은 효율적으로 저장할 수 있으며 기존 그래픽 렌더링 파이프라인과 자연스럽게 호환됩니다.
그러나, 메시 지오메트리와 토폴로지를 최적화하기 위해 그라데이션 기반 방법을 사용하는 것은 비연속성과 로컬 최소값으로 인해 일반적으로 어렵습니다.
따라서 뷰 합성을 위해 체적 표현이 점점 더 인기를 끌고 있다.
초기 접근법은 관찰된 이미지를 사용하여 복셀 그리드에 직접 색을 입히고[37], 보다 최근의 볼륨 측정 접근법은 그래디언트 기반 학습을 사용하여 심층 네트워크를 학습시켜 장면의 복셀 그리드 표현을 예측한다[12, 25, 29, 38, 41, 53].
이산 복셀 기반 표현은 뷰 합성에 효과적이지만 더 높은 해상도의 장면에는 잘 조정되지 않습니다.
컴퓨터 비전 및 그래픽 연구의 최근 동향은 이러한 개별 표현을 좌표 기반 신경 표현으로 대체하는 것입니다, 이 표현은 3D 좌표에서 해당 위치의 장면 속성에 매핑되는 MLP에 의해 매개 변수화된 연속 함수로 표현됩니다.
일부 최근 방법은 좌표 기반 신경 표현을 사용하여 장면을 implicit 표면으로 모델링[31, 50]하지만, 최근 뷰 합성 방법의 대부분은 체적 NeRF 표현[30]에 기초한다.
NeRF는 생성 모델링[8, 36], 동적 장면[23, 33], 비강성 변형 물체[13, 34], 조명과 방해물이 변화하는 phototourism 설정[26, 43], 재조명을 위한 반사 모델링[2, 3, 40]에 대한 연속 신경 체적 표현을 확장하는 많은 후속 작업에 영감을 주었다.
좌표 기반 신경 표현을 사용하여 뷰 합성의 맥락에서 샘플링과 앨리어싱 문제에 상대적으로 거의 관심을 기울이지 않았다.
폴리곤 메쉬 및 복셀 그리드와 같은 뷰 합성에 사용되는 이산 표현은 mipmap 및 octree와 같은 기존의 멀티스케일 프리필터링 방식을 사용하여 앨리어스 없이 효율적으로 렌더링할 수 있습니다.
그러나 뷰 합성을 위한 좌표 기반 신경 표현은 현재 슈퍼샘플링을 통해서만 안티 앨리어싱이 가능하며, 이는 이미 느린 렌더링 절차를 악화시킨다.
Takikawa et al. [42]의 최근 작품은 implicit 표면의 연속 신경 표현을 위해 sparse voxel octree에 기초한 멀티스케일 표현을 제안하지만, 그 접근법은 유일한 입력이 관찰된 이미지인 뷰 합성 설정과 달리 장면 지오메트리를 선험적으로 알아야 한다.
Mip-NeRF는 이 미해결 문제에 대처하고 학습과 테스트 모두에서 안티 앨리어스 이미지를 효율적으로 렌더링할 수 있을 뿐만 아니라 학습 중 멀티스케일 이미지를 사용할 수 있습니다.
2.1. Preliminaries: NeRF
NeRF는 다층 퍼셉트론 (MLP)의 가중치를 사용하여 장면을 차단하고 방출하는 입자의 연속 부피 필드로 나타냅니다.
NeRF는 카메라의 각 픽셀을 다음과 같이 렌더링합니다: ray r(t) = o + td는 픽셀을 통과하도록 카메라의 투영 중심 o에서 d 방향을 따라 방출된다.
샘플링 전략(나중에 설명)은 카메라의 사전 정의된 근면과 원면 t_n 및 t_f 사이의 정렬된 거리 t의 벡터를 결정하기 위해 사용됩니다.
각 거리 t_k ∈ t에 대해 ray x = r(t_k)를 따라 해당하는 3D 위치를 계산한 다음 위치 인코딩을 사용하여 각 위치를 변환한다:

이것은 단순히 1에서 2^(L-1)까지 2의 거듭제곱으로 스케일링된 3D 위치 x의 각 차원의 사인 및 코사인 연결입니다, 여기서 L은 하이퍼 파라미터입니다.
NeRF의 충실도는 장면을 매개 변수화하는 MLP가 보간 함수로 동작할 수 있기 때문에 위치 인코딩의 사용에 따라 결정적으로 좌우된다(자세한 내용은 Tancik et al. [44] 참조).
각 ray 위치 γ(r(t_k))의 위치 부호화는 밀도 τ 및 RGB 색상 c를 출력하는 가중치 Θ에 의해 파라미터화된 MLP에 대한 입력으로 제공됩니다:

또한 MLP는 뷰 방향을 입력으로 사용합니다, 이것은 단순화를 위해 표기법에서 생략됩니다.
이러한 추정 밀도와 색상은 Max [27]에 따라 수치 직교법을 사용하여 볼륨 렌더링 적분을 근사하는 데 사용됩니다:

여기서 C(r; Θ, t)는 픽셀의 최종 예측 색상입니다.
Θ로 파라미터화된 NeRF를 렌더링하는 이 절차를 통해 NeRF를 학습하는 것은 간단합니다: 카메라 포즈로 관찰된 이미지 세트를 사용하면 경사 강하를 사용하여 모든 입력 픽셀 값과 모든 예측 픽셀 값 사이의 제곱 차이의 합을 최소화할 수 있습니다.
샘플 효율을 개선하기 위해 NeRF는 파라미터 Θ^c와 Θ^f를 사용하여 2개의 개별 MLP를 학습합니다, 하나는 "coarse"이고 다른 하나는 "fine"입니다:

여기서 C*(r)는 입력 이미지에서 가져온 관찰된 픽셀 색이며, R은 모든 이미지에 걸친 모든 pixels/rays 세트입니다.
Mildenhall et al. 은 층화 표본 추출을 통해 균일한 간격의 랜덤 t 값 64개를 샘플링하여 t^c를 구축한다.
그 후, "coarse" 모델에 의해 생성된 합성 가중치 w_k = T_k(1 - exp(-τ_k(t_(k+1) - t_k))를 가시 장면 컨텐츠의 분포를 기술하는 부분 상수 PDF로서 받아들여, 그 PDF로부터 128개의 새로운 t값을 추출해 t^f 를 생성한다.
그런 다음 이 192 t 값의 결합을 정렬하여 "fine" MLP로 전달하여 최종 예측 픽셀 색상을 생성합니다.
3. Method
논의된 바와 같이, NeRF의 포인트 샘플링은 샘플링 및 앨리어싱과 관련된 문제에 취약하게 만든다: 픽셀의 색상은 픽셀의 frustum 내에서 들어오는 모든 radiance의 적분이지만 NeRF는 픽셀당 하나의 무한히 좁은 ray를 투사하여 앨리어스를 발생시킨다.
Mip-NeRF는 각 픽셀에서 원뿔을 캐스팅하여 이 문제를 개선합니다.
각 ray를 따라 포인트 샘플링을 수행하는 대신 원뿔형 frustum(축에 수직으로 절단된 원뿔)으로 원뿔을 분할합니다.
또, 공간의 극히 작은 포인트로부터 위치 부호화 (PE) 피쳐를 구축하는 대신에, 각 원뿔형 frustum으로 커버되는 볼륨의 Intergrated positional encoding (IPE) 표현을 구축합니다.
이러한 변경에 의해 MLP는 중심뿐만 아니라 각 원뿔형 frustum의 크기와 모양을 추론할 수 있습니다.
규모에 대한 NeRF의 무감각성과 이 문제에 대한 Mip-NeRF의 해결책으로 인한 모호성은 그림 3에 시각화된다.
이러한 원뿔형 frustum 및 IPE 피쳐를 사용하면 NeRF의 두 개의 개별적인 "coarse" 및 "fine" MLP를 단일 멀티스케일 MLP로 줄일 수 있으므로 학습 및 평가 속도가 향상되고 모델 크기가 50% 감소합니다.
3.1. Cone Tracing and Positional Encoding
여기에서는 mip-NeRF의 렌더링 및 피처화 절차에 대해 설명합니다, 여기에서는 원뿔을 캐스팅하고 그 원뿔형 frustum을 따라 피처화합니다.
NeRF와 마찬가지로 mip-NeRF의 이미지는 한 번에 한 픽셀씩 렌더링되므로 렌더링되는 개별 픽셀의 관점에서 절차를 설명할 수 있습니다.
그 픽셀에 대해서, 카메라의 투영 o의 중심으로부터, 픽셀의 중심을 통과하는 방향 d에 따라서 원뿔을 캐스팅했습니다.
이 원뿔의 정점은 o이고 이미지 평면 o + d의 원뿔 반지름은 r˙로 파라미터화됩니다.
r˙를 2/√12로 스케일링된 월드 좌표의 픽셀 폭에 설정했고, 이는 이미지 평면의 섹션이 픽셀 풋프린트의 분산과 일치하는 x와 y의 분산을 갖는 원뿔을 산출한다.
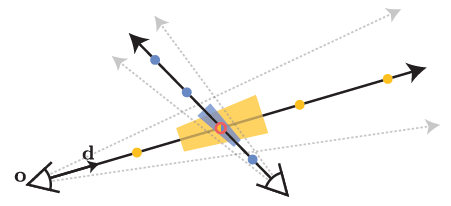
두 t값 [t_0, t_1] 사이의 원뿔형 frustum 내에 있는 위치 x의 집합은 다음과 같다(그림 1에 표시):
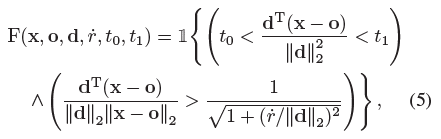
여기서 1{·}은 지시함수이다: x가 (o, d, r˙, t_0, t_1)에 의해 정의된 원뿔형 frustum 내에 있는 경우 F(x, ·) = 1.
우리는 이제 이 원뿔형 frustum 안에 있는 볼륨의 피쳐화된 표현을 구성해야 한다.
Mildenhall et al.이 이 피쳐 표현이 NeRF의 성공에 중요하다는 것을 보여주듯이, 이러한 피쳐화된 표현은 NeRF에서 사용되는 위치 부호화 피쳐와 유사한 형태여야 한다[30].
여기에는 많은 실행 가능한 접근법이 있지만(자세한 내용은 부록 참조), 우리가 발견한 가장 간단하고 효과적인 해결책은 원뿔형 좌표에 있는 모든 좌표의 예상되는 위치 부호화를 단순히 계산하는 것이었다:
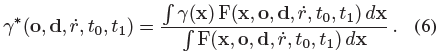
그러나 분자의 적분에는 닫힌 형태의 해답이 없기 때문에 그러한 피쳐가 어떻게 효율적으로 계산될 수 있을지는 불분명하다.
따라서 우리는 "integrated positional encoding" (IPE)라고 하는, 원하는 피쳐에 대한 효율적인 근사치를 가능하게 하는 다변량 가우시안을 사용하여 원뿔형 frustum을 근사한다.
다변량 가우시안에서 원뿔형 frustum을 근사하려면 F(x, ·)의 평균과 공분산을 계산해야 한다.
각 원뿔형 frustum은 원형으로 간주되며 원뿔형 frustum은 원뿔형 축을 중심으로 대칭이기 때문에 이러한 가우시안 값은 (o 및 d 외에) 세 가지 값으로 완전히 특징지어진다: ray μ_t에 따른 평균 거리, ray σ_t^2에 따른 분산, 및 ray에 수직인 분산 σ_r^2:
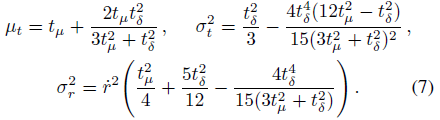
이들 양은 수치 안정성에 중요한 중간점 t_μ = (t_0 + t_1)/2 및 반폭 t_δ = (t_1 - t_0)/2에 대해 파라미터화된다.
자세한 내용은 부록을 참조하십시오.
이 가우시안을 원뿔형 frustum의 좌표 프레임에서 다음과 같이 월드 좌표로 변환할 수 있습니다:
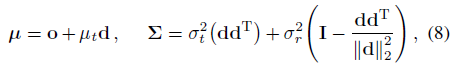
최종 다변량 가우시안 값을 제공합니다.
다음으로 IPE를 도출한다, IPE는 앞서 언급한 가우시안 분포에 따라 위치 부호화된 좌표에 대한 기대치이다.
이를 수행하려면 먼저 식 1의 PE를 푸리에 피쳐[35, 44]로 다시 쓰는 것이 좋습니다:
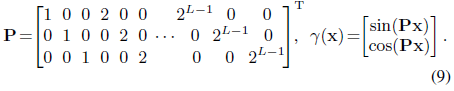
이 재파라미터화를 통해 IPE의 닫힌 형식을 도출할 수 있습니다.
변수의 선형 변환의 공분산이 변수의 공분산(Cov[Ax, By] = A Cov[x,y]B^T)의 선형 변환이라는 사실을 사용하여 PE basis P로 들어 올린 후 원뿔형 frustum 가우시안의 평균과 공분산을 식별할 수 있다:
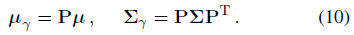
IPE 피쳐를 생성하는 마지막 단계는 이 들어올린 다변량 가우시안에 대한 기대치를 계산하는 것입니다, 이 가우시안은 사인 및 코사인 위치에 따라 변조됩니다.
이러한 기대에는 단순한 폐쇄형 표현이 있습니다:
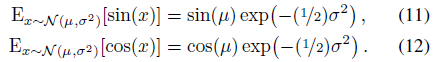
이 예상 사인 또는 코사인은 단순히 분산의 가우시안 함수에 의해 감쇠된 평균의 사인 또는 코사인임을 알 수 있습니다.
이를 통해 최종 IPE 피쳐를 평균의 예상 사인 및 코사인 및 공분산 행렬의 대각선으로 계산할 수 있습니다:
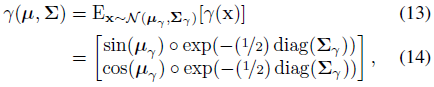
여기서 ◦는 요소별 곱셈을 나타냅니다.
위치 부호화는 각 차원을 독립적으로 부호화하기 때문에 이 예상되는 부호화는 γ(x)의 한계 분포에만 의존하며, 공분산 행렬의 대각선(차원별 분산의 벡터)만 필요하다.
∑_γ는 비교적 큰 크기 때문에 계산 비용이 많이 들기 때문에 ∑_γ의 대각선을 직접 계산한다:
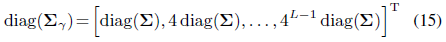
이 벡터는 3D 위치의 공분산 ∑의 대각선에만 의존하며, 다음과 같이 계산할 수 있습니다:
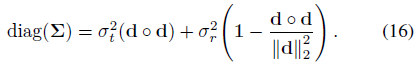
이러한 대각선을 직접 계산할 경우 IPE 피쳐는 PE 피쳐 구축 비용만큼 비용이 많이 듭니다.
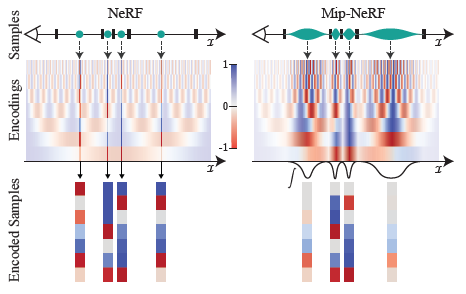
그림 4는 toy 1D 도메인에서 IPE와 기존 PE 피쳐 간의 차이를 시각화합니다.
IPE 피쳐는 직관적으로 동작합니다: 위치 부호화의 특정 주파수에 IPE 피쳐의 구축에 사용되는 간격의 폭보다 큰 기간이 설정되어 있는 경우, 그 주파수에서의 부호화는 영향을 받지 않습니다.
단, 주기가 간격보다 작을 경우(이 경우 해당 간격의 PE가 반복적으로 발진합니다), 해당 주파수의 부호화는 0으로 축소됩니다.
즉, IPE는 일정 간격으로 일정한 주파수를 유지하고 간격에 따라 변화하는 주파수를 부드럽게 "삭제"하는 반면 PE는 모든 주파수를 수동으로 조정된 하이퍼 파라미터 L까지 유지합니다.
이와 같이 각 사인 및 코사인을 스케일링함으로써 IPE 피쳐는 공간 볼륨의 크기와 모양을 매끄럽게 인코딩하는 효과적인 안티 앨리어스 위치 부호화 피쳐가 된다.
또한 IPE는 L을 하이퍼 파라미터로 효과적으로 삭제합니다: L은 단순히 매우 큰 값으로 설정하고 튜닝하지 않을 수 있습니다(부록 참조).
3.2. Architecture
원뿔 트레이스 및 IPE 피쳐를 제외하고 mip-NeRF는 섹션 2.1에서 설명한 바와 같이 NeRF와 유사하게 동작합니다.
렌더링되는 각 픽셀에 대해 NeRF와 같은 ray 대신 원뿔이 캐스팅된다.
ray를 따라 t_k에 대해 n개의 값을 샘플링하는 대신 t_k에 대해 n+1 값을 샘플링하고 앞에서 설명한 것처럼 샘플링된 t_k 값의 각 쌍에 걸친 간격에 대해 IPE 피쳐를 계산합니다.
이러한 IPE 피쳐는 식 2와 같이 밀도 τ_k 및 색상 c_k를 생성하기 위해 MLP에 입력으로 전달됩니다.
mip-NeRF에서의 렌더링은 식 3에 따릅니다.
NeRF는 두 개의 서로 다른 MLP, 즉 하나는 "coarse"와 "fine"를 가진 계층적 샘플링 절차를 사용합니다(식 4 참조).
이것은 NeRF에서 필요했습니다, 왜냐하면 NeRF의 PE 피쳐는 MLP가 단일 스케일에 대해서만 장면의 모델을 학습할 수 있음을 의미했기 때문입니다.
그러나 원뿔 캐스팅 및 IPE 피쳐를 통해 입력 피쳐에 축척을 explicitly 인코딩할 수 있으므로 MLP가 장면의 멀티스케일 표현을 학습할 수 있습니다.
따라서 Mip-NeRF는 파라미터가 Θ인 단일 MLP를 사용합니다, 이러한 MLP는 계층형 샘플링 전략으로 반복적으로 쿼리됩니다.
여기에는 여러 가지 이점이 있습니다, 모델 크기가 반으로 줄고 렌더링이 더 정확하며 샘플링이 더 효율적이며 전체 알고리즘이 더 단순해집니다.
우리의 최적화 문제는 다음과 같습니다:
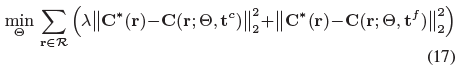
단일 MLP가 있기 때문에 "coarse" loss는 "fine" loss에 대해 균형을 이루어야 합니다, 이 loss는 하이퍼 파라미터 λ를 사용하여 달성됩니다(모든 실험에서 λ = 0.1로 설정).
Mildenhall et al. [30] 성층화 샘플링으로 coarse 샘플 t^c를 생성하고 역변환 샘플링을 사용하여 결과 알파 합성 가중치 w에서 fine 샘플 t^f를 샘플링한다.
fine MLP가 64개의 coarse 샘플과 128개의 fine 샘플로 구분된 결합을 제공하는 NeRF와는 달리 mip-NeRF에서는 단순히 coarse 모델의 샘플 128개와 fine 모델의 샘플 128개를 추출합니다(공정 비교를 위해 NeRF와 동일한 수의 총 MLP 평가를 산출).
t^f를 샘플링하기 전에 가중치 w를 약간 변경합니다:
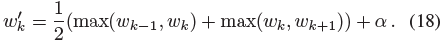
2탭의 최대 필터에 이어 2탭의 블러 필터("blurpool" [51])로 w를 필터링 합니다, 이 필터는 w에 넓고 매끄러운 상부 엔벨로프를 만듭니다.
하이퍼파라미터 α가 1로 다시 정규화되기 전에 해당 엔벨로프에 추가되어 일부 샘플이 빈 공간 영역에서도 추출되도록 한다(모든 실험에서 α = 0.01로 설정).
Mip-NeRF는 JaxNeRF [11] 위에 구현됩니다: JAX [4]의 NeRF 재실행으로 원래 TensorFlow 구현보다 더 나은 정확도를 달성하고 더 빠르게 학습합니다.
우리는 NeRF의 학습 절차를 따른다: 배치 크기가 4096이고 5·10^-4에서 5·10^-6으로 로그적으로 해제되는 학습 속도를 가진 Adam [19]의 100만 번의 반복.
퍼포먼스에 큰 영향을 주지 않고 원뿔 트레이싱, IPE 및 단일 멀티스케일 MLP의 사용에 부수되는 JaxNeRF와 mip-NeRF의 추가 세부사항 및 몇 가지 차이점에 대해서는 부록을 참조해 주십시오.
4. Results
우리는 원래 NeRF 논문[30]에 제시된 Blender 데이터 세트와 다중 해상도 장면에서 정확도를 더 잘 조사하고 이러한 작업에 대한 NeRF의 중요한 취약성을 강조하기 위해 설계된 데이터 세트의 간단한 다중 스케일 변형에서 mip-NeRF를 평가한다.
우리는 NeRF에서 사용되는 PSNR, SSIM [45] 및 LPIPS [52]의 세 가지 오류 메트릭을 보고합니다.
더 쉽게 비교할 수 있도록 MSE = 10^-PSNR/10, √(1 - SSIM) 및 LPIPS의 세 가지 메트릭을 모두 요약하는 "평균" 오류 메트릭도 제시한다.
우리는 NeRF와 mip-NeRF의 각 변형에 대한 네트워크 매개 변수 수뿐만 아니라 런타임(벽 시간의 중위 및 중위 절대 편차)을 추가로 보고한다.
모든 JaxNeRF 및 mip-NeRF 실험은 32개의 코어가 있는 TPU v2에서 학습됩니다 [17].
우리는 NeRF에서 사용하는 원래 Blender 데이터 세트가 미묘하지만 결정적인 약점을 가지고 있기 때문에 멀티스케일 Blender 벤치마크를 구성했다.
즉, 모든 카메라는 동일한 초점거리와 해상도를 가지며 물체로부터 동일한 거리에 배치된다.
결과적으로, 이 Blender 작업은 카메라가 피사체와 더 가깝거나 더 멀리 있거나 확대/축소할 수 있는 대부분의 실제 데이터 세트보다 훨씬 쉽다.
이 데이터 세트의 제한은 NeRF의 한계로 보완된다.
NeRF는 앨리어싱 렌더링을 생성하는 경향에도 불구하고 Blender 데이터 세트에서 우수한 결과를 생성할 수 있다, 왜냐하면 이 데이터 세트는 체계적으로 이 실패 모드를 피하기 때문이다.
Multiscale Blender Dataset
우리의 다중 스케일 Blender 데이터 세트는 앨리어싱 및 스케일 공간 추론을 조사하기 위해 설계된 NeRF의 Blender 데이터 세트에 대한 간단한 수정이다.
이 데이터 세트는 Blender 데이터 세트의 각 이미지를 가져와서 2, 4, 8의 팩터를 박스 다운 샘플링하고(그리고 그에 따라 카메라 intrinsic 요소를 수정), 원본 이미지와 다운 샘플링된 3개의 이미지를 하나의 데이터 세트로 결합함으로써 구성되었다.
투영 지오메트리의 특성으로 인해, 이는 카메라까지의 거리가 2, 4, 8의 스케일 팩터에 의해 증가된 원래 데이터 세트를 다시 렌더링하는 것과 유사하다.
이 데이터 세트에서 mip-NeRF를 학습할 때, 우리는 몇 개의 저해상도 픽셀이 많은 고해상도 픽셀과 비슷한 영향을 미치도록 원래 이미지에서 해당 픽셀의 풋프린트 면적만큼 각 픽셀의 손실을 스케일링한다(1/4 이미지에서 픽셀의 손실은 16 등).
이 작업의 평균 오류 메트릭은 네 가지 척도에 걸쳐 각 오류 메트릭의 산술 평균을 사용합니다.

이 다중 스케일 데이터 세트에 대한 mip-NeRF의 성능은 표 1에서 확인할 수 있다.
NeRF는 Blender 데이터 세트(표 2에 표시)의 SOTA이기 때문에, 우리는 NeRF와 몇 가지 개선된 버전의 NeRF만을 비교 평가합니다: "영역 손실"은 앞서 언급한 손실 함수의 크기를 mip-NeRF가 사용하는 픽셀 영역별로 추가하며, "중심 픽셀"은 각 픽셀 (Mildenhall et al.에서 수행한 것과 같이 각 픽셀의 모서리와 반대)의 중심을 통과하도록 각 ray의 방향에 추가된 반 픽셀 오프셋을 추가하며, "Misc"는 학습의 안정성을 약간 향상시키는 약간의 작은 변화를 추가한다(보충 참조).
우리는 또한 mip-NeRF의 몇 가지 ablations(mip-NeRF)에 대해 평가한다: "w/o Misc"은 이러한 작은 변화를 제거하고, "w/o single MLP"은 식 4의 NeRF의 2-MLP 학습 체계를 사용하며, "w/o Area Loss"은 픽셀 영역별 손실 스케일링을 제거하며, "w/o IPE"는 IPE 대신 PE를 사용하므로 mip-NeRF는 원뿔 캐스팅 대신 NeRF의 ray 캐스팅(중심 픽셀 포함)을 사용한다.
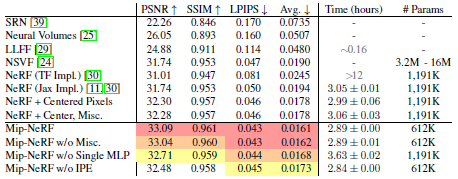
Mip-NeRF는 이 작업에서 평균 오류를 60% 줄이고 모든 메트릭과 규모에서 NeRF를 큰 폭으로 능가한다.
"중심" 픽셀은 NeRF의 성능을 크게 향상시키지만 mip-NeRF에 접근하기에는 충분하지 않다.
IPE 피쳐를 제거하면 mip-NeRF의 성능이 "중심" NeRF의 성능으로 저하되어 원뿔 캐스팅과 IPE 피쳐가 성능을 주도하는 주요 요인임을 입증한다.
"Single MLP" mip-NeRF ablation는 잘 수행되지만 매개 변수가 2배 더 많고 mip-NeRF보다 거의 20% 느리다(이 ablation은 t 값을 정렬해야 하는 필요성과 "coarse" 및 "fine" 척도에 걸쳐 변화하는 텐서 하드웨어 처리량이 낮기 때문일 수 있다).
또한 Mip-NeRF는 NeRF보다 약 7% 더 빠릅니다.
시각화는 그림 9 및 부록을 참조하십시오.
Blender Dataset
mip-NeRF가 수정하도록 설계된 샘플링 문제는 멀티 스케일 Blender 데이터 세트에서 가장 두드러지지만, mip-NeRF는 또한 표 2에 표시된 것처럼 Mildenhall et al. [30]에 제시된 쉬운 단일 스케일 Blender 데이터 세트에서 NeRF를 능가한다.
우리는 NeRF, NSVF [24]에서 사용한 베이스라인과 이전에 사용한 것과 동일한 변형과 ablation (mip-NeRF에서 이 작업에 사용하지 않는 "Area Loss" 제외)를 기준으로 평가한다.
mip-NeRF는 멀티스케일 Blender 데이터 세트보다 덜 눈에 띄지만 NeRF에 비해 평균 오류를 ~17% 줄이는 동시에 더 빠르다.
이러한 성능 향상은 그림 6과 같이 소형 또는 얇은 구조물과 같은 어려운 경우에 시각적으로 가장 뚜렷합니다.

Supersampling
서론에서 논의한 바와 같이, mip-NeRF는 안티 앨리어싱을 위한 사전 필터링 접근법이다.
대안적인 접근법은 슈퍼샘플링으로, 픽셀당 여러 개의 지터를 가진 ray를 캐스팅하여 NeRF에서 달성할 수 있다.
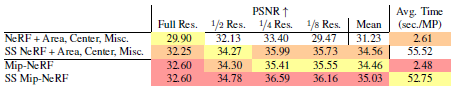
다중 스케일 데이터 세트는 전체 해상도 이미지의 다운샘플링 버전으로 구성되기 때문에, 우리는 전체 해상도 이미지만을 사용하여 NeRF("NeRF + Area, Center, Misc." 변형)를 학습시킨 다음 전체 해상도 이미지만 렌더링하여 "슈퍼샘플링된 NeRF"를 구성할 수 있다.
이 베이스라인은 불공평한 이점을 가지고 있다.
우리는 멀티 스케일 데이터 세트에서 저해상도 이미지를 수동으로 제거하며, 그렇지 않으면 이전에 입증되었듯이 NeRF의 성능이 저하될 수 있다.
이 전략은 대부분의 실제 데이터 세트에서 실행 가능하지 않다.
일반적으로 어떤 이미지가 이미지 콘텐츠의 규모에 해당하는지 a-priori를 알 수 없기 때문이다.
이 베이스라인의 장점에도 불구하고 mip-NeRF는 정확도와 일치하면서도 최대 22배 더 빠르다(표 3 참조).
5. Conclusion
NeRF 고유의 앨리어싱을 다루는 멀티스케일 NeRF 유사 모델인 mip-NeRF를 제시했습니다.
NeRF는 ray를 캐스팅하고, ray를 따라 점의 위치를 부호화하며, 별개의 척도로 개별 신경망을 학습시키는 방식으로 작동합니다.
반면 mip-NeRF는 원뿔을 캐스팅하고 원뿔형 frustum의 위치와 크기를 부호화하며 장면을 여러 척도로 모델링하는 단일 신경망을 학습시킵니다.
mip-NeRF는 샘플링 및 확장에 대해 명확하게 추론함으로써 자체 멀티스케일 데이터셋에서 NeRF에 대한 오류율을 60%, NeRF의 싱글스케일 데이터셋에서 17% 줄일 수 있으며, 동시에 NeRF보다 7% 더 빠릅니다.
또한 Mip-NeRF는 22배 더 빠르면서도 브루트포스 슈퍼샘플링된 NeRF 변종과 같은 정확성을 유지할 수 있습니다.
우리는 여기에 제시된 일반적인 기술이 ray 트레이싱 기반의 신경 렌더링 모델의 성능을 개선하기 위해 노력하는 다른 연구자들에게 유용하기를 바란다.
A. Conical Frustum Integral Derivations
원뿔형 frustum에 대한 uniform 분포의 다양한 모멘트에 대한 공식을 도출하기 위해, 우리는 (x, y, z) = φ(r, t, θ) = (rt cosθ, rt sinθ, t) for θ ∈ [0, 2π), t ≥ 0, |r| ≤ r˙로 매개 변수화된 축-정렬된 원뿔을 고려한다.
데카르트 공간으로부터의 이러한 변수 변화는 우리에게 미분 항을 제공한다:
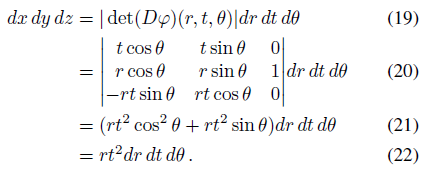
(균일 분포에 대한 정규화 상수 역할을 하는) 원뿔형 frustum의 부피는
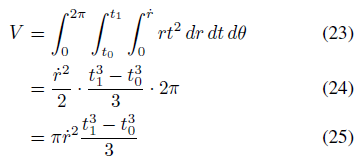
따라서 원뿔형 frustum에서 균일하게 샘플링된 점의 확률 밀도 함수는 rt^2 / V이다.
t의 첫 번째 모멘트는
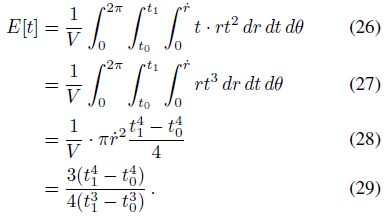
x와 y의 모멘트는 대칭에 의해 모두 0이다.
t의 두 번째 모멘트는
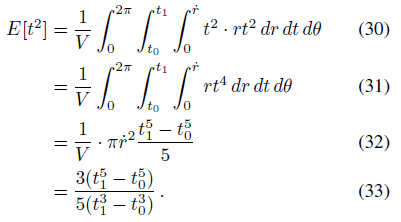
그리고 x의 두 번째 모멘트는
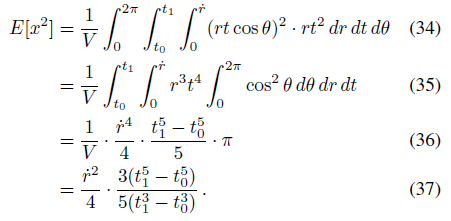
이다.
y의 두 번째 모멘트는 대칭에 의해 동일하다.
공분산의 모든 교차 항은 대칭에 의해 z입니다.
이러한 모멘트를 정의하면 원뿔형 frustum 내의 임의의 점에 대한 평균과 공분산을 구성할 수 있다.
ray 방향 μ_t를 따른 평균은 단순히 t에 대한 첫 번째 모멘트이다:
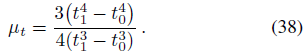
t에 대한 원뿔형 frustum의 분산은 분산의 정의에서 Var(t) = E[t^2] - E[t]^2를 따른다:
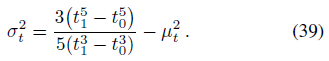
반지름 r에 대한 원뿔형 frustum의 분산은 x 또는 (대칭에 의한) y에 대한 frustum의 분산과 같다.
x에 대한 첫 번째 모멘트는 0이므로, 분산은 두 번째 모멘트와 같습니다:
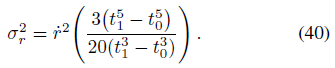
이 세 가지 양을 모두 주어진 형태로 계산하는 것은 수치적으로 불안정하다 — 큰 전력에 대해 제기되는 t_1과 t_0의 차이의 비율은 t_0과 t_1이 서로 가까이 있을 때 정확하게 계산하기 어려우며, 이는 학습 중에 자주 발생한다.
이러한 양을 실제로 사용하면 정확한 값 대신 0 또는 NaN이 생성되어 학습이 실패하는 경우가 많다.
따라서 우리는 이러한 방정식을 t_0과 t_1의 중심과 확산의 함수로 재매개한다: t_μ = (t_0 + t_1)/2이고, t_δ = (t_1 - t_0)/2입니다.
이를 통해 각 평균과 분산을 1차 항으로 다시 작성할 수 있으며, 이 항은 t_δ로 스케일링된 고차 항에 의해 수정됩니다.
이는 t_δ가 작을 때에도 안정적이고 정확한 값을 제공한다.
우리의 재측정된 값은

원뿔형 frustum의 기저와 상단 반경 사이에 상당한 차이가 있을 경우 원뿔형 frustum의 다변량 가우스 근사치가 부정확할 수 있으며, 이는 카메라 FOV가 클 때 카메라의 투영 중심 근처에 있는 frustum에 해당될 수 있다.
이것은 대부분의 데이터 세트에서 매우 드물지만, fisheye 렌즈를 사용한 매크로 촬영과 같은 비정상적인 상황에서 mip-NeRF를 사용하는 경우 문제가 될 수 있다.
B. The L Hyperparameter in PE and IPE
IPE 피쳐는 PE 피쳐의 일반화로 볼 수 있습니다: γ(x) = γ(μ = x, ∑ = 0).
또는 더 엄격하게, PE 피쳐들은 L 초 매개 변수에 의해 휴리스틱하게 결정되는 동일한 등방성 공분산 행렬을 갖는 모든 점들을 가정하는 "하드" IPE 피쳐들로 생각할 수 있다: L 값은 IPE에서 가우스 분산 함수가 IPE 피쳐의 "부드러운" 잘라내는 역할을 하는 것처럼 PE 피쳐가 잘리는 빈도를 결정합니다.
IPE 피쳐의 "부드러운" 최대 주파수는 전적으로 카메라의 기하학적 구조와 내재적 특성에 의해 결정되기 때문에 IPE 피쳐는 L 하이퍼 파라미터에 의존하지 않으므로 IPE 피쳐를 사용하면 L을 조정할 필요가 없다.
이는 PE에서 L 매개 변수는 PE의 고주파수가 잘리는 위치를 결정하지만, IPE에서는 이러한 고주파수가 인코딩에 대한 입력으로 사용되는 다변량 가우스의 크기에 의해 자연스럽게 감쇠되기 때문이다: 가우스가 작을수록 더 많은 고주파수가 유지됩니다.
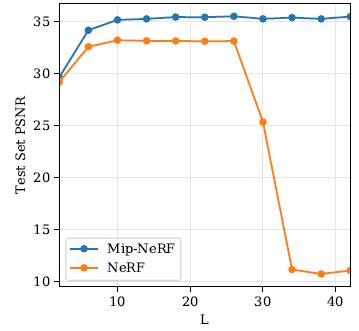
이를 입증하기 위해, 우리는 Mip-NeRF와 NeRF 모두에서 L의 "스위프"로 수행했고, 그림 7에 시각화된 단일 장면에 대해 테스트 세트 PSNR을 보고했습니다.
NeRF에서 성능을 최대화하는 L에 대한 값의 범위가 있지만 너무 크거나 너무 작은 값은 성능을 해친다는 것을 알 수 있습니다.
그러나 mip-NeRF에서 L은 임의로 큰 값으로 설정될 수 있고 성능은 영향을 받지 않는다는 것을 알 수 있다.
실제로, 우리는 논문의 모든 mip-NeRF 실험에서 L = 16으로 설정했는데, 이는 학습 중에 구성된 모든 IPE 피쳐의 마지막 차원이 수치 엡실론보다 작다는 결과를 낳는다.
C. Hyperparameters
본 논문의 모든 실험에서 우리는 Mildenhall et al. [30]에서 사용된 것과 정확히 동일한 초 매개 변수 세트를 사용하여 원뿔-캐스팅 및 IPE 피쳐와 관련된 mip-NeRF의 특정 기여를 격리하도록 주의를 기울인다.
mip-NeRF의 동작을 제어하는 세 가지 관련 초 매개 변수는 다음과 같다: 1) 두 레벨 각각에서 추출한 표본 N의 수(N = 128), 2) 미세 t 값(α = 0.01)을 샘플링하는 데 사용되는 coarse 투과율 가중치에 대한 히스토그램 "hyper parameter α", 그리고 3) 손실 함수의 "coarse" 성분에 대한 승수 λ. (λ = 0.1).
mip-NeRF는 이 세 가지 하이퍼 파라미터를 추가하지만 더 이상 사용되지 않는 세 가지 NeRF 하이퍼 파라미터도 사용하지 않습니다: 1) "coarse" MLP에 대해 추출한 샘플 N_c의 수(N_c = 64), 2) "fine" MLP에 대해 그려진 샘플 N_f의 수(N_f = 128), 3) 공간 위치 부호화에 사용되는 L도(L = 10).
mip-NeRF에서 사용되는 α 매개 변수는 NeRF에서 N_c와 N_f 사이의 균형과 유사한 목적을 수행한다.
N_c의 값이 클수록 최종 샘플(일정한 coarse 샘플과 편향된 fine 샘플의 정렬 조합)이 uniform 분포를 향해 편향되는 것처럼, α의 값이 클수록 렌더링 중에 사용되는 최종 샘플이 uniform 분포를 향해 편향된다.
Mip-NeRF의 곱셈기 λ는 NeRF에 아날로그가 없다, 왜냐하면 NeRF가 두 개의 다른 MLP를 사용한다는 것은 NeRF에서 "coarse" 손실과 "fine" 손실의 균형을 맞출 필요가 없다는 것을 의미하기 때문이다 - 고맙게도, mip-NeRF는 이 새로운 하이퍼 파라미터 λ를 튜닝할 필요성을 추가하지만, 동시에 섹션 B에서 논의한 L 하이퍼 파라미터를 튜닝할 필요성을 제거하므로 튜닝이 필요한 하이퍼 파라미터의 총 수는 두 모델 전체에서 일정하게 유지됩니다.
논문에서 실험을 실행하기 전에, 우리는 lego 장면의 검증 세트에서 α 및 λ 초 매개 변수를 손으로 간략하게 조정했다.
N은 튜닝되지 않았으며, mip-NeRF가 사용한 MLP 평가의 총 수가 NeRF가 사용한 총 수와 일치하도록 128로 설정되었다.
D. Forward-Facing Scenes
이 논문은 "Forward-Facing" 핸드헬드 휴대폰 카메라에 포착된 장면으로 구성된 LLFF 데이터 세트[29]를 평가하지 않는다는 점에 유의한다.
이러한 장면에서 NeRF는 "normalized device coordinates"(NDC) 공간에서 모델을 학습하고 평가했다.
NDC 좌표는 frustum-모양의 공간을 단위 큐브로 비선형적으로 뒤틀어 작업하며, 이는 다른 어려운 설계 결정(위치 인코딩을 사용하여 무한 3D 공간을 어떻게 표현해야 하는지)을 회피한다.
NDC 좌표는 이러한 "forward-facing" 장면에만 사용될 수 있으며, 카메라가 크게 회전하는 장면(대부분의 3D 데이터 세트의 경우)에서 NeRF는 기존의 3D "world 좌표"를 사용한다.
NDC 공간의 한 가지 흥미로운 결과는 픽셀에 해당하는 3D 볼륨이 frustum이 아니라 직사각형이라는 것이다 - NDC에서 xy 평면에 있는 픽셀의 공간적 지지는 기존의 투영 기하학에서와 같이 이미지 평면에서 거리에 따라 증가하지 않는다.
우리는 원뿔 대신 실린더를 캐스팅하여 NDC 공간에서 작동하는 mip-NeRF의 변형을 간략하게 실험했다.
이 작업에서 JaxNeRF가 달성한 평균 PSNR은 26.843이며, 이 실린더-캐스팅 변형 Mip-NeRF는 평균 PSNR 26.838을 달성합니다.
이 mip-NeRF 변형이 NeRF의 정확도와 대략 일치하기 때문에, 위치 인코딩에서 L 매개 변수를 조정할 필요가 없는 것으로 보인다.
이 결과는 NeRF가 전향적인 장면에서 잘 작동하는 이유에 대한 통찰력을 제공한다: NDC 공간에서는 캐스팅 ray에 대한 NeRF의 "잘못된" 앨리어스 접근법과 L 초 매개 변수 조정(섹션 B에서 논의한 바와 같이 등방성 가우시안과의 IPE 피쳐를 사용하는 것과 대략 동일)과 mip-NeRF의 더 "올바른" 앨리어스 방지 접근법 사이에 차이가 거의 없다.
본질적으로, NDC 공간에서 NeRF의 앨리어스 모델이 이미 mip-NeRF의 접근 방식과 매우 유사하기 때문에 NeRF는 이미 NDC 공간에서 원뿔 캐스팅 및 IPE 피쳐에 의해 제공되는 대부분의 이점을 얻을 수 있다.
장면 매개 변수화와 안티앨리어싱 사이의 이러한 상호 작용은 신경 렌더링 문제에서 좌표 공간의 신호 처리 분석이 추가적인 예상치 못한 이점 또는 통찰력을 제공할 수 있음을 시사한다.
E. Model Details
이 논문의 주요 기여는 원뿔 트레이싱, 통합 위치 인코딩 피쳐 및 단일 통합 멀티스케일 모델(NeRF의 별도 스케일 모델과는 대조적으로)의 사용인데, 이를 함께 사용하면 mip-NeRF가 멀티스케일 데이터를 더 잘 처리하고 앨리어싱을 줄일 수 있다.
또한, mip-NeRF는 mip-NeRF의 정확도 또는 속도를 의미 있게 변경하지 않지만, 우리의 방법을 약간 단순화하고 최적화 중에 견고성을 높이는 적은 수의 변경을 포함한다.
메인 논문의 "w/o Misc." ablations에 의해 언급된 이러한 "miscellaneous" 변화는 mip-NeRF의 성능에 크게 영향을 미치지 않지만, 향후 연구에서 유용하다는 것을 알 수 있기를 바라며 재현성을 위해 여기에 완전히 설명되어 있다.
E.1. Identity Concatenation
원래의 NeRF 논문에서, MLP에 대한 입력은 위치 및 뷰 방향의 위치 인코딩일 뿐만 아니라, 위치 인코딩과 위치 및 뷰 방향이 인코딩되는 연결이다.
우리는 이 "identity" 인코딩이 성능이나 속도에 의미 있게 기여하지 않는다는 것을 발견했고, 그것의 존재로 인해 IPE 피쳐의 공식화가 다소 어려워지기 때문에 mip-NeRF에서 이 identity 매핑은 제거되고 MLP에 대한 유일한 입력은 통합 위치 인코딩 자체이다.
E.2. Activation Functions
원래의 NeRF 논문에서, MLP가 예측 밀도 τ와 색상 c를 구성하기 위해 사용하는 활성화 함수는 각각 ReLU와 시그모이드이다.
τ를 생성하기 위한 활성화 함수로 ReLU를 사용하는 대신, 우리는 시프트된 softplus를 사용한다: log(1 + exp(x - 1)).
우리는 Softplus를 사용하면 MLP가 모든 곳에서 음의 값을 방출하는 재앙적인 고장 모드에 덜 취약한 더 부드러운 최적화 문제가 발생한다는 것을 발견했다(이 경우 τ의 모든 그레디언트가 0이고 최적화가 실패할 것이다).
softplus 내에서 -1에 의한 시프트는 mip-NeRF에서 τ를 생성하는 바이어스를 -1로 초기화하는 것과 동일하며, 이는 초기 τ 값을 작게 만든다.
NeRF의 밀도를 작은 값으로 초기화하면 조밀한 장면 콘텐츠가 "뒤에" 있는 장면 콘텐츠의 그레디언트를 억제하기 때문에 학습 시작 시 약간 더 빠른 최적화가 이루어진다.
색 c를 생성하기 위한 시그모이드 대신, 우리는 [0, 1](입력 RGB 강도의 범위)의 약간 바깥에 포화시키는 "넓어진" 시그모드를 사용한다: (1 + 2ε)/(1 + exp(-x)) - ε, ε = 0.001
이는 학습이 그레디언트가 0인 시그모이드 꼬리에 네트워크 활성화를 포화시켜 검은색 또는 흰색 픽셀을 설명하려고 시도하는 드문 실패 모드를 방지하여 최적화가 실패할 수 있다.
네트워크가 입력 값 범위를 약간 벗어난 값으로 포화되도록 함으로써 활성화가 포화되도록 권장되지 않습니다.
활성화 함수에 대한 이러한 변경은 성능에 거의 영향을 미치지 않지만, 큰 학습률을 사용할 때 학습 안정성을 향상시킨다는 것을 발견했다(본 논문의 모든 결과는 공정한 비교를 위해 Mildenhall et al. [30]에서 사용한 것과 동일한 낮은 학습률을 사용함).
E.3. Optimization