2022. 2. 23. 17:59ㆍView Synthesis
NeRF++: Analyzing and Improving Neural Radiance Fields
Kai Zhang, Gernot Riegler, Noah Snavely, Vladlen Koltun
Abstract
Neural Radiance Fields(NeRF)는 경계 장면의 360˚ 캡처와 경계 및 경계 없는 장면의 정향 캡처를 포함한 다양한 캡처 설정에 대해 인상적인 view synthesis 결과를 달성한다.
NeRF는 뷰 불변도 및 뷰 의존적 컬러 볼륨을 나타내는 다층 퍼셉트론(MLP)을 훈련 이미지 세트에 맞추고 볼륨 렌더링 기술을 기반으로 새로운 뷰를 샘플링한다.
이 기술 보고서에서는 먼저 광도 장과 그 잠재적 모호성, 즉 형상 방사 모호성에 대해 언급하고, 그러한 모호성을 피하는 NeRF의 성공을 분석한다.
둘째, 우리는 대규모 무한 3D 장면 내에서 개체의 360˚ 캡처에 NeRF를 적용하는 것과 관련된 매개 변수화 문제를 다룬다.
우리의 방법은 이 어려운 시나리오에서 view synthesis 충실도를 향상시킨다.
1. Introduction
당신이 가장 좋아하는 장소의 사진 몇 장을 캡처했던 지난 휴가를 떠올려보세요.
이제 집에서 여러분은 이 특별한 장소를 가상으로라도 다시 걸어 다니고 싶어할 것입니다.
이렇게 하려면 무한 장면에서 서로 다른 자유롭게 배치된 뷰포인트에서 동일한 장면을 렌더링해야 합니다.
이 novel view synthesis 과제는 컴퓨터 비전과 그래픽의 오랜 문제이다(Chen & Williams, 1993; Devevec 등, 1996; Levoy & Hanrahan, 1996; Gortler 등, 1996; Shum & Kang, 2000).
최근 학습 기반 방법은 사진 현실적 novel view synthesis를 향한 상당한 진전으로 이어졌다.
특히 Neural Radiance Fields(NeRF)의 방법이 상당한 관심을 끌었다(Mildenhall 등, 2020).
NeRF는 5D 벡터(3D 좌표와 2D 보기 방향)를 불투명도 및 색상 값에 매핑하는 암시적 MLP 기반 모델로, 모델을 학습용 뷰 집합에 적합시켜 계산합니다.
그런 다음 결과 5D 기능을 사용하여 기존의 볼륨 렌더링 기술로 새로운 뷰를 생성할 수 있다.
이 기술 보고서에서는 먼저 NeRF의 잠재적 고장 모드에 대한 분석과 NeRF가 실제로 이러한 고장 모드를 피하는 이유에 대한 분석을 제시한다.
둘째, NeRF가 무한 장면의 새로운 종류의 캡처에서 작업할 수 있도록 하는 inverted sphere parameterization이라고 하는 새로운 공간 매개 변수화 체계를 제시한다.

특히, 이론적으로 훈련 이미지 세트에서 5D 기능을 최적화하면 정규화가 없는 경우 새로운 테스트 뷰로 일반화하지 못하는 중요한 퇴화 솔루션에 직면할 수 있다.
이러한 현상은 shape-radiance ambiguity(그림 1, 왼쪽)으로 캡슐화되며, 여기서 각 표면 지점에서 발신 2D 방사도를 적절하게 선택하여 임의의 잘못된 형상에 대해 훈련 이미지 세트를 완벽하게 맞출 수 있다.
우리는 NeRF에 사용되는 특정 MLP 구조가 그러한 모호성을 피하는 데 중요한 역할을 하여 새로운 관점을 합성할 수 있는 인상적인 능력을 제공한다는 것을 경험적으로 보여준다.
우리의 분석은 NeRF의 인상적인 성공에 대한 새로운 관점을 제공한다.
우리는 또한 무한 환경 내의 물체 주변의 360˚ 캡처와 관련된 도전적인 시나리오에서 발생하는 공간 매개 변수화 문제를 다룬다(그림 1, 오른쪽).
360˚ 캡처의 경우 NeRF는 전체 장면이 경계 볼륨으로 채워질 수 있다고 가정하며, 이는 대규모 장면에서 문제가 된다: 장면의 작은 부분을 볼륨에 맞추고 상세하게 샘플링하지만 배경 요소를 완전히 캡처하는 데 실패한다; 또는 샘플링 해상도가 제한되어 있기 때문에 전체 장면을 볼륨에 맞추고 모든 부분에서 세부 정보가 부족합니다.
우리는 반전 구면 장면 매개 변수화로 무한 3D 배경 콘텐츠를 모델링하는 과제를 해결하면서 전경과 배경을 별도로 모델링하는 단순하면서도 효과적인 솔루션을 제안한다.
Tanks and Temples 데이터 세트(Knapitsch 등, 2017)와 라이트 필드 데이터 세트(Yöucer 등, 2016)로부터 실제 캡처에 대한 개선된 양적 및 질적 결과를 보여준다.
요약하면, 우리는 NeRF가 shape-radiance 모호성을 해결하기 위해 관리하는 방법에 대한 분석과 360˚ 캡처의 경우 무한 장면의 매개 변수화에 대한 해결책을 제시한다.
2. Preliminaries
정적 장면의 포즈된 다중 뷰 영상이 주어지면 NeRF는 뷰 의존적인 표면 질감을 나타내는 광도 필드 c와 함께 부드러운 모양을 나타내는 불투명도 필드 σ를 재구성합니다.
σ와 c 모두 다층 퍼셉트론(MLP)으로 암시적으로 표현된다.
불투명도 필드는 3D 위치 x ∈ R^3의 함수로 계산되며, 광도 필드는 3D 위치 및 보기 방향 d ∈ S^2(즉, 단위 3-벡터 세트)에 의해 파라미터화된다.
따라서, 우리는 불투명도를 위치의 함수로 나타낼 때 σ(x)를 사용하고, 광도를 위치와 보는 방향의 함수로 나타낼 때 c(x, d)를 사용한다.
이상적으로, σ는 불투명 재료에 대한 ground-truth 표면 위치에서 정점을 찍어야 하며, 이 경우 c는 표면 광장으로 감소한다(Wood 등, 2000).
n개의 훈련 영상이 주어졌을 때 NeRF는 확률적 경사 강하를 사용하여 ground-truth 관측 이미지 I_i와 동일한 시야에서 렌더링된 예측 이미지 ^I_i(σ, c) 사이의 불일치를 최소화함으로써 최적화 σ 및 c를 사용한다.

암묵적 볼륨 σ와 c는 ^I(σ, c)의 각 픽셀을 렌더링하기 위해 광선 추적된다(Kajya & Von Herzen, 1984).
주어진 선 r = o + td, o ∈ R^3, d ∈ S^2, t ∈ R^+의 경우, 그것의 색은 적분

에 의해 결정된다.
네트워크의 스펙트럼 편향을 보상하고 더 선명한 이미지를 합성하기 위해 NeRF는 x와 d를 푸리에 특징에 매핑하는 위치 인코딩 γ를 사용한다(Tancik 등, 2020):

여기서 k는 푸리에 형상 벡터의 치수를 지정하는 초 매개 변수이다.
3. Shape-radiance Ambiguity
뷰 의존적인 외관을 모델링하는 NeRF의 능력은 정규화가 없을 때 퇴화된 솔루션을 인정할 수 있는 3D 모양과 광도 사이의 내재적인 모호성으로 이어진다.
임의의 부정확한 모양의 경우, 학습 이미지를 완벽하게 설명하는 광도장 패밀리가 존재하지만 새로운 테스트 뷰로 일반화되지 않는다는 것을 보여줄 수 있다.
이러한 모호성을 설명하기 위해 주어진 장면에서 우리가 기하학을 단위 구로서 나타낸다고 상상해보자.
즉, NeRF의 불투명도 필드를 단위구 표면에 1로 고정하고, 그 외의 경우에는 0으로 고정하자.
그런 다음 각 훈련 이미지의 각 픽셀에 대해 해당 픽셀을 통과하는 광선을 구와 교차하고 교차점(및 광선 방향을 따라)의 광도 값을 해당 픽셀의 색이 되도록 정의한다.
이 인위적으로 구성된 솔루션은 입력 이미지에 완벽하게 맞는 유효한 NeRF 재구성이다.
그러나 새로운 관점을 합성하는 이 솔루션의 기능은 매우 제한적이다.
그러한 관점을 정확하게 생성하는 것은 각 표면 지점에서 임의의 복잡한 뷰 의존적 함수를 재구성하는 것을 포함할 것이다.
이 모델은 기존의 라이트 필드 렌더링 작업처럼 훈련 뷰가 매우 조밀하지 않는 한 그러한 복잡한 함수를 정확하게 보간할 가능성이 매우 낮다(Buehler 등, 2001; Levoy & Hanrahan, 1996; Gortler 등, 1996).
이러한 형태-방사선 모호성은 그림 2에 설명되어 있습니다.
NeRF가 이러한 퇴화된 솔루션을 피하는 이유는 무엇입니까?
우리는 NeRF의 구조에 두 가지 관련 요인이 온다고 가정한다:
1) 잘못된 지오메트리는 대조적인 동안 방사장이 더 높은 고유 복잡성(즉, 훨씬 더 높은 주파수)을 갖도록 강제한다.
2) NeRF의 특정 MLP 구조는 표면 반사율에 앞서 매끄러운 BRDF를 암시적으로 인코딩한다.
Factor 1:
σ가 정확한 모양에서 벗어나므로, 입력 영상을 재구성하려면 일반적으로 c는 d와 관련하여 고주파 함수가 되어야 합니다.
정확한 형상의 경우 light field은 일반적으로 훨씬 더 부드러울 것이다(사실 램버트 재료의 경우 상수).
부정확한 형상에 필요한 높은 복잡도는 제한된 용량 MLP로 표현하기가 더 어렵습니다.

Factor 2:
특히, NeRF의 특정 MLP 구조는 주어진 표면 지점 x에서 d에 대해 c가 매끄러운 평활 표면 반사 함수를 선호하는 암묵적인 선행 기능을 암호화한다.
그림 3에 표시된 이 MLP 구조는 장면 위치 x와 시야 방향 d를 비대칭적으로 처리한다, d는 MLP의 끝에 가까운 네트워크에 주입된다, 즉, 뷰 의존적 효과의 생성에 관여하는 MLP 매개변수가 적을 뿐만 아니라 비선형 활성화도 적다는 것을 의미한다.
또한, 보기 방향을 인코딩하는 데 사용되는 푸리에 기능은 저주파 성분으로만 구성된다.
즉, d 대 x 인코딩을 위한 γ^4(·) 대 γ^10(·)이다(식 (3) 참조).
즉, 고정된 x의 경우, c(x, d)의 광도는 d에 대해 제한된 표현력을 가진다.

이 가설을 검증하기 위해, 우리는 대신 x와 d를 대칭적으로 처리하는 vanilla MLP로 c를 나타내는 실험을 수행한다,—즉, 첫 번째 계층에 대한 입력으로 두 가지를 모두 수용하고 γ^10(·)으로 인코딩하는 것—네트워크 구조에서 발생하는 방향 보기와 관련된 암시적 우선 순위를 제거합니다.
c에 대한 이 대체 모델을 사용하여 처음부터 NeRF를 학습하면 그림 4와 표 1에 표시된 바와 같이 NeRF의 특수 MLP에 비해 테스트 이미지 품질이 저하됩니다.
이 결과는 방사 c의 NeRF의 MLP 모델에서 반사율의 암묵적 정규화가 올바른 솔루션을 복구하는 데 도움이 된다는 우리의 가설과 일치한다.

4. Inverted Sphere Parametrization
식 (2)의 체적 렌더링 공식은 유클리드 깊이에 걸쳐 통합된다.
실제 장면 깊이의 동적 범위가 작을 때, 적분은 제한된 수의 샘플로 수치적으로 잘 근사될 수 있다.
그러나 주변 환경을 관찰하는 주변 물체를 중심으로 한 야외 360˚ 캡처의 경우 배경(건물, 산, 구름 등)이 임의로 멀리 떨어져 있을 수 있어 동적 깊이 범위가 매우 클 수 있다.
그러한 높은 동적 깊이 범위는 사실적인 광 이미지를 합성하기 위해 식 (2)의 적분은 전경과 배경 영역 모두에서 충분한 분해능이 필요하기 때문에 NeRF의 체적 장면 표현에 심각한 분해능 문제를 초래한다, 이는 3D 공간의 유클리드 매개 변수화에 따라 단순히 점을 샘플링하는 것으로 달성하기 어렵다.
그림 5는 장면 커버리지와 상세 캡처 사이의 이러한 균형을 보여준다.
모든 카메라가 장면 콘텐츠에서 카메라를 분리하는 평면을 향해 전진하는 보다 제한된 시나리오에서 NeRF는 유클리드 공간의 하위 집합을 투영적으로 매핑하여 이 해상도 문제를 해결한다, 즉, 레퍼런스 카메라의 시야가 답답한 경우 정규화된 장치 좌표(NDC)(McReynolds & Blythe, 2005)로 변환하고 이 NDC 공간에 통합한다.
그러나 이 NDC 매개 변수화는 또한 참조 뷰 절망을 벗어나는 공간을 포함하지 못하기 때문에 가능한 시점을 근본적으로 제한한다.

우리는 자유 보기 합성을 용이하게 하는 반전 구 매개 변수화로 이 제한을 해결한다.
우리의 표현에서, 우리는 먼저 장면 공간을 두 개의 볼륨, 즉 내부 볼륨의 보완을 포함하는 내부 단위 구체와 반전된 구에 의해 표현되는 외부 볼륨으로 분할한다(이 방식으로 모델링된 장면의 실제 예는 그림 6 참조).
내부 볼륨에는 전경과 모든 카메라가 포함되어 있는 반면 외부 볼륨에는 환경의 나머지 부분이 포함되어 있습니다.


이 두 볼륨은 두 개의 개별 NeRF로 모델링된다.
광선의 색을 렌더링하기 위해, 그것들은 개별적으로 레이캐스트되고, 그 다음에 최종 합성이 이루어진다.
장면의 해당 부분이 잘 제한되기 때문에 내부 NeRF에 대해 재매개변수가 필요하지 않다.
외부 NeRF에 대해, 우리는 반전된 구 파라미터화를 적용한다.
특히, 외부 볼륨에서 3D 포인트 (x, y, z), r = (x^2 + y^2 + z^2)^(1/2) > 1은 4중 (x', y', z', 1/r), x'^2 + y'^2 + z'^2 = 1로 재측정될 수 있습니다, 여기서 (x', y', z')는 (x, y, z)와 같은 방향의 단위 벡터이고, 0 < 1/r < 1은 구 바깥의 점 r · (x', y', z')를 지정하는 이 방향의 역반경이다.
물체가 원점에서 무제한으로 떨어져 있을 수 있는 유클리드 공간과는 달리, 재매개변수화된 4중접의 모든 숫자들은 경계로 묶여 있다, x', y', z' ∈ [-1, 1], 1/r ∈ [0, 1].
이렇게 하면 숫자 안정성이 향상될 뿐만 아니라 객체가 멀어질수록 해상도가 낮아집니다.
이 4D 경계 볼륨(자유도 3도)을 직접 레이캐스트하여 카메라 광선의 색상을 렌더링할 수 있습니다.
전경과 배경의 합은 식 (2)의 적분을 내부 볼륨과 외부 볼륨으로 통합하는 두 부분으로 나누는 것과 같습니다.
특히, 선 r = o + td가 단위구에 의해 두 개의 세그먼트로 분할된다고 가정하자: 첫 번째에서는 t ∈ (0, t')가 구 안에 있고, 두 번째에서는 t ∈ (t', ∞)가 구 외부에 있다.
우리는 방정식 2에 통합된 볼륨 렌더링을

로 다시 작성할 수 있다.
항 (i)와 (ii)는 유클리드 공간에서 계산되는 반면, 항 (iii)는 1/r을 적분 변수로 하여 반전구 공간에서 계산된다.
다시 말해, 우리는 (i)와 (ii)의 항으로 σ_in (o+td), c_in (o+td, d)을 사용하고, (iii)의 항으로 σ_out (x', y', z', z' 1/r), c_out (x', y', z' 1/r, d)를 사용한다.
광선 r = o + td에 대한 항 (iii)을 계산하기 위해서는 먼저 σ_out, c_out을 임의의 1/r에서 평가할 수 있어야 한다.
즉, 주어진 1/r에 해당하는 (x', y', z')를 계산하여 σ_out, c_out을 (x', y', z', 1/r) 입력으로 사용할 수 있는 방법이 필요합니다.
이 작업은 다음과 같이 수행할 수 있습니다.
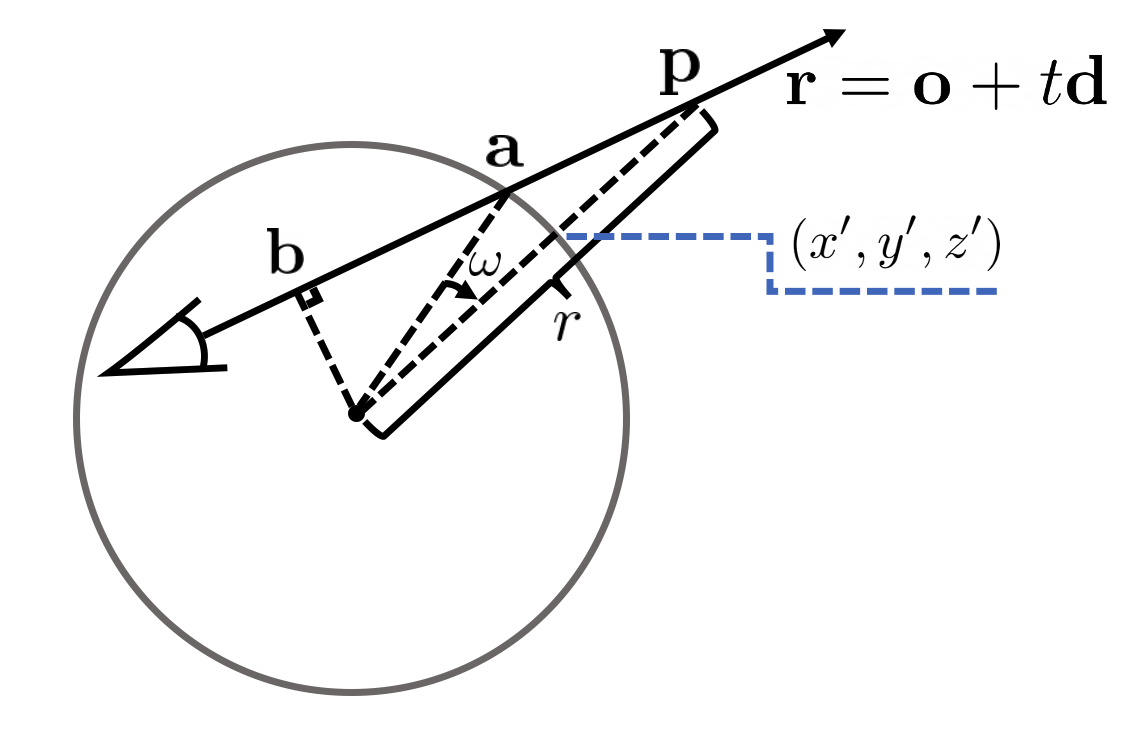
그림 8과 같이, 광선이 a 지점에서 단위구와 교차하게 하고, 광선과 정렬된 화음의 중간점이 b점이 되게 한다.
점 a = o + t_a d는 |o + t_a d| = 1을 풀어서 계산하는 반면, b = o + t-b d는 d^T (o + t_b d) = 0을 풀어서 얻는다.
(x', y', z')를 얻기 위해, 우리는 벡터 b x d를 따라 ω = arcsin |b| - arcsin(|b| · 1/r ) 각도로 벡터 a를 회전시킬 수 있다.
일단 우리가 σ_out, c_out을 임의의 1/r에서 평가할 수 있다면, 우리는 단지 [0, 1]부터 (iii)까지의 한정된 수의 점들을 샘플링한다.
외부 볼륨에 대한 반전 구 파라미터화는 직관적인 물리적 설명을 가지고 있습니다.
영상 평면이 장면 원점에서 단위구인 가상 카메라의 관점에서 볼 수 있다.
따라서 3D 포인트 (x, y, z)은 영상 평면의 픽셀(x', y', z')에 투영되는 반면 항 1/r ∈(0, 1)은 포인트의 (역) 깊이 또는 불균형으로 작용한다.
이러한 관점에서, 정향 캡처에만 적합한 NDC 매개 변수화는 구형 투영 표면이 아닌 가상 핀홀 카메라를 사용하기 때문에 우리의 표현과 관련이 있다.
이러한 의미에서, 우리의 반전된 구 매개 변수화는 뷰 합성에 대한 최근 연구(Attal et al., 2020; Broxton et al., 2020)에서 제안된 다중 구 이미지(구 중심에서 역 깊이에 따라 샘플링된 중첩된 동심원으로 구성된 장면 표현)의 개념과 관련이 있다.
5. Experiments
6. Open Challenges
NeRF++는 전경과 배경이 모두 광선학을 위해 충실하게 표현되어야 하는 무한 장면의 매개 변수화를 개선한다.
그러나 아직 해결되지 않은 과제가 많이 남아 있다.
첫째, 단일 대규모 장면에서 NeRF 및 NeRF++를 학습하고 테스트하는 것은 상당히 많은 시간과 메모리가 소요된다.
4개의 RTX 2080Ti GPU가 있는 노드에서 NeRF++를 학습하는 데 최대 24시간이 걸립니다.
이러한 GPU 하나에 1280x720 이미지 하나를 렌더링하는 것은 테스트 시간에 최대 30초가 걸립니다.
Liu et al. (2020)은 추론을 가속화했지만, 렌더링은 여전히 실시간과는 거리가 멀다.
둘째, 작은 카메라 보정 오류는 사실적 합성을 방해할 수 있습니다.
상황별 손실(Mechrez 등, 2018)과 같은 강력한 손실 함수를 적용할 수 있다.
셋째, 이미지 충실도를 높이기 위해 자동 노출 및 조명과 같은 광도 측정 효과도 고려할 수 있다.
이 조사 라인은 Martin-Brualla 등(2020)의 직교 작업에서 다루어진 조명 변화와 관련이 있다.