2022. 4. 28. 13:33ㆍView Synthesis
Stereo Radiance Fields (SRF): Learning View Synthesis for Sparse Views of Novel Scenes
Julian Chibane, Aayush Bansal, Verica Lazova, Gerard Pons-Moll
Abstract
최근의 신경 뷰 합성 방법은 다중 뷰 재구성에 의존하는 고전적인 파이프라인을 능가하는 인상적인 품질과 사실성을 달성했다.
NeRF[34]와 같은 SOTA 방법은 신경망으로 단일 장면을 학습하도록 설계되었으며 고밀도 멀티뷰 입력이 필요하다.
새로운 장면에서 테스트를 하려면 처음부터 다시 학습해야 하는데, 2-3일이 걸린다.
본 연구에서는 종단 간 학습을 받고, 새로운 장면으로 일반화하며, 테스트 시 희소 뷰만 요구하는 신경 뷰 합성 접근법인 Stereo Radience Fields (SRF)를 소개한다.
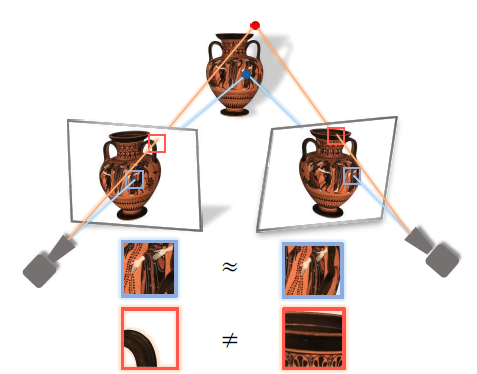
핵심 아이디어는 스테레오 이미지에서 유사한 이미지 영역을 찾아 표면 점을 추정하는 고전적인 다중 뷰 스테레오 방법에서 영감을 얻은 신경 아키텍처이다.
SRF에서는 입력 이미지에서 스테레오 대응 인코딩이 주어지면 각 3D 포인트에 대한 색과 밀도를 예측한다.
인코딩은 고전 스테레오 에뮬레이션과 같은 쌍별 유사성의 앙상블에 의해 암묵적으로 학습된다.
실험에 따르면 SRF는 장면에 오버핏하는 대신 구조를 학습한다.
우리는 DTU 데이터 세트의 여러 장면에서 학습하고 재학습 없이 새로운 장면으로 일반화하여 입력으로 10개의 희소 및 분산 뷰만 필요로 한다.
우리는 10-15분 간의 미세 조정이 결과를 더욱 개선하여 장면별 모델보다 훨씬 더 샤프하고 자세한 결과를 달성한다는 것을 보여준다.
1. Introduction

우리는 종단 간 학습을 받고, 새로운 장면으로 일반화되며, 테스트 시 희소 뷰만 필요한 신경 다중 뷰 합성 접근법을 도입한다(그림 1-(b)).
이는 특정 장면에 대해 학습되고 샤프한 결과를 내기 위해 고밀도 다중 뷰가 필요한 NeRF[34]와 같은 SOTA 뷰 합성 방법과 극명한 대조를 이룬다.

방법의 뷰 합성 스펙트럼의 한쪽 끝에는 인상적인 결과를 보여 준 NeRF[34]와 같은 순수한 데이터 중심 방법이 있다.
NeRF는 위치와 방향에서 방출된 radiance에 대한 매핑을 학습하여 급진적인 데이터 중심 접근 방식을 취한다.
이 매핑은 특정 장면에 대해 특별히 학습됩니다(그림 2-(a)).
새로운 장면으로 일반화하려면 2일 동안 재학습이 필요하며 희박하고 분산된 뷰에 대해 학습할 경우 결과가 블러하다(그림 1-(a)).
다른 한편으로, 널리 사용되는 고전적인 이미지 기반 렌더링 기법[46]은 기하학[8, 29, 44, 45]을 사용한다.
이러한 접근 방식은 대응[39, 41, 49] 또는 멀티뷰 3D 재구성[42, 43]을 통해 원하는 타겟 뷰로 픽셀을 왜곡합니다.
결과적으로, 이러한 방법은 고밀도 멀티 뷰가 필요한 고품질 3D 재구성 또는 고밀도 픽셀당 대응에 의존한다.
최근 연구[5, 38]는 고전적인 방법의 왜곡된 관점을 수정하는 방법을 학습하여 고전적인 방법과 데이터 기반 접근 방식을 결합한다.
이러한 방법[5, 38]의 순차적 파이프라인은 종단 간 학습을 허용하지 않는다.
우리는 고전적인 방법과 순수한 데이터 중심 방법 모두에서 영감을 얻는다.
NeRF와 마찬가지로, 우리는 또한 radiance(특히 색과 밀도)를 예측하기 위한 신경망을 배운다.
그러나 3D 위치에서 장면 radiance를 기억하는 대신 이미지 기반 피쳐 인코딩을 사용하여 네트워크가 장면 지오메트리에 대해 추론할 수 있다(그림 2-(b)).
고전 스테레오 재구성 [41, 49]에서, 뷰 간의 대응은 유사성 점수를 계산하여 찾을 수 있다.
우리는 명시적 대응을 계산하지 않고 고전적인 접근 방식을 모방하지만 종단 간 학습이 가능한 SRF(Steadio Radience Fields)라는 아키텍처를 고안한다.
3D 점이 각 사용 가능한 뷰에 투영되어 점별 뷰 피쳐를 추출합니다.
그런 다음 뷰 피쳐는 필터 뱅크에 의해 쌍으로 처리되며, 필터 뱅크는 고전적인 방법의 대응 결과를 에뮬레이트한다(그림 3).
쌍별 점수의 결과 매트릭스는 사용 가능한 뷰의 정보를 통합하여 해당 지점에서 원하는 radiance를 예측하는 컨볼루션 신경망[21]으로 추가로 처리된다.
우리의 실험은 아키텍처 내에 다중 뷰 재구성 아이디어를 통합하면 일반화 능력이 크게 향상된다는 것을 보여준다.
단일 장면에서 학습하고 새로운 장면에서 테스트할 때 SRF는 합리적인 결과를 생성할 수 있습니다.
이것은 네트워크가 장면을 기억하지 않고 구조에 대해 추론하는 방법을 배운다는 것을 나타낸다.
여러 장면(100개 이상)에 대해 학습할 때 SRF는 10개의 희소 및 분산 뷰만 입력으로 사용할 수 있는 경우에도 새로운 장면으로 일반화할 수 있다.
추가적인 개선은 10개의 뷰(그림 1-(c))를 미세 조정함으로써 얻을 수 있습니다(그림 1-(c)).
이는 일반적으로 처음부터 다시 학습하는 방법에 필요한 2-3일보다 훨씬 짧은 시간입니다[34, 47].
SRF 결과는 더 샤프해서 다중 뷰 재구성 구조가 일반화에 도움이 될 뿐만 아니라 학습 문제를 제한한다는 것을 검증한다.
우리는 독자들이 우리의 결과를 우리의 프로젝트 페이지에서 이용 가능한 비디오로 볼 것을 권장한다.
요약하면 우리의 기여는 다음과 같습니다:
• 우리는 다중 뷰 합성을 위한 종단 간 self-supervised 아키텍처인 Stereo Radiance Fields (SRF)를 소개한다.
우리는 고전적인 다중 뷰 재구성 파이프라인과 신경 렌더링 접근법의 통찰력을 수집한다.
• 실험은 SRF가 희소하고 분산된 뷰를 입력으로 제공하는 새로운 장면으로 일반화한다는 것을 보여준다.
또한 테스트 분포에서 몇 분 동안 사전 학습된 SRF를 미세 조정하면 결과가 향상된다.
• 우리는 최근의 패러다임을 하나의 모델로 결합하는 방법을 보여주는데, 이는 종종 새로운 관점 합성에서 고립적으로 처리된다.
SRF는 고전적인 다중 관점 3D 재구성과 여러 장면에서 학습을 기반으로 한다.
• 희소 및 분산 뷰 설정에서 SRF는 NeRF와 같은 SOTA 베이스라인보다 훨씬 더 샤프한 결과를 생성한다[34].
우리는 이틀 동안 10개의 테스트 뷰에서 학습된 NeRF와 달리 15분 동안만 미세 조정할 때 훨씬 더 나은 결과를 얻는다.
2. Multi-View View Synthesis
N개의 카메라 뷰를 고려할 때, 우리의 목표는 새로운 가상 카메라를 위한 뷰를 합성하는 것이다.
이것은 오랜 문제입니다 [17, 50].
역사적으로 [46], 이 문제는 사용된 기하학적 정보에 따라 세 가지 가능한 방향으로 연구되었다:
(1) 가능한 모든 각도에서 주어진 카메라에 대한 레이의 강도를 계산하기 위해 플레놉틱 함수를 모델링하여 기하학 없이 렌더링 [2, 16, 22, 30, 35];
(2) 다중 요소에 걸친 위치 대응에 대한 지식이 필요한 대응[8,44]을 사용한 렌더링;
그리고 (3) depth 또는 포인트 클라우드의 형태로 명시적인 3D 정보가 필요한 명시적 지오메트리 [29, 45]로 렌더링합니다.
이 작업에서, 우리는 신경 렌더링의 통찰력을 고전적인 재구성 파이프라인과 결합한다.
우리는 네트워크 내에서 쌍별 점수의 앙상블을 계산하여 네트워크가 뷰 쌍 간의 대응에 대해 추론하도록 권장한다.
우리는 결코 명시적으로 대응관계를 계산하지 않지만, 이러한 기하학적 추론은 우리가 새로운 장면으로 일반화할 수 있게 해준다.
Correspondences across multi-views:
멀티 뷰 스테레오의 고전적인 접근법[8, 13, 17, 44, 51]은 뷰 간의 대응에 의존한다.
이 연구에서, 우리는 고전적인 멀티 뷰 스테레오[17, 46]와 현대 학습 기반 접근법[10, 34, 40]의 통찰력을 결합한다.
우리는 10개의 멀티 뷰를 입력하고 멀티 스케일 피쳐를 추출하는 인코더 네트워크를 사용한다[4, 40].
우리는 고전적인 블록 또는 피처 매칭을 유사성 점수의 앙상블을 출력하는 다층 퍼셉트론(MLP)으로 대체한다.
우리와 마찬가지로, 최근 연구는 명시적 대응을 통합하는 희소 뷰[5]에서 뷰 합성을 할 수 있다.
그러나 명시적으로 대응물을 계산하는 것은 조도, 확대/축소, 규모 및 폐색의 차이로 인해 어렵다.
장면별 모델은 아티팩트를 수정하도록 학습된다.
우리의 방법에서, 네트워크는 뷰 합성 loss에 의해 주도되는 대응에 대한 이유이지만, 그것들은 절대 명시적으로 계산되지 않는다.
중요한 것은 우리 모델이 장면에 국한되지 않는다는 것이다.
Neural Rendering and Plenoptic Modeling:
SOTA 신경 렌더링[52] 접근 방식은 심층 신경망을 사용하여 사진 사실적인 시각적 콘텐츠를 만들 수 있게 했다[21].
다중 뷰 합성에는 세 가지 일반적인 방향이 있습니다:
(1) plane-sweep stereo [13, 15] 또는 multi-plane image (MPI) 표현 사용 [61].
MPI 기반 접근법[7, 14, 15, 20, 33, 48]은 작은 베이스라인 이동에 대한 연속적인 뷰 합성에서 주목할 만한 결과를 보여주었지만, 정확한 다중 평면 이미징을 가정하기 때문에 대규모의 경우에는 실패했다.
(2) 뷰 합성을 위해 SfM[42, 43] 또는 멀티 뷰 스테레오[19]를 사용하여 명시적으로 통합했다.
이러한 접근 방식은 뷰 합성을 위해 신경망과 함께 사용되는 상당히 밀도가 높은 3D 포인트 클라우드를 가정한다.
신경망의 역할은 3D 재구성의 결함을 수정하는 것이다.
그러나 이러한 접근 방식은 명시적 3D 재구성이 실패하기 때문에 뷰가 희소하고 작은 중첩이 있을 때 어려움을 겪는다.
그리고 (3) 최근의 접근 방식[23, 24, 27, 34, 37, 47, 57, 58]은 새로운 뷰를 합성하기 위해 미분 가능한 ray marching 작업과 결합할 수 있는 3D 표현을 학습한다.
설계에 의한 이러한 접근 방식에는 장면별 모델링이 필요하다.
이것은 (1) 모델을 학습하는 데 2 - 3일이 필요하기 때문에 새로운 캡처의 즉각적이고 온라인 시각화를 제한한다; (2) 인식, semantic segmentation 및 탐지와 같은 다른 시각 영역의 발전을 위한 원동력이 된 대량의 다양한 시각 데이터를 활용한다.
우리의 연구는 최근의 신경 렌더링 접근법에서 깊은 영감을 받았다.
NeRF[34]와 마찬가지로 연속적인 위치에서 radiance를 예측하고 볼륨 렌더링을 사용하여 타겟 이미지를 생성한다.
포인트 좌표와 radiance를 기반으로 예측하는 대신, 우리는 포인트 이미지 피쳐와 고전적인 스테레오 매칭을 에뮬레이트하는 유사성 함수의 앙상블을 기반으로 예측한다.
따라서, 우리의 작업은 종단간 아키텍처 내에서 현대의 신경 렌더링과 고전적인 컴퓨터 비전을 결합한다.
SRF는 3D 암시적 형상 재구성, Implicit Feature Networks (IF-Nets)[6, 10] 및 Neural Distance Fields (NDF)[11]에 대한 이전 연구와 정신적으로 유사하며, 여기서 우리는 원래 제안된 점 좌표[9, 31, 36] 대신 입력에서 계산된 체적 심층 피쳐를 기반으로 점유 또는 부호 없는 거리를 디코딩한다.
우리의 연구는 또한 현대적 접근법과 통찰력을 공유한다[55, 56, 59].
마지막으로, 우리의 연구는 몇 가지 예를 들어 새로운 작업에 쉽게 적응할 수 있는 일반적인 표현을 배우는 것을 목표로 하는 평생 학습[53, 54]에서 영감을 얻었다.
우리는 새로운 장면으로 쉽게 일반화되는 일반적인 뷰 합성 네트워크를 학습한다.
테스트 예제에 대한 간단한 미세 조정으로 새로운 장면에 적용하면 결과가 더욱 향상된다.
3. Method
이 섹션에서는 학습 중에 보이지 않는 객체의 희소하고 분산된 입력 뷰가 주어지면 새로운 뷰 합성을 위한 우리의 방법Stereo Radience Fields (SRF)로 제시한다.
먼저 섹션 3.1의 배경을 설명한 다음 섹션 3.2의 이러한 통찰력을 바탕으로 SRF를 구축합니다.
3.1. Background
3.1.1 Generalizing Neural Radiance Fields (NeRF)
타겟 뷰의 픽셀에서 색상을 생성하기 위해 카메라 위치에서 픽셀을 통해 장면으로 레이를 촬영합니다.
우리는 레이를 동일한 길이의 bin으로 이진화하고 각 bin 내에서 3D 포인트 하나를 랜덤으로 샘플링한다.
각 지점 p ∈ R^3에서 색상 c ∈ {0, ..., 255}^3과 밀도 σ ∈ R을 예측한다.
밀도는 표면 영역(표면이 있는 곳에서는 높고 다른 곳에서는 낮음)을 인코딩합니다.
밀도에 따라 가중치를 부여하면, NeRF[34]에 따라 레이를 따라 색상 값이 볼륨 렌더링에 의해 최종 픽셀 색상으로 융합됩니다.
NeRF는 주어진 공간 위치 p와 뷰 방향 d에 대해 출력(c, σ)을 학습하여 신경 함수 f가 있는 장면을 기억한다
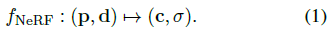
이것은 조밀한 뷰가 있는 단일 장면에 적합합니다.
그러나 점 좌표는 장면별 정보를 전달하지 않기 때문에 새로운 장면으로 일반화하지 못한다.
신경망 자체가 장면 표현이 된다(그림 2-(a)).
대신, 우리는 내부적으로 멀티 뷰 스테레오 재구성 및 합성을 에뮬레이트하고 테스트 시 장면 자체에서 조건화하는 신경 모델을 학습하는 것을 목표로 한다(그림 2-(b)).
이를 위해, 우리는 장면별
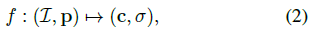
이 아닌 완전히 다른 포인트 인코딩 아키텍처를 사용한다,. 여기서 I = {I_i}^N_(i=1)은 알려진 카메라 매개 변수를 가진 N개의 참조 이미지 세트이다.
이 디자인은 클래식 스테레오에서 영감을 받았고 섹션 3.2에 설명되어 있다.
뷰 의존적 효과는 고려하지 않으며 향후 작업을 위해 남겨둡니다.
이를 통해 새로운 장면과 희소 입력에 대한 일반화에 집중할 수 있다.
3.1.2 Classical Multi-View Stereo
고전적인 스테레오 이미징 접근 방식(Structure-from-Motion, Multi-View Stereo)과 우리의 방법은 다음과 같은 관찰이다: 폐색이 없는 경우, 물체의 표면 3D 지점은 다중 뷰의 해당 광도계적으로 일관된 이미지 영역에 투영되는 반면, 비표면 3D 지점은 해당되지 않는 다른 영역에 착지한다(그림 3).
이 관찰을 반전하여 이미지에서 표면을 찾을 수 있습니다: 우리는 뷰에서 해당하는 영역을 찾아 삼각측량을 통해 3D 표면점을 찾을 수 있습니다.
고전 연구에서, 이것은 미분 되지 않는 다단계 엔지니어링 파이프라인에서 수행된다.
첫째, 유익하고 독특한 관심 영역이 발견됩니다.
그런 다음 관심 지점의 피쳐 설명자가 로컬 이미지 피쳐인 c.f. SIFT [26]에서 생성됩니다.
여러 이미지의 설명자가 유사성 측도에 따라 일치합니다.
SRF는 내부적으로 (렌더링 loss만을 기반으로) 종단간 unsupervised 방식으로 통신 매칭을 모방한다.
우리의 포인트 피쳐 설명자는 2D CNN 이미지 인코더 네트워크에 의해 학습된다.
고전적인 대응 소견은 포인트 설명자를 쌍으로 처리하여 SRF에서 에뮬레이트된다.
3.2. Stereo Radiance Fields (SRF)
SRF는 주어진 3D 공간에서 I = {I_i}^N_(i=1), 알려진 카메라 매개 변수를 사용하여 N개의 참조 이미지 세트인 I_i의 점 p에서 색과 밀도를 예측한다.
우리는 고전적인 멀티 뷰 스테레오 접근 방식과 유사하게 SRF, f를 구성한다:
(1) 점 p의 위치를 인코딩하기 위해 각 참조 뷰, I_i에 투영하고 로컬 피쳐 설명자 I_i(p), (섹션 3.2.1)를 구축한다.
(2) p가 표면에 있고 사진과 일치하는 경우 I_1(p), ..., I_N(p)이 일치해야 한다(그림 3); 피쳐 일치는 학습된 피쳐인 g_stereo로 에뮬레이트되어 모든 참조 뷰에서 피쳐를 인코딩한다(섹션 3.2.2).
(3) 인코딩은 학습된 디코더, dec에 의해 NeRF [34] 표현(섹션 3.2.3)으로 디코딩된다.
공식적으로, 이것은 SRF를 다음과 같이 분해한다:
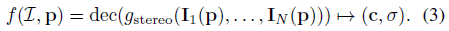
그림 4는 우리의 방법에 대한 개요를 제공한다.
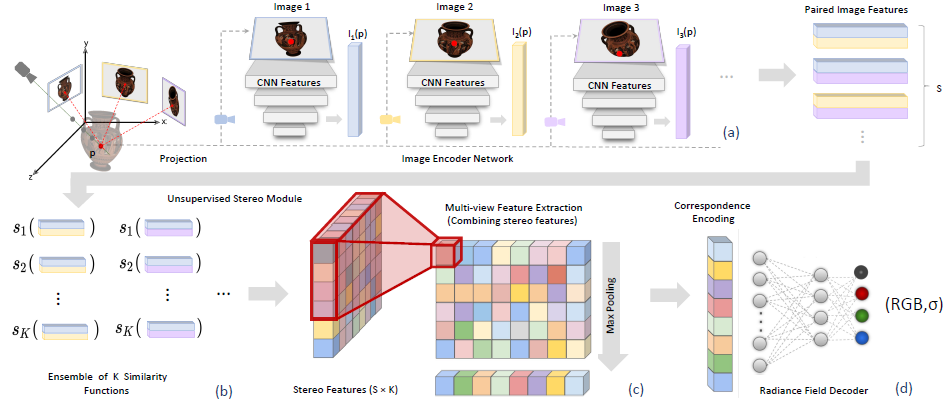
3.2.1 Image Encoder Network
입력이 장면별 정보가 없는 점 좌표인 NeRF와 대조적으로, 우리는 참조 이미지에 대한 예측을 조절한다.
우리는 각 참조 뷰, I_i에 p를 투영하고 로컬 피쳐 설명자 I_i(p)를 구축하여 이를 달성한다.
이를 위해 먼저 공유 2D CNN으로 각 전체 참조 이미지를 인코딩한다.
우리는 점 p 투영 위치의 각 CNN 레이어에서 심층 피쳐를 추출하여 I_i(p)를 구축한다.
2D CNN은 첫 번째 계층의 로컬 정보를 높은 수용 필드를 가진 이후 계층의 전역 정보까지 자연스럽게 인코딩하므로, 이는 I_i(p)를 다중 스케일 피쳐 설명자로 만든다(그림 4-(a) "이미지 인코더 네트워크").
점 투영은 연속 공간에 있는 반면 피쳐는 이산 그리드에 있기 때문에 추출에 이중 선형 보간을 사용한다.
p가 이미지 외부에 투영될 때 우리는 제로 패딩을 사용합니다.
자세한 내용은 부록을 참조하십시오.
3.2.2 Unsupervised Stereo Module
우리는 멀티 뷰 스테레오의 직관을 기반으로 한다: 3D 점 p가 photo-metrically 일관된 영역에 투영될 때 p는 표면에 있을 가능성이 높으므로 고밀도를 예측해야 한다.
임의의 수의 뷰를 처리하기 위해 스테레오 모듈은 뷰의 피쳐 설명자를 쌍으로 처리합니다.
구체적으로, 우리는 네트워크가 통신 검색 또는 이미지 색 전파에 유용한 이미지 점수를 학습할 수 있도록 하는 피쳐 쌍 I_i(p), I_j(p):
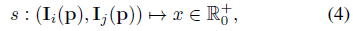
의 매핑을 학습하는 것을 목표로 한다.
참고로, 우리의 공식은 유사성 계산과 유사한 쌍별 처리를 기반으로 하지만, 대응성은 명시적으로 계산되지 않는다.
우리는 단일 뉴런을 사용하여 네트워크에서 각 매핑을 표현한다.
실제로, i, j ∈ 1, ..., N, i ≠ j를 갖는 가능한 각 쌍(I_i(p), I_j(p))은 ReLU 비선형성을 갖는 뉴런에 입력되어 음이 아닌 출력을 보장한다(그림 4-(b)).
그러면 크기 S = N^2 - N의 벡터 x가 생성되며, 한 쌍에 하나의 항목이 생성됩니다.
단일 뉴런에만 의존하는 대신, 우리는 s_k(·,·), k = 1 . . . K라는 뉴런 은행을 같은 방식으로 적용한다.
각각의 뉴런은 서로 다른 유사성을 배우거나 색을 전파하는 것을 전문으로 할 수 있다.
우리는 뱅크에 있는 각 뉴런의 출력 벡터 x_k를 스테레오 피쳐 매트릭스 X = [x_1 . . . x_K] ∈ R^(S×K)로 연결하는데, 높이는 쌍의 수이고 폭은 사용된 뉴런의 수이다(그림 4-(b) "스테레오 피쳐").
스테레오 피처 매트릭스는 피처 쌍을 매트릭스에 배열하고 뉴런 뱅크와 컨볼루션하여 효율적으로 계산할 수 있다.
그러나 쌍별 사진 일관성은 표면 점을 식별하기에 충분하지 않다.
3D 포인트는 참조 뷰가 근처에서 캡처되지만 세 번째 뷰에는 캡처되지 않을 때 스테레오 쌍의 사진 일치 이미지 영역에 투영될 수 있습니다.
우리는 뷰 쌍의 방향을 따라 스테레오 피쳐 매트릭스를 컨볼루션하여 다중 뷰의 정보를 집계한다.
구체적으로, 높이 방향으로 4쌍과 폭 방향을 따라 모든 유사성 측정을 집계한다(그림 4-(c) "멀티 뷰 피쳐 추출").
뷰 쌍 정보를 단일 벡터 y ∈ R^K로 병합하기 위해 뷰 방향으로 맥스 풀링을 실행한다.
설계상 완전 스테레오 모듈은 학습과 테스트 중에 다양한 수의 입력 뷰에 대해 유연하다는 점에 유의하십시오: 맥스 풀링 단계는 다양한 수의 입력 뷰가 주어졌을 때 고정 차원 K의 벡터를 계산한다.
이것은
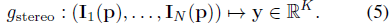
로 표시된 unsupervised 스테레오 모듈을 구성한다.
3.2.3 Radiance Field Decoder
네트워크의 마지막 단계는 포인트 p의 스테레오 인코딩 y = g_stereo(I_1(p), ..., I_N(p))를 최종 색상 c와 밀도 σ로 디코딩하는 것이다.
이를 위해, 우리는
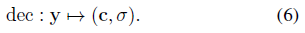
로 표시된 간단한 MLP 네트워크에 의존한다.
레이를 따라 샘플링된 색상은 볼륨 렌더링 후 밀도에 따라 융합됩니다 [28, 34].
네트워크의 학습은 스테레오 모듈에 대한 3D 데이터나 supervision 없이 멀티뷰 이미지만을 사용하여 완전히 종단간으로 이루어진다(그림 4-(d)).
우리는 렌더링된 예측과 타겟 이미지를 비교하기 위해 L2 loss를 사용한다.
추가 아키텍처 세부 정보는 부록을 참조하십시오.
4. Experiments
우리는 먼저 다양한 일반 객체와 장면에 대해 학습될 때 SRF의 일반화 능력을 연구한다.
섹션 4.1에서, 우리는 우리의 모델이 임의로 퍼져 있는 희박한 수의 뷰만 고려할 때 새로운 장면에 적용 가능한 일반화 구조를 실제로 학습한다는 것을 관찰한다.
또한, 우리는 섹션 4.2에 나온 것처럼 뷰 합성 작업에 대한 학습을 받았음에도 불구하고 우리 모델이 10개의 뷰에서만 3D 색상 메시를 생성할 수 있다는 것을 발견했다.
이러한 관찰은 기하학과 데이터를 통합하는 것이 일반화에 도움이 된다는 것을 시사한다.
마지막으로, 섹션 4.3에서는 제한된 시간 동안 단일 객체에서 학습한 경우에도 SRF의 다중 뷰 구조가 자연스럽게 일반화된다는 것을 보여준다.
Data.
우리는 공개적으로 사용 가능한 DTU Multi-View Stereopsis 데이터 세트[1]에 대한 실험을 수행한다.
그것은 매우 다양한 물체(예: buildings, statues, groceries, fruits, bricks, 등)를 포함하여 124개의 다른 장면으로 구성되어 있다.
장면을 테스트, 검증 및 학습 분할로 나눕니다(자세한 내용은 부록 참조).
우리는 SRF에 대한 입력으로 장면의 10개 이미지를 랜덤으로 샘플링한다.
평가 및 학습 목적으로, 우리는 다른 뷰를 타겟 뷰로 샘플링한다.
Baselines
우리는 우리의 접근 방식을 NeRF[34]와 대조한다.
NeRF에는 장면별 최적화가 필요합니다.
우리는 10개의 입력 이미지를 사용하여 각 장면에 대해 NeRF 모델을 학습하기 위해 공개적으로 사용 가능한 코드를 사용한다.
장면별 모델을 학습하는 데 이틀이 걸렸습니다.
일단 학습을 받으면 새로운 관점을 합성할 수 있다.
우리는 또한 공개적으로 사용 가능한 기성 LLFF[33] 모델과 비교한다.
ours처럼 LLFF는 테스트 장면에 대한 일반화를 허용한다.
연속적인 3D 표현 대신 참조 이미지가 여러 depth 레이어로 슬라이스됩니다.
타겟 뷰를 합성하기 위해 인접한 참조 이미지가 타겟 뷰로 워핑되어 함께 혼합됩니다.
4.1. Unconstrained Generalization
이 실험에서는 보이지 않는 테스트 장면에서 새로운 뷰 합성을 수행할 수 있는 모델을 학습하는 것을 목표로 한다.
이를 위해 전체 DTU 데이터 세트의 랜덤 학습(109개 장면), 테스트(10개 장면) 및 검증(5개 장면) 분할을 샘플링한다(부록 참조).
우리는 단일 NVIDIA Quadro RTX 8000에서 약 3일 동안 검증 최소값에 도달할 때까지 방법을 학습한다.


테스트 시간에 새로운 장면의 10개 뷰만 고려할 때, 우리의 방법은 렌더링된 새로운 뷰에서 샤프한 객체를 생성할 수 있으며 베이스라인을 능가한다.
정성 분석은 그림 5에, 정량 분석은 표 1에 제시하였다.
우리의 접근 방식은 새로운 장면으로 즉시 일반화되며 희박하고 임의로 분산된 다중 뷰에서 작동할 수 있다.
각 NeRF 모델은 장면별 최적화에 2일이 걸린다.
대신, 기하학적 스테레오 매칭을 에뮬레이트하는 아키텍처 덕분에 SRF는 많은 장면에서 배울 수 있다.
우리는 이것이 희소 데이터에서 새로운 관점을 합성하는 데 중요하다는 것을 발견했다.
또한, 우리는 최적화된 장면 표현의 아이디어를 통해 기하학적 및 학습 개념을 풍부하게 할 수 있다.
이를 위해 짧은 시간 동안 모델을 미세 조정한다.
이로 인해 베이스라인에 비해 결과가 더 선명해질 뿐만 아니라 최적화 시간도 며칠에서 몇 분으로 단축됩니다.
우리는 그림 7(b)-(d)와 그림 5에서도 우리의 방법을 미세 조정하는 효과를 보여준다.
우리는 희소 및 분산 뷰에 대해 학습된 NeRF 모델이 그림 7-(f)에 나온 것처럼 퇴화된 결과를 초래할 수 있다는 것을 관찰한다.
자세한 내용은 부록을 참조하십시오.

마지막으로, 우리는 도전적인 BRDF와 반사 영역이 스테레오 매칭을 기반으로 한 우리의 방법에 문제를 제기할 수 있다는 것을 발견했다.
미세 조정이 일부 문제를 완화하는 데 도움이 된다는 것을 알 수 있습니다(그림 9).
우리가 식 2에서 삭제한 SRF에 뷰 의존 모델링을 도입하면 이 문제를 해결할 수 있으며 흥미로운 미래 작업 방향이 될 것이다.

4.2. Meshing Predictions
예측을 일치시키기 위해, 우리는 물체를 둘러싼 점들의 밀집된 격자에서 10개의 이미지에 조건화된 SRF를 평가한다.
SRF는 각 점의 색상과 밀도를 예측합니다.
그런 다음 그리드에서 밀도를 임계값으로 설정하고 Marching Cubes [25]를 실행하여 메시를 얻는다.
메시에서 찾은 각 정점에 대해 좌표를 가져와서 SRF에 입력하여 색상을 예측하고 메시에 추가합니다.
결과는 그림 6을 참조하십시오.

4.3. Natural Generalization Capability
이전에, 우리는 기하학과 데이터를 통합하는 것이 일반화에 도움이 된다는 것을 발견했다.
다음으로, 우리는 우리의 아키텍처가 설계에 의해 자연스럽게 일반화되는지 검증한다.
우리는 이를 위해 급진적인 설정을 취한다.
우리는 단 30분 동안 단일 물체(합성 트랙터[34])에서 학습하고 매우 다른 물체(NeRF 데이터의 마이크)의 새로운 뷰 합성을 검사한다.
우리는 그림 8과 같이 외관과 기하학적 구조의 큰 차이에도 불구하고 일반화를 관찰한다.

5. Discussion and Conclusion
우리는 고전적인 멀티 뷰 스테레오의 구성 요소를 에뮬레이트하도록 설계된 신경 뷰 합성 모델인 Stereo Radiance Fields를 소개했다.
포인트 방향 좌표를 기반으로 radiance와 색상을 예측하는 대신, 우리는 각 3D 포인트를 여러 뷰에 투영하고 피쳐를 추출하여 쌍으로 처리한다.
이것은 암시적 대응 계산을 허용하는 self-supervised 렌더링 loss에 의해서만 구동되는 점수의 앙상블을 학습한다.
이 프로세스는 뷰 합성을 위해 종단 간 학습 가능한 네트워크 내에서 고전적인 스테레오의 피쳐 일치를 에뮬레이트한다.
실험은 SRF가 여러 장면에서 공통 구조를 학습한다는 것을 보여준다.
우리는 DTU 데이터 세트의 여러 장면에서 SRF 모델을 학습시키고 SRF가 일반화되어 사실적인 이미지를 생성한다는 것을 보여준다.
또한, 조밀한 뷰가 필요한 이전 작업과 달리, 우리는 임의로 희소한 분산 10 뷰를 입력으로 사용한다.
우리는 이러한 타겟 10개 뷰에 대해 10-15분간 미세 조정한 후 결과가 더욱 향상된다는 것을 보여준다.
놀랍게도 희소 뷰 설정(10개 뷰)에서 우리의 접근 방식은 이틀 동안 새로운 장면에서 학습할 때에도 SOTA 방법을 크게 능가한다.
마지막으로, 우리는 SRF가 3D supervision을 사용하지 않고 컬러 메시를 허용하는 해석 가능한 3D 표현을 암시적으로 계산한다는 것을 보여준다.
요약하면 SRF는 고전적인 멀티 뷰 스테레오와 최근의 신경 렌더링 아이디어를 기반으로 하지만 통합된 종단 간 학습 가능한 아키텍처에 결합한다.
우리는 고전적인 기하학적 컴퓨터 비전과 신경 렌더링의 상호 작용이 흥미로운 방법이며, 이는 추가적인 탐구를 할 가치가 있다고 생각한다.
향후 연구는 도전적인 BRDF를 모델링하고 본질적으로 드문 야생 샘플에서 동적 장면의 4D 시공간 뷰 합성으로 확장할 수 있다.