2023. 11. 23. 19:03ㆍtext-to-3D
Score Jacobian Chaining: Lifting Pretrained 2D Diffusion Models for 3D Generation
Haochen Wang, Xiaodan Du, Jiahao Li, Raymond A. Yeh, Greg Shakhnarovich
Abstract
디퓨전 모델은 그래디언트의 벡터 필드를 예측하는 것을 학습합니다.
우리는 학습된 그래디언트에 체인 룰을 적용하고, 미분 가능한 렌더러의 자코비안을 통해 디퓨전 모델의 score를 역전파할 것을 제안하며, 이를 복셀 래디언스 필드로 인스턴스화합니다.
이 설정은 여러 카메라 시점의 2D score들을 3D score로 집계하고, 3D 데이터 생성을 위해 사전 학습된 2D 모델을 용도 변경합니다.
우리는 이 응용 프로그램에서 발생하는 분포 불일치의 기술적 과제를 파악하고, 이를 해결하기 위한 새로운 추정 메커니즘을 제안합니다.
우리는 대규모 LAION 5B 데이터 세트에서 학습된 최근 발표된 Stable Diffusion을 포함한 여러 기성 디퓨전 이미지 생성 모델에서 알고리즘을 실행합니다.
1. Introduction
우리는 이미지에 대한 사전 학습된 2D 디퓨전 생성 모델을 3D 데이터에 액세스할 필요 없이 래디언스 필드의 3D 생성 모델로 변환하는 방법을 소개합니다.
핵심 통찰력은 디퓨전 모델을 종종 데이터 log-likelihood의 score 함수로 언급되는 그래디언트 필드의 학습된 예측 변수로 해석하는 것입니다.
우리는 추정된 score에 체인 룰을 적용하여 Score Jacobian Chaining (SJC)이라고 이름 지었습니다.
Hyvärinen과 Dayan [15]에 따라, score는 데이터에 대한 로그-밀도 함수의 그래디언트로 정의됩니다.
다양한 패밀리의 디퓨전 모델 [12, 49, 51, 53]은 모두 ∇_x log p_σ (x) 모델링, 즉 노이즈 레벨 σ 에서의 디노이징 score로 [18, 21, 53] 해석될 수 있습니다.
가독성을 위해 디노이징 score를 score라고 합니다.
디퓨전 모델에서 샘플을 생성하는 데에는 큰 σ 레벨에서 작은 σ 레벨까지 score 함수를 반복적으로 평가하여 샘플 x가 점차 데이터 매니폴드에 가깝게 이동합니다.
데이터 분포가 어닐링된 σ 레벨 (ancestral sampler [12], SDE 및 probability-flow ODE [53] 등)과 일치하도록 스텝 사이즈를 정밀하게 제어하여 그래디언트 하강으로 느슨하게 해석할 수 있습니다.
디퓨전 모델 [12, 49]에 대한 다른 관점이 있지만, 여기서는 디퓨전 모델이 그래디언트 필드를 생성한다는 관점에서 주로 동기를 부여합니다.
당연히 물어야 할 질문은 체인 룰이 학습된 그래디언트에 적용될 수 있는가 하는 것입니다.
이미지에 대한 디퓨전 모델을 고려하십시오.
이미지 x는 매개 변수 θ, 즉 x = f(θ)를 사용하는 일부 함수 f에 의해 매개 변수화될 수 있습니다.
자코비안 ∂x/∂θ를 통해 체인 룰을 적용하면 이미지 x의 그래디언트를 매개 변수 θ의 그래디언트로 변환합니다.
사전 학습된 디퓨전 모델과 f의 다른 선택을 쌍으로 하는 많은 잠재적인 사용 사례가 있습니다.
이 연구에서 우리는 f를 미분 가능한 렌더러로 선택하여 사전 학습된 2D 자원만을 사용하여 3D 생성 모델을 생성함으로써 3D와 멀티뷰 2D의 연결을 탐구하는 데 관심이 있습니다.
많은 선행 연구들 [2, 58, 60]은 3D 데이터 세트들 [5, 23, 55, 59]을 학습시킴으로써 3D 생성 모델링을 수행합니다.
이 접근법은 포맷 모호성만큼이나 도전적인 경우가 많습니다.
3D 자산의 높은 데이터 획득 비용 [9]에 더하여, 보편적인 데이터 포맷이 존재하지 않습니다: 포인트 클라우드, 메시, 체적 래디언스 필드 등은 모두 계산 균형을 가지고 있습니다.
이러한 3D 자산에 공통적인 점은 2D 이미지로 렌더링될 수 있다는 것입니다.
역 렌더링 시스템 또는 미분 렌더러 [24, 26, 29, 34, 39]는 기본 3D 매개 변수 θ와 관련하여 카메라 시점 π에서 렌더링된 이미지 x_π의 야코비안 J_π, ∂x_π/∂θ에 액세스할 수 있도록 합니다.
우리의 방법은 미분 렌더링을 사용하여 여러 시점에 걸친 2D 이미지 그래디언트를 3D 자산 그래디언트로 집계하고 생성 모델을 2D에서 3D로 들어올립니다.
우리는 3D 자산 θ를 복셀에 저장된 래디언스 필드로 매개 변수화하고 볼륨 렌더링 함수로 f를 선택합니다.
핵심 기술적 과제는 렌더링된 이미지 x_π에서 디퓨전 모델을 직접 평가하여 2D score를 계산하면 out-of-distribution (OOD) 문제가 발생한다는 것입니다.
일반적으로 디퓨전 모델은 디노이저로 학습되며 학습 중에 노이즈가 많은 입력만 볼 수 있습니다.
반면, 우리의 방법은 최적화 동안 3D 자산에서 노이즈가 없는 렌더링된 이미지에 대한 디노이저를 평가해야 하며 이는 OOD 문제로 이어집니다.
이 문제를 해결하기 위해 노이즈가 없는 이미지에 대한 score를 추정하는 접근 방식인 Perturb-and-Average Scoring을 제안합니다.

경험적으로, 우리는 먼저 OOD 문제를 해결할 때 Perturv-and-Average Scoring의 효과를 검증하고 간단한 2D 이미지 캔버스에 대한 하이퍼 파라미터 선택을 탐구합니다.
여기서는 FFHQ 및 LSUN Bedroom에서 학습된 조건 없는 디퓨전 모델을 사용하는 데 대한 미해결 문제를 식별합니다.
다음으로, 우리는 그림 1과 같이 3D 생성을 위한 SJC를 수행하기 위해 웹 스케일 LAION 데이터 세트에서 사전 학습된 모델인 Stable Diffusion을 사용합니다.
우리의 기여는 다음과 같습니다:
• 체인 룰의 적용을 통해 2D 디퓨전 모델을 3D로 리프팅하는 방법을 제안합니다.
• 사전 학습된 디노이저를 사용할 때 OOD의 과제를 설명하고 이를 해결하기 위한 Perturb-and-Average Scoring을 제안합니다.
• 우리는 최적화를 위한 그래디언트로 Perturb-and-Average Scoring을 적용하는 것에 대한 미묘함과 미해결 문제를 지적합니다.
• 3D 텍스트 기반 생성 작업에 대한 SJC의 효과를 입증합니다.
2. Related Work
Diffusion models은 최근 인터넷 규모 데이터 세트 [10, 36, 42, 44–47]의 이미지 생성으로 발전했습니다.
디퓨전 모델은 VAE [12, 49] 또는 denoising score-matcher [51, 53, 56]로 해석될 수 있습니다.
특히 한 체제에서 학습된 모델은 다른 [18, 53]에서 추론 및 샘플링에 직접 사용될 수 있습니다; 실제로는 거의 동등합니다.
Neural radiance fields (NeRF)는 뷰 합성 및 표면 지오메트리 추정을 포함한 멀티뷰 3D 재구성 작업에서 탁월한 역 렌더링 알고리즘 제품군입니다 [31, 34, 40, 57, 61].
개념적으로, 3D 자산은 RGB 색상과 공간 밀도 τ의 밀집된 그리드로 표현되며 alpha compositing [32]과 유사한 방식으로 이미지로 렌더링됩니다.
NeRF는 신경망으로 (RGB, τ) 볼륨을 매개 변수화하지만, 3D로 네트워크를 밀도 있게 쿼리하는 것은 상당한 컴퓨팅 비용을 초래합니다.
대안적으로, Voxel NeRFs [6, 27, 54, 62]는 볼륨을 복셀에 저장하고 최종 작업 성능에서 loss가 없음을 관찰합니다 [54, 62].
복셀을 쿼리하는 것은 신경망의 피드 포워드 패스보다 훨씬 빠른 간단한 메모리 작업입니다.
여기서는 DvGO [54] 및 TensoRF [6]에 기초한 하이퍼 파라미터를 가진 사용자 지정 복셀 래디언스 필드를 사용합니다.
2D-supervised 3D GANs은 구조화되지 않은 2D 이미지만을 사용하여 3D 생성 모델을 학습하는 접근 방식을 개척했으며 데이터 측면에서 더 큰 확장성을 약속합니다.
이러한 방법은 모델이 생성하는 3D 자산을 직접 supervise하는 것보다 생성된 3D 자산의 2D 렌더링을 supervise하며 종종 adversarial loss를 사용합니다 [3, 4, 38, 48, 65].
다시 말해, 학습 데이터로서 이미지만 필요합니다.
그러나 그러한 3D 생성 모델을 처음부터 학습하는 것은 여전히 어렵습니다 [37].
최근의 경험적 평가는 대부분 사람과 동물의 얼굴에 남아 있습니다 [3].
우리의 방법은 그 반대입니다: 우리는 이미 많은 양의 2D 데이터에 대해 사전 학습된 이미지 생성 모델을 사용하여 3D 자산의 반복 최적화를 안내합니다.
최적화 기반 생성은 3D GAN에 비해 훨씬 느리지만 콘텐츠 다양성을 높이기 위해 Stable Diffusion [45]과 같은 강력한 기성 2D 생성 모델을 활용하는 것이 가능해집니다.
CLIP-guided, optimization-based 3D generative models은 2D 렌더링을 가이드함으로써 3D 자산을 최적화하는 유사한 철학을 공유합니다 [14, 16, 17, 20, 25, 33].
그 중 DreamFields [16] 및 PureClipNeRF [25]는 또한 NeRF를 미분 가능한 렌더러로 사용합니다.
이 경우 2D 가이던스는 사전 학습된 이미지-텍스트 매칭 모델인 CLIP [42]에서 가져온 것입니다.
이 작업은 이미지 렌더링이 사용자 제공 텍스트 프롬프트와 일치하도록 3D 자산을 최적화합니다.
CLIP은 2D 생성 모델 자체가 아니기 때문에 이러한 파이프라인은 일반적으로 실제 이미지와 매우 다르게 보이는 일부 추상 distill된 콘텐츠 [28]를 생성합니다.
이와는 대조적으로, 우리는 현실적으로 보이는 3D 콘텐츠를 만들기 위해 적절한 2D 생성 모델인 디퓨전 모델을 사용합니다.
DreamFusion.
연구와 독립적이고 동시적인 Poole et al. [41]의 최근 arXived 연구는 pseudo-코드 수준에서 우리의 접근 방식과 유사한 알고리즘을 제안합니다.
이와 달리, 그들의 절차는 Graikos et al. [11]의 수학적 설정을 사용하여 디퓨전 모델의 학습 loss를 최소화하는 이미지 매개 변수화를 검색합니다.
이와는 대조적으로, 우리의 작업은 2D score에 체인 룰을 적용함으로써 동기를 부여됩니다.
주요 차이점은 섹션 4.3에 요약되어 있습니다.
구현 측면에서, 우리는 close-sourced Imagen [46] 디퓨전 모델에 접근할 수 없습니다.
대신, 우리는 Rombach et al. [45]이 발표한 사전 학습된 Stable Diffusion 모델을 사용합니다.
DreamFusion과의 비교를 위해, 우리는 동일한 디퓨전 모델을 기반으로 하는 제3자 구현, 즉 Stable-DreamFusion과 함께 사용합니다.
3. Preliminaries
공통적인 표기법을 확립하기 위해 디퓨전 모델의 score 기반 관점을 간단히 검토합니다.
디퓨전 모델에 대한 VAE 문헌에 익숙한 독자들을 위해, 우리는 간결한 score 기반 공식 카드와 이러한 아이디어를 연결하기 위한 부록 섹션 A1의 자세한 내용을 제공합니다.
Denoising score matching.
p_data에서 추출한 샘플 Y = {y_i}의 데이터 집합이 주어졌을 때, 디퓨전 모델은 노이즈가 있는 샘플 y + σn과 y의 차이를 최소화함으로써 주로 디노이저 D를 학습하는 것을 중심으로 전개됩니다,
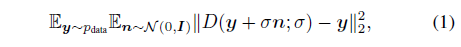
, 즉, σ값 범위에 대해 입력 y + σn의 디노이징합니다.
2D 이미지의 경우, D는 일반적으로 ConvNet으로 선택됩니다.
DDPM [12]과 같은 변종은 대신 노이즈 잔차 ^ε를 예측하기 위해 ConvNet을 매개 변수화했고, 이러한 모델은 [53]에 의해 디노이저의 형태로 다시 변환할 수 있습니다
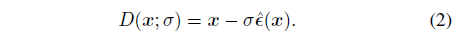
본 논문에서는 사전 학습된 모든 디퓨전 모델을 디노이저로 취급하고, 필요할 때 구현 시 인터페이스 변환을 수행합니다.
Score from denoiser.
p_σ(x)가 표준 편차 σ의 가우시안 노이즈에 의해 교란되는 데이터 분포를 나타낸다고 하자.
이전 연구들 [15, 51]에서는 식 (1)에 따라 학습된 디노이저 D가 디노이징 score에 대해 양호한 근사치를 제공한다는 것을 보여줍니다:
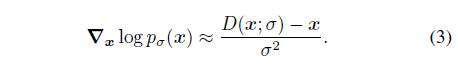
디노이징 디퓨전 모델은 다양한 σ ∈ {σ_i}^T_(i=1)에서 노이즈 분포 p_σ(x)의 score function을 추정합니다.
샘플링을 수행하기 위해, 디퓨전 모델은 σ_T > ... > σ_0 = 0의 노이즈 레벨의 시퀀스를 통해 샘플을 점진적으로 업데이트합니다.
{σ_i}는 경험적으로 선택되며, DDPM의 경우 일반적인 범위는 [0.01, 157] [12]입니다.
Score as mean-shift.
유용한 직관은 score가 mean-shift [7, 8]처럼 행동한다는 것입니다.
p_data를 i.i.d. 샘플 {y_i}에 대한 경험적 데이터 분포로 단순화하면 노이즈 레벨 σ에서 p_σ(x)는 가우시안의 혼합의 형태를 취합니다 [52]
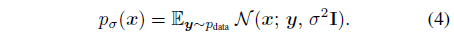
이 경우 최적 디노이저에 [18, 52]라는 닫힌 형태식이 존재합니다
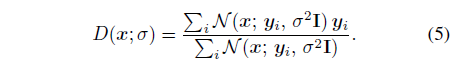
즉, D(x; σ)는 대역폭 σ를 가진 가우시안 커널에서 x 주위의 데이터 샘플 {y_i}의 로컬적으로 가중된 평균입니다.
디노이징 score 함수는 가중된 가장 가까운 이웃으로 이동하기 위해 x를 업데이트하는 방법에 대한 비모수적 가이드로 간주될 수 있습니다.
4. Score Jacobian Chaining for 3D Generation
여기서 θ는 3D 자산의 매개변수(예: 섹션 4.2에서와 같이 (RGB, τ)의 복셀 그리드)를 나타냅니다.
저희의 목표는 3D 장면을 생성하기 위해 분포 p(θ)에서 모델링하고 샘플링하는 것입니다.
저희의 설정에서는 이미지 p(x)에 대한 사전 학습된 2D 디퓨전 모델만 제공되고 3D 데이터에 액세스할 수 없습니다.
2D 및 3D 분포 p(x)와 p(θ)를 연관시키기 위해 3D 자산 θ의 확률 밀도는 카메라 포즈 π, 즉
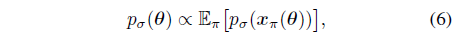
, 정규화 상수 Z = ∫E_π [p_σ (x_π(θ))]dθ까지, 에서 멀티뷰 2D 이미지 렌더링 x_π의 예상 확률 밀도에 비례한다고 가정합니다.
즉, 3D 자산 θ는 2D 렌더링 x_π만큼 가능합니다.
다음으로 Jenson's inequality를 사용하여 식 (6)의 분포에 하한 log ~p_σ(θ)를 설정합니다:
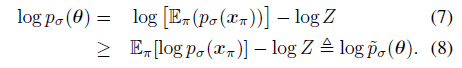
score는 데이터의 로그 확률 밀도의 그래디언트임을 기억하세요.
체인 룰에 의해

다음으로 사전 학습된 디퓨전 모델을 사용하여 실제 2D score를 계산하는 방법에 대해 논의합니다.
4.1. Computing 2D Score on Non-Noisy Images
식 (11)의 3D score를 계산하려면 x_π에 대한 2D score가 필요합니다.
첫 번째 시도는 식 (3), 즉
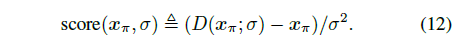
의 디노이저의 score를 직접 적용하는 것입니다.
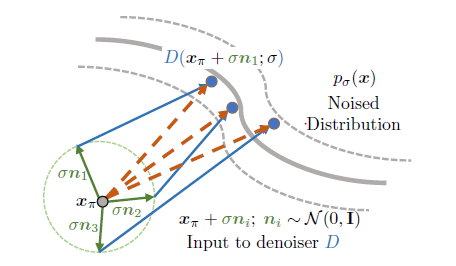
안타깝게도 x_π에서 사전 학습된 디노이저 D를 평가하면 out-of-distribution (OOD) 문제가 발생합니다.
식 (1)의 학습 objective에서 각 노이즈 레벨 σ에서 디노이저 D는 y ~ p_data 및 n ~ N(0, I)인 분포 y + σn의 노이즈가 많은 입력만 보았습니다.
그러나 3D 자산 θ에서 렌더링된 이미지 x_π는 일반적으로 이러한 분포와 일치하지 않습니다.

저희는 그림 2에서 이러한 OOD 상황을 설명합니다.
Baranchuk et al. [1]에 의해 FFHQ [19]에 대해 사전 학습된 디노이저가 주어지면 저희는 출력 D(x_blob; σ = 6.5)를 시각화합니다, 여기서 입력 x_blob은 회색 캔버스를 중심으로 주황색 blob을 보여주는 non-noisy 이미지입니다.
(5)에서 검토한 대로 D가 가중치가 부여된 가장 가까운 이웃을 예측한다는 직관 아래 디노이저가 주황색 blob과 얼굴 다양체를 혼합할 것으로 예상합니다.
그러나 실제로 저희는 이 score (D(x_blob; σ) - x_blob) / σ^2로 업데이트할 때 샤프한 아티팩트를 관찰하고 이미지는 얼굴 매니폴드에서 더 멀리 떨어집니다.
Perturb-and-Average Scoring.
OOD 문제를 해결하기 위해 저희는 Perturb-and-Average Scoring (PAAS)를 제안합니다.
입력에 노이즈를 추가한 다음 랜덤 노이즈에 대한 예측 score의 기대치를 고려하여 디노이저 D를 사용하여 노이즈가 없는 이미지 x_π의 score를 계산합니다
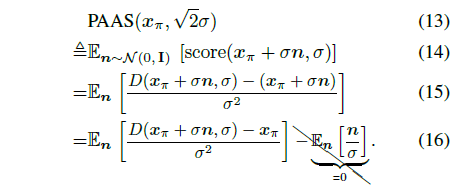
실제로 저희는 식 (16)의 기대치를 Monte Carlo 추정치를 사용합니다.
알고리즘은 그림 3에 나와 있습니다.
샘플링된 노이즈 {n_i} 집합이 주어지면 각 D(x_π + σ n_i)는 섭동된 입력 x_π + σ n_i에 대한 업데이트 방향을 제공합니다.
노이즈 섭동 {n_i}에 대해 평균을 내어 x_π 자체에 대한 업데이트 방향을 얻습니다.
Justifying PAAS in Eq. (13).
우리는 Perturb-and-Average Scoring이 √2σ의 팽창된 노이즈 레벨에서 x_π의 score에 대한 근사치를 제공한다는 것을 보여줍니다
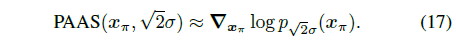

Proof. 식 (19)의 LHS는 두 가우시안의 컨볼루션이므로
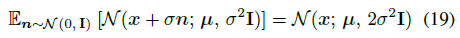
를 관찰합니다.
p_σ(x)는 식 (4)에 따라 가우시안이 혼합된 것임을 기억하십시오;
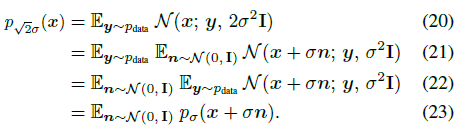
식 (23)의 양쪽 로그와 Jensen's inequality에 의해 우리는 식 (18)에 도착합니다.

Proof. Lemma 1의 RHS 그래디언트를 취함으로써
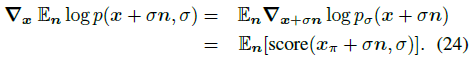
, 식 (13)에서 제안된 PAAS 알고리즘.
4.2. Inverse Rendering on Voxel Radiance Field
2D score 계산이 해결됨에 따라 식 (11)에서 설정의 나머지 절반은 미분 가능한 렌더러의 자코비안에 액세스해야 합니다.
3D Representation.
저희는 3D 자산 θ를 복셀 래디언스 필드 [6, 54, 62]로 표현하는데, 이는 신경망 [34]에 의해 매개변수화된 vanilla NeRF에 비해 액세스 및 업데이트가 훨씬 빠릅니다.
매개변수 θ는 밀도 복셀 그리드 V^(density) ∈ R^(1 x N_x x N_y x N_z)와 외관 피쳐의 복셀 그리드 V^(app) ∈ R^(c x N_x x N_y x N_z)로 구성됩니다.
일반적으로 외관 피쳐는 단순히 RGB 색상과 c = 3입니다.
단순화를 위해 이 작업에서는 뷰 종속성을 모델링하지 않습니다.
Inverse Volumetric Rendering.
이미지 렌더링은 각 픽셀을 통해 카메라 ray을 따라 독립적으로 수행됩니다.
우리는 카메라 ray를 길이 d의 동일하게 거리가 먼 세그먼트로 절단하고 i번째 세그먼트의 시작에 해당하는 공간 위치에서 삼선 보간을 사용하여 색상 및 밀도 그리드에서 (RGB_i; τ_i) 튜플을 샘플링합니다.
이 값들은 볼륨 렌더링 직교 [32]를 사용하여 픽셀 색상 C = ∑_i w_i · RGB_i로 알파 합성으로 지정되며, 여기서
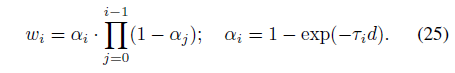
θ의 볼륨 렌더링은 직접적으로 구분할 수 있습니다.
렌더링된 이미지 x_π에서 PAAS(x_π)와 자코비안 J_π = ∂x_π/∂θ 사이의 식 (11)의 벡터-자코비안 곱은 식 (25)를 통해 점수를 역전파하여 계산됩니다.
이 벡터-야코비안 곱은 복셀 래디언스 필드에서 생성 모델링에 필요한 3D 그래디언트를 제공합니다.
Regularization Strategies.
복셀 그리드는 체적 렌더링을 위한 매우 강력한 3D 표현입니다.
노이즈가 많은 2D 가이던스가 주어지면 모델은 작은 밀도로 전체 그리드를 채워 한 뷰의 결합된 효과가 그럴듯한 이미지를 환각하도록 함으로써 부정행위를 할 수 있습니다.
저희는 일관된 3D 구조의 형성을 장려하기 위한 몇 가지 기술을 제안합니다.
Emptiness Loss:
이상적으로는 물체를 제외하고는 공간이 거의 0의 밀도로 희박해야 합니다.
우리는 ray r의 희소성을 장려하기 위해 emptiness loss를 제안합니다:
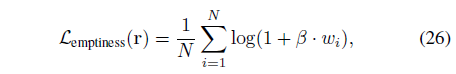
, 여기서 w_i는 (25)에 표시된 알파 합성 가중치입니다.
로그 함수의 모양은 작은 가중치가 시작될 때 심각한 페널티를 부과하지만 가중치가 크면 공격적으로 증가하지 않습니다.
이는 작은 밀도를 제거하는 우리의 목표와 일치합니다.
하이퍼파라미터 β는 loss 함수의 가파른 정도를 0 근처에서 제어합니다.
β가 클수록 밀도가 낮은 노이즈를 제거하는 데 더 중점을 둡니다.
β = 10을 설정합니다.
Emptiness Loss Schedule:
저희는 emptiness loss의 기여를 제어하기 위해 하이퍼파라미터 λ를 사용합니다.
큰 emptiness loss를 적용하면 학습 초기 단계에서 지오메트리 학습을 방해합니다.
그러나 빈 공간이 너무 작으면 floating 밀도 아티팩트가 발생합니다.
저희는 이 문제를 해결하기 위해 2단계 노이즈 제거 일정을 채택합니다.
첫 번째 K 반복에서 저희는 상대적으로 작은 가중 계수 λ_1을 사용합니다.
K^번째 반복 후에는 더 큰 λ_2로 증가합니다.
저희의 실험에서 λ_1 = 1 x 10^4 및 λ_2 = 2 x 10^5입니다.
저희는 효과를 보여주기 위해 그림 7에서 이 기술에 대한 ablation 연구를 제공합니다.

Center Depth Loss:
때때로 최적화는 객체를 장면 중심에서 멀어지게 합니다.
객체가 작아지거나 이미지 경계 주변을 배회합니다.
이런 일이 발생하는 몇 가지 경우에 대해 center depth loss (27)을 적용합니다, 여기서 D는 depth 이미지, B는 이미지 중심에 있는 상자(픽셀 위치 집합), B^C는 그 보완입니다.
4.3. SJC vs. DreamFusion
이 섹션에서는 SJC와 DreamFusion의 차이점과 연결점에 대해 설명합니다.
Differences from DreamFusion.
공식화 측면에서 θ에 대한 DreamFusion의 그레디언트 계산에는 U-Net 자코비안 항이 포함됩니다(논문 [41]의 식 2 참조).
실제로 그들은 "found that omitting the U-Net Jacobian term".
반면, 이 U-Net 자코비안 항은 우리의 공식에 나타나지 않습니다.
부록에 있는 그들의 추가 정당성은 실제로 우리의 관점에 더 의존합니다.
DreamFusion[41]을 넘어 우리의 추가 기여는 렌더링된 이미지에 디노이저를 사용할 때 OOD 문제가 미치는 영향에 대한 분석과 이를 해결하기 위한 PAAS 방법입니다.
분산 감소 기술, 즉 식 (16) 또는 ^ε - ε (DreamFusion에서) vs. 식 (15)에 대한 Monte-Carlo 추정치의 사용의 경우 3D 생성에 대해 경험적으로 두 방법 간에 유사한 성능을 관찰했습니다.
Influences by DreamFusion.
이 제출 당시 DreamFusion은 동시 arXiv 논문입니다.
그러나 저희가 논문을 읽었을 때, 저희 연구는 그들의 보고된 관찰에 영향을 받았습니다.
특히, 저희는 더 쉬운 하이퍼파라미터 튜닝을 위해 3D 최적화 중 σ의 랜덤 스케줄링 개념을 채택했으며, 전체 3D 품질을 향상시키는 뷰 증강 언어를 사용했습니다.
향후 작업을 위해 저희는 뷰 의존적 프롬프트보다 더 일반적인 해결책을 모색하기를 희망합니다.
5. Experiments
우리는 SJC의 특성을 보다 포괄적으로 이해하기 위해 무조건적 디퓨전 모델과 조건적 디퓨전 모델 모두에 대한 실험을 수행합니다.
DDPMs trained on FFHQ and LSUN Bedroom은 Dhariwal과 Nichol [10]의 구현을 기반으로 하는 아키텍처를 가진 무조건적인 디퓨전 모델입니다.
그들은 256x256의 이미지 해상도로 학습되었습니다.
FFHQ [19]는 성별, 연령, 인종, 얼굴 외모뿐만 아니라 머리 포즈에 대한 다양한 범위를 가진 정렬된 얼굴의 데이터 세트입니다.
LSUN Bedroom [63]에는 다양한 가구 레이아웃 계획과 풍부한 인테리어 디자인 스타일이 포함된 침실 이미지가 포함되어 있습니다.
Stable Diffusion은 Rombach et al. [45]이 개발한 Latent Diffusion Model (LDM)을 기반으로 한 확장된 작업입니다.
이는 LAION5B 데이터 세트에서 학습되었습니다 [47].
저희는 릴리스 버전 v1.5를 사용합니다.
디퓨전은 4x64x64의 잠재 공간에서 수행된 다음 디코더에 의해 3x256x256으로 업샘플링됩니다.
이 모델은 기본적으로 텍스트 조건화된 이미지 생성을 위해 학습되었으며 언어 조건화의 강도를 제어하는 안내 스케일 매개변수를 노출합니다 [13].
직관적으로 더 큰 가이던스 스케일은 샘플 다양성을 절충하여 조건화된 이미지 분포를 텍스트 프롬프트에 더 충실하게 만듭니다.
5.1. Validating PAAS on 2D images.
3D 생성으로 직접 뛰어들기 전에 먼저 PAAS가 간단한 2D 이미지 캔버스에 효과적인 가이던스를 제공하는지 확인합니다.
즉, 여기서 θ는 RGB 값의 그리드이고 f는 항등 함수입니다.
PAAS에 의해 생성된 벡터 필드의 경사 하강이 고품질 이미지를 생성하는 것이 희망입니다.
여기서 중요한 결정을 내려야 할 것은 PAAS를 계산하는 {σ_i}의 일정입니다.
저희는 DreamFusion에서 제안한 대로 어닐링된 스케줄(어닐링된 σ) vs. 랜덤 스케줄(랜덤 σ)을 사용하여 실험했습니다.
어닐링된 σ 스케줄에서는 큰 σ에서 시작하여 이미지 캔버스 x를 업데이트함에 따라 점차 감소합니다.
더 큰 σ 레벨에서 계산된 PAAS는 높은 수준의 이미지 구조에 적용되는 반면, 더 작은 σ는 세부 기능에 대한 더 강력한 가이던스를 제공합니다.
반대로 랜덤 σ 스케줄은 모든 단계에서 균일하게 σ를 샘플링합니다.
저희는 그림 4에서 정성적 비교를 보여줍니다.

FFHQ로 학습된 무조건적 디퓨전 모델의 경우 어닐링된 σ가 랜덤 σ보다 성능이 우수하고 이미지 샘플의 포즈 변화와 품질이 더 우수하다는 것을 관찰했습니다.
특히 랜덤 σ는 평균 얼굴로 수렴하는 심각한 모드 추구 행동을 나타냅니다.
LSUN Bedroom의 경우 모드 추구 행동으로 인해 내용물이 없는 블러한 이미지 캔버스가 생성됩니다.
반면 자연어 프롬프트는 Stable Diffusion으로 이미지를 샘플링할 때 중요한 역할을 합니다.
언어 가이던스가 3.0의 정규 수준으로 설정되면 관찰 결과가 FFHQ 및 LSUN의 샘플링과 대체로 일치합니다.
랜덤 σ 스케줄은 블러한 출력을 생성합니다.
그러나 가이던스 척도가 10.0으로 업그레이드되면 랜덤 σ 스케줄이 선명하고 깨끗한 이미지를 생성하기 시작하고 어닐링된 σ 스케줄보다 성능이 뛰어납니다.
어닐링된 σ 스케줄링에 대한 다양한 정교한 전략에도 불구하고(자세한 내용은 코드 참조), 높은 언어 가이던스 규모에서 랜덤 σ가 더 나은 옵션으로 남아 있습니다.
저희는 더 강력한 언어 가이던스가 이미지 분포를 좁게 만들고 모드를 찾는 알고리즘에 더 유리하게 만든다고 가정합니다.
저희는 그림 4의 이미지 중 어떤 것도 표준 디퓨전 추론 파이프라인의 샘플 품질과 일치할 수 없으며 최적화를 위한 그래디언트로 PAAS를 적용하는 올바른 방법은 여전히 미해결 문제로 남아 있습니다.
5.2. 3D Generation
이 논문에서는 언어 조건적 Stable Diffusion 모델을 사용한 3D 생성에 초점을 맞춥니다.
3D 도메인의 FFHQ 및 LSUN bedroom에서 어닐링된 σ 스케줄을 조정하는 것이 실제로는 어렵다는 것을 발견하고 향후 작업으로 남깁니다.
앞서 2D 실험에서 얻은 통찰력을 바탕으로 높은 언어 가이던스 척도와 결합된 랜덤 σ 스케줄을 사용합니다.
Rendering with Latent 3D Features.
Stable Diffusion은 사전 학습된 AutoEncoder의 잠재 피쳐에 대한 디퓨전 모델링을 수행하여 계산을 효율화합니다.
따라서 R^(4 x N_x x N_y x N_z)의 복셀 그리드로 표시되는 피쳐 필드 [3, 38]에서 잠재 공간에 피쳐 이미지를 렌더링하도록 선택합니다.


Qualitative Comparison.
그림 5에서는 SJC의 텍스트 프롬프트 3D 생성 결과를 보여줍니다.
동물에서 시드니 오페라 하우스에 이르기까지 다양한 프롬프트 세트에 걸쳐 복잡한 3D 모델을 생성할 수 있습니다.
다음으로 SJC를 사전 학습된 동일한 Stable Diffusion 모델을 기반으로 한 타사 구현인 Stable-DreamFusion과 비교합니다.
그림 6에서는 동일한 프롬프트가 주어지면 생성된 3D 자산의 질적 비교를 보여줍니다.
저희는 SJC가 상당한 수의 경우 Stable-DreamFusion보다 더 나은 이미지 품질과 더 합리적인 구조로 3D 모델을 생성하는 것을 관찰했습니다.
저희는 두 시스템 모두 다양한 시도에 걸쳐 품질 변동이 있음을 인정하며, 이 비교의 요점은 전체 파이프라인이 경쟁력이 있음을 보여주는 것입니다.

Ablations.
그림 7에서 저희는 제안된 emptiness loss의 중요성과 섹션 4.2에서 논의된 가중치 λ의 스케줄링을 입증하기 위해 albations를 수행합니다.
저희는 제안된 λ에 비해 일정한 가중치 λ를 사용하여 emptiness loss가 없는 결과를 보여줍니다.
저희는 완전한 방법 (Ours)이 생성된 3D 모델의 품질을 향상시키는 것을 관찰했습니다, 예를 들어, 더 적은 플로팅 아티팩트와 더 나은 지오메트리를 개선합니다.
6. Conclusion
저희는 사전 학습된 이미지(2D) 디퓨전 모델에서 3D 자산을 생성하기 위한 최적화 기반 접근 방식을 제안합니다.
주요 기술적 기여는 디노이징-학습된 디퓨전 모델과 디퓨전에 의해 가이드되는 3D 모델을 최적화하는 과정에서 발생하는 노이즈가 없는 이미지 사이의 간격을 연결하는 Perturb-and-Average Scoring 방법의 도출입니다.
저희는 또한 생성된 3D 장면의 품질을 향상시키기 위한 새로운 정규화 loss를 제안합니다.
대규모 Stable Diffusion 모델을 사용하여 저희의 접근 방식이 사용 가능한 동시 작업에 비해 유리하게 강력한 3D 모델을 생성할 수 있음을 보여줍니다.
마지막으로, 저희는 무조건적 이미지 디퓨전 모델과 텍스트-조건적 모델에서 노이즈 스케줄링 방식의 효과 사이의 흥미로운 구별을 조사하고 향후 작업을 위한 방법을 확인합니다.