2025. 3. 24. 11:13ㆍ3D Vision/Urban Scene Reconstruction
CityGaussianV2: Efficient and Geometrically Accurate Reconstruction for Large-Scale Scenes
Yang Liu, Chuanchen Luo, Zhongkai Mao, Junran Peng, Zhaoxiang Zhang
Abstract
최근 3D Gaussian Splatting (3DGS)은 효율적이고 고충실도의 새로운 뷰 합성을 나타내며 래디언스 필드 재구성에 혁명을 일으켰습니다.
그러나 특히 크고 복잡한 시나리오에서 표면을 정확하게 표현하는 것은 3DGS의 비정형적인 특성으로 인해 여전히 중요한 과제로 남아 있습니다.
이 논문에서는 기하학적 정확성과 효율성과 관련된 중요한 문제를 해결하는 대규모 장면 재구성을 위한 새로운 접근 방식인 CityGaussianV2를 소개합니다.
2D Gaussian Splatting (2DGS)의 유리한 일반화 기능을 바탕으로, 우리는 그 수렴 및 확장성 문제를 다룹니다.
구체적으로, 우리는 블러 아티팩트를 제거하고 수렴을 가속화하기 위해 분해된 그래디언트 기반의 밀집화 및 뎁스 회귀 기법을 구현합니다.
확장을 위해 2DGS 변성으로 인한 가우시안 카운트 폭발을 완화하는 Elongation 필터를 도입합니다.
또한 병렬 학습을 위해 CityGaussian 파이프라인을 최적화하여 최대 10배 압축, 학습 시간 최소 25% 절약, 메모리 사용량 50% 감소를 달성했습니다.
우리는 또한 대규모 장면에서 표준 지오메트리 벤치마크를 확립했습니다.
실험 결과, 우리의 방법이 시각적 품질, 기하학적 정확성, 그리고 저장 및 학습 비용 사이에서 유망한 균형을 이루고 있음을 보여줍니다.
1 Introduction
3D 장면 재구성은 컴퓨터 비전과 그래픽스 분야에서 오랜 기간 동안 중요한 주제로 여겨져 왔습니다, 이는 사진-사실적인 렌더링과 정확한 지오메트리 재구성을 핵심 목표로 하고 있습니다.
Neural Radiance Fields (NeRF) (Mildenhall et al., 2021)를 넘어, 3D Gaussian Splatting (3DGS) (Kerbl et al., 2023)은 학습 수렴 및 렌더링 효율성에서 우수성을 인정받아 이 분야에서 주요 기술로 자리 잡았습니다.
3DGS는 장면을 이산 가우시안 타원체 세트로 표현하며, 고도로 최적화된 래스터라이저로 렌더링합니다.
그러나 이러한 프리미티브는 정렬되지 않은 구조를 가지며 실제 장면의 표면과 잘 일치하지 않습니다.
이러한 제한은 외삽된 뷰에서 합성 품질을 저하시키고 편집, 애니메이션 및 재조명에 대한 다운스트림 적용을 방해합니다 (Gu'edon & Lepetit, 2024).
최근에는 이 문제를 해결하기 위해 많은 우수한 작품들 (Gu'edon & Lepetit, 2024; Huang et al., 2024; Yu et al., 2024c)이 제안되었습니다.
단일 물체나 작은 장면에서 큰 성공을 거두었음에도 불구하고, 복잡하고 큰 장면에 직접 적용하면 악마가 나타납니다.


한편, 기존 방법들은 확장성 및 일반화 능력과 관련된 중요한 도전에 직면해 있습니다.
예를 들어, SuGaR (Gu'edon & Lepetit, 2024)은 가우시안과 메쉬를 결합하여 정제합니다.
그러나 대규모 및 복잡한 시나리오에서는 메시가 광범위하고 세밀하게 세부화되어 상당한 메모리 요구 사항과 용량 제한이 발생할 수 있습니다.
GOF (Yu et al., 2024c)는 대규모의 과도한 가우시안과 고군분투하고 있습니다.
이러한 가우시안은 렌더링 및 지오메트리 품질을 심각하게 저하시킬 뿐만 아니라 부록의 그림 7 및 그림 8에서 검증된 것처럼 제거하기 쉬운 쉘 모양의 메시를 생성합니다.
2DGS (Huang et al., 2024)는 표 1에서 볼 수 있듯이 더 나은 일반화 능력을 보이지만, 그림 1의 (b) 부분에 설명된 블러 가우시안에 의해 수렴이 방해받고 있습니다.
또한 병렬 학습을 통해 확장할 때 그림 3과 같이 가우시안 카운트 폭발을 겪습니다.
또 다른 도전 과제는 평가 프로토콜에 있습니다: 경계 영역에서의 관측이 불충분하기 때문에 기하학적 추정은 이러한 영역에서 오류가 발생하기 쉽고 불안정해집니다.
그 결과, 지표가 크게 변동하고 실제 성능을 과소평가할 수 있어 (Xiong et al., 2024) 알고리즘을 객관적으로 평가하고 비교하기 어렵습니다.




한편, 대규모 장면의 기하학적으로 정확한 재구성을 실현하기 위해서는 효율적인 병렬 학습과 압축을 달성하는 것이 매우 중요합니다.
표 2에서 볼 수 있듯이 병렬 학습 중에 가우시안의 총 수는 19.3M으로 증가할 수 있으며, 이로 인해 저장 용량이 4.6GB, 메모리 비용이 31.5GB로 증가하고 렌더링 속도는 25FPS 이하로 떨어집니다.
또한 기존의 VastGaussian (Lin et al., 2024)은 학습에 거의 3시간이 소요되며, CityGaussian (Liu et al., 2024)은 학습과 압축을 모두 완료하는 데 4시간이 소요됩니다.
저가형 장치나 엄격한 시간 제약 하에서 재구성할 경우, 이러한 학습 비용과 렌더링 속도는 용납될 수 없습니다.
따라서 경제적인 병행 학습 및 압축 전략이 시급히 필요합니다.
이러한 도전 과제에 대응하여, 우리는 대규모 장면 재구성을 위한 기하학적으로 정확하면서도 효율적인 전략인 CityGaussianV2를 소개합니다.
2DGS는 유리한 일반화 기능 덕분에 원시적인 것으로 간주됩니다.
재구성을 가속화하기 위해 Depth-Anything V2 (Yang et al., 2024)와 Decomposed-Gradient-based Densification (DGD)에 의해 유도된 뎁스 회귀를 사용합니다.
그림 1과 표 2의 (b) 부분에서 볼 수 있듯이, DGD는 성능 향상에 중요한 블러 surfels를 효과적으로 제거합니다.
확장성을 해결하기 위해 병렬 학습 중 2DGS 퇴화와 관련된 가우시안 카운트 폭발 문제를 완화하기 위해 Elongation 필터를 도입합니다.
단일 GPU의 부담을 줄이기 위해 CityGaussian의 블록 분할 전략을 기반으로 병렬 학습을 수행합니다.
그리고 우리는 CityGaussian의 시간 소모적인 후가지치기 및 distillation 단계를 생략하여 프로세스를 간소화합니다.
대신, 우리는 처음부터 2도의 구형 고조파를 구현하고 기여 기반 가지치기를 블록별 파인튜닝에 통합합니다.
그림 1의 (c) 부분에서 보여준 바와 같이, 복잡한 구조물의 표면 품질을 높이는 동시에 학습 비용을 크게 절감합니다.
또한 기여 기반 벡터 양자화를 통해 대규모 2DGS의 저장 요구 사항을 10배까지 줄일 수 있습니다.
평가를 위해, 우리는 관측되지 않은 지역을 효율적으로 배제하고 안정적이고 일관된 평가를 제공할 수 있는 가시성 기반 작물 부피 추정 전략과 함께 TnT-style (Knapitsch et al., 2017) 프로토콜을 소개합니다.
요약하자면, 우리의 기여는 네 가지입니다:
• 2DGS를 위한 새로운 최적화 전략은 대규모 장면에서 수렴을 가속화하고 대용량으로 확장할 수 있게 합니다 (섹션 3.2).
• 학습 비용과 저장 요구 사항을 크게 줄이면서 실시간 렌더링 성능을 가능하게 하는 고도로 최적화된 병렬 학습 파이프라인 (섹션 3.3).
• 대규모 무한 장면에 맞춘 TnT-style의 표준화 평가 프로토콜로, 대규모 장면 재구성을 위한 기하학적 벤치마크를 확립합니다 (섹션 4).
• 우리가 아는 한, 우리의 CityGaussianV2는 대규모 표면 재구성에서 가우시안 래디언스 필드를 구현한 최초 중 하나입니다. 실험 결과는 기하학적 품질과 효율성 모두에서 우리의 SOTA 성능을 확인시켜줍니다.
2 Related Works
2.1 Novel View Synthesis은 3D 장면 주변의 다양한 소스 시점에서 캡처한 이미지를 사용하여 이전에 보지 못한 시점에서 새로운 이미지를 생성하는 것을 목표로 합니다.
이 새로운 렌더링은 주로 장면의 재구성된 3D 표현을 기반으로 합니다.
이 분야에 가장 중요한 기여 중 하나는 multi-layer perceptions (MLP)을 사용하여 타겟 장면을 암묵적으로 모델링하는 Neural Radiance Fields (NeRF) (Mildenhall et al., 2021)입니다.
그 후, MipNeRF (Barron et al., 2021; 2022)는 안티에일리어싱 원추형 frustum 기반 렌더링을 도입하여 불쾌한 앨리어싱 아티팩트를 해결합니다.
Deng et al. (2022); Wei et al. (2021); Xu et al. (2022)은 모델 수렴을 가속화하기 위해 포인트 클라우드에서 depth supervision을 적용합니다.
InstantNGP (M ¨uler et al., 2022)로 대표되는 알고리즘은 멀티 해상도 해시 인코딩 그리드와 octrees (Zhang et al., 2023; Wang et al., 2022; Yu et al., 2021)를 포함한 단순화된 데이터 구조를 활용하여 NeRF의 학습 및 렌더링 속도를 높입니다.
최근에 등장한 3D Gaussian Splatting (Kerbl et al., 2023)은 NeRF의 학습 효율성과 렌더링 속도에 대한 단점을 극복합니다.
후속 연구는 3DGS에서 안티에일리어싱 Yu et al. (2024b), 저장 비용 Fan et al. (2023); Zhang et al. (2024c); Navaneet et al. (2023); Morgenstern et al. (2023), 고감도 영역 과소적합 기능 Bul`o et al. (2024); Zhang et al. (2024b)을 더욱 향상시킵니다.
이 주목할 만한 연구들은 우리 알고리즘 설계에 대한 귀중한 통찰력을 제공해 왔습니다.
2.2 Surface Reconstruction with Gaussians
정렬되지 않은 이산 3DGS에서 정확한 표면을 추출하는 것은 흥미롭지만 도전적인 작업입니다.
명확한 표면을 추출하고 매끄러움과 이상치를 정규화하기 위해 몇 가지 알고리즘이 개발되었습니다.
선구적인 SuGaR (Gu'edon & Lepetit, 2024)은 3DGS를 사전 학습하고 이를 추출된 메쉬와 결합하여 파인튜닝을 수행합니다.
그런 다음 빠른 메쉬 추출을 위해 포아송 재구성 알고리즘에 의존합니다.
최근 GSDF (Yu et al., 2024a)와 NeuSG (Chen et al., 2023)는 부호화된 거리 함수와 함께 3DGS를 최적화하여 정확한 표면을 생성합니다.
2DGS (Huang et al., 2024)와 동시 GaussianSurfels (Dai et al., 2024)은 모호한 뎁스 추정을 피하기 위해 1차원 3D 가우시안 프리미티브를 붕괴시킵니다.
렌더링과 뎁스 맵에서 파생된 노멀도 매끄러운 표면을 보장하기 위해 정렬됩니다.
TrimGS (Fan et al., 2024)는 부정확한 기하학적 구조를 제거하기 위해 새로운 가우시안별 기여 정의를 추가로 제공합니다.
후처리 기법으로 GS2Mesh (Wolf et al., 2024)는 사전 학습된 스테레오 매칭 모델을 사용하여 3DGS에서 직접 메시를 내보냅니다.
GOF (Yu et al., 2024c)는 무한한 장면에 중점을 둡니다.
레이-추적 기반 볼륨 렌더링을 활용하여 장면 내에서 연속적인 불투명도 분포를 얻습니다.
2DGS의 TSDF 기반 마칭 큐브 전략 대신 GOF는 불투명 필드에서 SDF를 가져와 마칭 사면체를 사용하여 메시를 추출합니다.
RaDeGS (Zhang et al., 2024a)는 가우시안과의 레이 교차점을 새롭게 정의하고, 그에 따라 곡면과 뎁스 분포를 도출합니다.
이러한 알고리즘은 작은 장면이나 단일 객체에서 성공적인 것으로 입증되었지만, 성능 저하, 밀도 안정성, 학습 비용 등 확장의 어려움은 아직 해결되지 않았습니다.
저희의 분석과 디자인이 커뮤니티에 대한 더 많은 인사이트를 제공할 수 있기를 바랍니다.
2.3 Large-Scale Scene Reconstruction
지난 수십 년 동안 대규모 이미지 컬렉션에서 3D 재구성이 상당한 주목을 받으며 큰 진전을 이루었습니다.
최신 알고리즘 (Tancik et al., 2022; Turki et al., 2022; Xiangli et al., 2022; Xu et al., 2023; Zhang et al., 2023; Li et al., 2024)은 주로 NeRF (Mildenhall et al., 2021)를 기반으로 합니다.
그러나 학습과 렌더링에 필요한 상당한 시간은 오랫동안 NeRF 기반 방법을 방해해 왔습니다.
최근 VastGaussian (Lin et al., 2024)으로 대표되는 3DGS의 부상은 대규모 장면 재구성의 패러다임 변화를 나타냅니다.
HierarchicalGS (Kerbl et al., 2024) 및 OctreeGS (Ren et al., 2024)와 같은 후속 개발에서는 다양한 규모의 장면을 효율적으로 렌더링할 수 있는 Level-of-Detail (LoD) 기법이 도입되었습니다.
CityGS (Liu et al., 2024)는 병렬 학습, 압축 및 LoD 기반 빠른 렌더링을 포괄하는 포괄적인 파이프라인을 제공합니다.
그리고 DoGaussian (Chen & Lee, 2024)은 Alternating Direction Methods of Multipliers (ADMM)을 적용하여 3DGS를 분산적으로 학습합니다.
한편, GrendelGS (Zhao et al., 2024)는 서로 다른 GPU의 블록 간 통신을 용이하게 하며, FlashGS (Feng et al., 2024)는 고도로 최적화된 렌더러를 통해 대규모 학습 및 렌더링을 위한 VRAM 비용을 크게 절감합니다.
이러한 발전에도 불구하고 신뢰할 수 있는 벤치마크의 부족으로 인해 기하학적 정확성 문제는 대부분 간과되고 있습니다.
우리의 연구는 이 격차를 해결하여 경제적 학습, 높은 충실도, 정확한 지오메트리를 위한 새로운 알고리즘과 함께 신뢰할 수 있는 벤치마크를 제안합니다.
3 Method
3.1 Preliminary
3D Gaussian Splatting (Kerbl et al., 2023)은 3D 가우시안 분포로 설명되는 타원체 집합, 즉 G_N = {G_n|n = 1, ...,N}을 가진 3D 장면을 나타냅니다.
각 가우시안에는 중심점 μ_n ∈ R^(3×1), 공분산 σ_n ∈ R^(3×3), 불투명도 σ_n ∈ [0, 1], spherical harmonics (SH) 피쳐 f_n ∈ R^(3×16)을 포함한 학습 가능한 속성이 포함되어 있습니다.
공분산 행렬은 스케일링 행렬 R_n과 회전 행렬 S_n, 즉 σ_n = R_n S_n^T R_n^T로 더 분해됩니다.
특정 픽셀 p에 대해 c_p 색상은 알파 블렌딩을 통해 도출됩니다: (1), γ(p)는 레이 교차 픽셀 p에 위치한 가우시안을 나타내며, x는 해당 쿼리 포인트입니다.
3DGS의 최적화를 supervise하는 loss L은 L1 loss L_1과 D-SSIM loss L_SSIM 두 부분의 가중 합입니다.
3DGS는 뷰-스페이스 위치 그래디언트 (예: ∇_densify = ∂L/∂μ_n)에 의해 유도되는 휴리스틱 적응 밀도 제어를 통해 과소 또는 과잉 재구성을 방지합니다.
그래디언트가 특정 임계값보다 큰 가우시안은 복제되거나 분할됩니다.
자세한 내용은 독자들에게 3DGS의 원본 논문을 참고하시기 바랍니다 (Kerbl et al., 2023).

CityGaussian (Liu et al., 2024)은 3DGS를 대규모 장면으로 확장하는 것을 목표로 합니다.
그림 4에 나타난 바와 같이, 먼저 전체 학습 데이터에 대해 대략적인 모델을 3DGS 일정으로 사전 학습합니다.
그 후, 가우시안 프리미티브와 학습 데이터를 겹치지 않는 블록으로 나누고 병렬 튜닝을 수행합니다.
그 후, LightGaussian (Fan et al., 2023)의 접근 방식을 채택하여 프루닝에 30,000회, distillation에 10,000회를 추가로 적용합니다.
프루닝은 렌더링 중요도에 따라 중복된 가우시안을 제거하는 반면, distillation은 spherical harmonic (SH) 차수를 3에서 2로 줄입니다.
그런 다음 저장 압축을 위해 벡터 양자화를 수행합니다.
2D Gaussian Splatting (Huang et al., 2024)은 3D 타원체 부피를 surfels로 알려진 2D 방향 가우시안 디스크 세트로 축소하여 3DGS의 표면 추정 모호성을 해결합니다.
그 공분산은 두 개의 접선 벡터 t_(n,u)와 t_(n,v), 그리고 스케일링 벡터 S_n = (s_(n,u), s_(n,v))로 특징지어집니다.
또한, 2DGS는 뎁스 왜곡 정규화를 포함하고 표면 평활도 loss L_Normal을 적용하여 뎁스 맵에서 추정된 서펠 노멀과 정렬합니다.
이러한 향상은 기하학적 재구성과 새로운 뷰 합성에서 우수한 결과를 가져옵니다.
3.2 Optimization Mechanism
이 섹션에서는 수렴 가속과 안정적인 학습을 위한 최적화 메커니즘에 대해 자세히 설명합니다.
그림 2에 나타난 바와 같이, 메커니즘은 세 가지 구성 요소로 구성되어 있습니다: depth supervision, Elongation 필터 및 Decomposed-Gradient-based Densification (DGD).
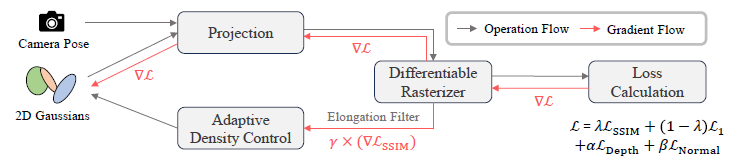
그림 2에 나타난 바와 같이, 2D 가우시안은 주어진 카메라 포즈로 화면 공간에 투사되고 맞춤형 래스터라이저에 의해 렌더링됩니다.
도출된 출력은 loss 계산에 사용됩니다.
GS 알고리즘은 각 뷰에서 단안 신호를 명확히 하기 위해 반복적인 최적화를 필요로 하며, 궁극적으로 일관된 3D 지오메트리로 수렴합니다.
수렴을 촉진하기 위해 지오메트리 최적화를 위한 보조 지침으로 depth prior를 통합합니다.
Kerbl et al. (2024)의 연습에 따라, 우리는 Depth-Anything-V2를 사용하여 인버스 depth를 추정하고 이를 데이터셋의 스케일 D_k에 맞추어 정렬합니다.
ˆD_k가 예측된 인버스 depth를 나타낸다고 가정해 보겠습니다.
관련 loss 함수는 L_Depth = |ˆD_k - D_k|로 정의됩니다.
학습이 진행됨에 따라 불완전한 depth 추정의 부작용을 점진적으로 억제하기 위해 loss 가중치 α를 지수적으로 줄입니다.
섹션 1에서 논의한 바와 같이, 2DGS를 확장하는 데 있어 중요한 장애물은 병렬 튜닝 단계에서 특정 프리미티브가 과도하게 증식하는 것입니다.
일반적으로 2D 가우시안은 먼 거리에서 투영될 때 매우 작은 지점까지 붕괴될 수 있으며, 특히 극도의 elongation을 보이는 가우시안은 매우 작은 지점까지 붕괴될 수 있습니다 (Huang et al., 2024).
불투명도가 높으면 이러한 미세한 점들의 움직임이 복잡한 장면에서 상당한 픽셀 변화를 일으켜 뚜렷한 위치 그래디언트를 초래할 수 있습니다.
그림 3의 왼쪽 부분에서 알 수 있듯이, 이 작은 모래 모양의 투영된 점들은 높은 그래디언트를 가진 점들에 크게 기여합니다.
그리고 그들은 극도로 elongation에 속합니다.
게다가, 일부 점들은 한 픽셀보다 작게 투사되어, 그 공분산이 안티앨리어스 저역 통과 필터를 통해 고정된 값으로 대체됩니다.
따라서 이러한 점들은 유효한 그래디언트로 스케일링과 회전을 적절히 조정할 수 없습니다.
블록 단위 병렬 튜닝에서는 각 블록에 할당된 뷰가 전체 뷰보다 훨씬 적습니다.
따라서 이러한 원거리 뷰가 자주 관찰되어 퇴화된 점들의 그래디언트가 빠르게 축적됩니다.
이러한 점들은 결과적으로 가우시안 수의 기하급수적인 증가를 유발하고, 궁극적으로 그림 3의 오른쪽 부분에서 보여지듯이 메모리 부족 오류를 초래합니다.
이 관찰을 바탕으로, 우리는 이 문제를 해결하기 위해 간단하면서도 효과적인 Elongation 필터를 구현합니다.
밀도화 전에 각 surfel의 elongation율을 평가합니다, 이는 η_n = min(s_(n,u), s_(n,v)) / max(s_(n,u), s_(n,v))로 정의됩니다.
η_n이 특정 임계값 이하인 surfel은 복제 및 분할 과정에서 제외됩니다.
그림 3의 오른쪽 부분에서 볼 수 있듯이, 이 필터는 메모리 부족 오류를 완화하고 보다 안정적인 가우시안 카운트 진화를 촉진합니다.
또한, 표 2의 실험 결과는 사전 학습 단계에서 성능을 저하시키지 않는다는 것을 보여줍니다.

나이브 2DGS는 대규모 장면으로 이동할 때 최적화되지 않는 문제를 겪기도 합니다.
우리는 실험적으로 2DGS가 초기 학습 단계에서 3DGS보다 블러 재구성에 더 취약하다는 것을 발견했습니다, 이는 부록의 그림 10에 나와 있습니다.
Wang et al. (2004), Zhang et al. (2024b), Shi et al. (2024)이 지적한 바와 같이, SSIM loss와 달리 L1 RGB loss는 블러에 민감하지 않으며 구조적 무결성을 보존하는 데 우선순위를 두지 않습니다.
부록의 표 6은 적응 밀도 제어의 그래디언트 소스에 대해 추가로 설명하며, 그래디언트의 참여가 최적이 아닌 결과에 가장 중요하다는 것을 확인합니다.
이 문제를 완화하기 위해 SSIM loss의 그래디언트를 우선시하고 Decomposed-Gradient-based Densification (DGD) 전략을 도입합니다.
구체적으로, 밀도화를 위한 그래디언트는
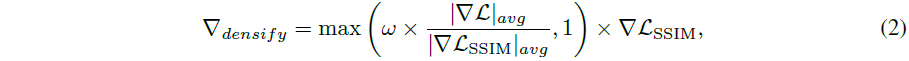
로 재구성되며, 여기서 ∇L_SSIM은 총 loss의 평균 그래디언트 노름에 따라 스케일링되어 밀도화를 위한 원래의 그래디언트 임계값과 자동으로 정렬되며, ω은 일정한 가중치를 나타냅니다.
3.3 Parallel Training Pipeline
섹션 1에서 논의한 바와 같이, CityGaussian의 포스트-프루닝 및 distillation은 시간이 많이 걸립니다.
병렬 튜닝 중에 상당한 메모리 오버헤드가 발생합니다.
이러한 문제들을 고려하여, 우리는 그림 4와 같은 새로운 파이프라인을 제안합니다.
distillation 단계를 우회하기 위해 처음부터 SH 도수를 2로 사용하여 SH 피쳐 차원을 48에서 27로 줄였습니다.
이로 인해 파이프라인 전체에 걸쳐 상당한 메모리 및 스토리지 절약이 이루어집니다.
포스트-프루닝의 필요성을 없애기 위해 블록 단위 튜닝 시 트리밍을 통합합니다.
구체적으로, Fan et al. (2024)에 이어 각 가우시안의 단일 뷰 기여도를 정의합니다:
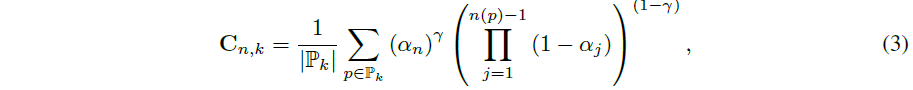
, 여기서 P_k는 k번째 뷰에서 n번째 가우시안의 2D 투영 영역입니다.
n(p)는 ray 교차 픽셀 p에서 depth 정렬된 순서를 나타냅니다.
γ은 기본값 0.5로 설정되어 있습니다.
CityGS (Liu et al., 2024)의 전략을 사용하여 m번째 블록에 할당된 이미지가 V_m이라고 가정하면 평균 기여도는
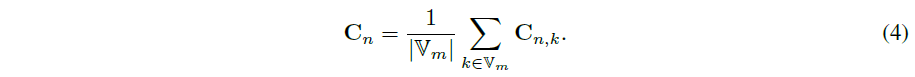
입니다.
이 기여는 학습 시작 시와 미리 정의된 시기 간격으로 평가됩니다.
우리의 접근 방식은 백분위수 기반 임계값을 사용하여 어떤 지점을 버릴지 결정한다는 점에서 Fan et al. (2024)과 다릅니다.
이 한도 이하의 기여도를 가진 포인트는 중복되거나 관찰되지 않은 포인트를 포함하여 자동으로 제거됩니다.
표 2는 우리 파이프라인이 50%의 저장 공간과 40%의 메모리를 절약하는 동시에 시간 비용을 줄이고 성능을 약간 향상시킨다는 것을 확인합니다.
다양한 블록에 걸쳐 가우시안을 병합한 후, 2DGS에서 벡터 양자화를 구현합니다.
먼저 모든 학습 데이터에 대한 각 포인트의 기여도를 평가합니다.
가장 중요하지 않은 가우시안은 SH에서 공격적인 벡터 양자화를 겪습니다.
나머지 임계 SH와 가우시안 형태, 회전, 불투명도를 나타내는 다른 속성들은 float16 형식으로 저장됩니다.
4 Geometric evaluation protocols
렌더링 품질 평가 프로토콜은 잘 확립되어 있으며 전송이 가능합니다.
우리는 렌더링과 ground truth 간의 SSIM, PSNR, LPIPS를 측정하여 표준 관행을 준수합니다.
그러나 대규모 장면 재구성에서 기하학적 정확성을 평가하기 위한 보편적으로 받아들여지는 프로토콜은 아직 없습니다.
최근 GauU-Scene (Xiong et al., 2024)은 첫 번째 벤치마크를 도입했지만, 평가 프로토콜이 경계 효과를 간과하여 신뢰할 수 없는 평가를 초래했습니다.
예를 들어, 자체 논문 (Xiong et al., 2024)에서 언급된 바와 같이, 이러한 프로토콜은 SuGaR의 기하학적 정확도를 크게 과소평가하여 메시 시각화에서 유망한 성능을 보여줍니다.
게다가 GauU-Scene은 표면 포인트 추출 과정을 여러 방법으로 정렬하지 않아 불공정한 비교를 초래합니다.
특히 NeRF 기반 방법은 depth 맵에서 포인트를 추출하는 반면, 3DGS는 가우시안 평균을 활용합니다.
이러한 문제를 해결하기 위해 우리는 포인트 클라우드 정렬, 리샘플링, 볼륨 제한 자르기, F1-score 측정을 포함하는 Tanks and Temple (TnT) 데이터셋 (Knapitsch et al., 2017)의 평가 프로토콜에서 교훈을 얻습니다.
모든 비교 방법에 대해 먼저 메쉬를 추출한 다음 표면에서 포인트를 샘플링합니다.
TnT의 정점과 면 중심을 샘플링하는 전략은 빠르지만, 큰 삼각형을 잘못 배치하는 효과를 과소평가할 수 있습니다.
따라서 표면에 동일한 수의 점을 고르게 샘플링합니다.

경계 효과 문제를 더 해결하기 위해서는 크롭의 양을 적절히 추정하는 것이 필요합니다.
여기서 핵심은 각 점의 가시 주파수를 확인하고 드물게 관찰되는 점을 제외할 수 있는 경계를 추정하는 것입니다.
효율성을 위해, 우리는 포인트를 가우시안 프리미티브로 공식화하고 잘 최적화된 GS 래스터라이저를 사용하여 그 가시성을 확인하는 해결책을 취합니다.
그림 5에 나타난 바와 같이, 우리는 ground truth 포인트 클라우드를 사용하여 3DGS 필드를 초기화한 다음, 모든 학습 뷰를 탐색하여 출력 가시 마스크를 통해 가시 주파수를 래스터화하고 계산합니다.
j번째 점 τ_j의 빈도가 미리 정의된 임계값 이하인 경우 제외됩니다.
남은 점들은 지면에서 알파 모양뿐만 아니라 최소 높이와 최대 높이를 계산하는 데 사용됩니다.
이 과정은 1분 이내에 완료할 수 있습니다.
모든 지점에서 추정된 크롭 양과 비교했을 때, 우리는 F1 score의 오차 막대 길이를 0.1에서 0.003으로 줄여 모델의 실제 성능을 안정적이고 일관적이며 신뢰할 수 있는 평가를 가능하게 합니다.
자동 크롭 생산량 추정 외에도, 우리는 대규모 장면에서 평가 과정을 가속화하기 위해 실제 포인트 클라우드를 다운샘플링합니다.
다운샘플링 복셀 크기는 0.35m로 설정됩니다.
다운샘플링된 ground truth 포인트 클라우드에서 가장 가까운 이웃 거리의 통계에 따르면 τ의 거리 임계값은 0.3m에서 0.6m까지 다양합니다.
5 Experiments
5.1 Experimental Setup
Datasets.
정확한 ground-truth 포인트 클라우드가 포함된 데이터셋이 필요합니다.
따라서 우리는 현실적인 데이터셋 GauU-Scene (Xiong et al., 2024)과 합성 데이터셋 MatrixCity (Li et al., 2023a)를 활용합니다.
GauU-Scene에서 Residence, Russian Building, 및 Modern Building 장면을 선택했습니다.
MatrixCity의 경우, 항공 뷰와 스트리트 뷰 버전에 대해 각각 실험을 진행합니다.
각 장면은 4,000개 이상의 학습 이미지와 450개 이상의 테스트 이미지로 구성되어 있어 상당한 어려움을 겪고 있습니다.
이 다섯 장면은 0.3km²에서 2.7km² 범위에 걸쳐 있습니다.
항공 뷰의 경우, Kerbl et al. (2023)을 따라 이미지의 긴 측면을 1,600픽셀로 다운샘플링합니다.
스트리트 뷰의 경우, 원래의 1,000 × 1,000 해상도를 유지합니다.
초기 희소 포인트 클라우드를 생성하기 위해 제공된 포즈와 함께 COLMAP (Sch ¨onberger & Frahm, 2016; Sch ¨onberger et al., 2016)을 사용합니다.
ground truth 포인트 클라우드는 기하학적 평가에만 사용됩니다.
Implementation Details.
우리의 실험은 8개의 A100 GPU에서 수행되었습니다.
우리는 그래디언트 스케일링 계수 ω을 0.9로 설정하고 프루닝 비율을 0.025로 설정했습니다.
depth 왜곡 loss의 경우, 성능에 해롭다는 것을 경험적으로 발견하여 가중치를 기본값 0으로 설정했습니다.
L_Depth의 가중치는 사전 학습 및 파인튜닝 단계 모두에서 0.5에서 0.0025로 지수적으로 감소합니다.
L_Normal은 사전 학습 시 7,000번의 반복 후에 활성화되며, 병렬 튜닝 시 처음부터 활성화됩니다.
게다가, 복잡한 장면 재구성을 위해 원래의 노멀 supervision이 지나치게 공격적이라는 것을 발견했습니다.
결과적으로, L_Normal의 무게는 원래 값의 4분의 1인 0.0125로 줄어듭니다.
우리는 학습 속도와 밀도화 일정에 대해 CityGaussian (Liu et al., 2024)의 기본 설정을 준수합니다.
구체적으로 말하자면, 튜닝 중 학습률이 관련된 경우에 비해 낮으며, 스트리트 뷰는 극단적인 뷰 희소성으로 인해 학습률이 현저히 낮고 밀도 간격이 길어집니다(Zhou et al., 2024).
페이지 제한으로 인해 블록 분할 및 양자화 매개변수를 포함한 추가 세부 정보가 부록에 제공됩니다.
depth 렌더링을 위해 중앙 depth를 활용하여 기하학적 정확도를 향상시키고, 메쉬 추출을 위해 복셀 크기가 1m이고 SDF 절단이 4m인 2DGS의 TSDF 기반 알고리즘을 사용합니다.
또한 GauU-Scene은 depth 절단 250m를 적용하고, MatrixCity는 500m를 사용합니다.
Baselines.
우리는 우리의 방법을 표면 재구성을 위한 SOTA 가우시안 스플래팅 방법들과 비교합니다, 여기에는 SuGaR (Gu'edon & Lepetit, 2024), 2DGS (Huang et al., 2024), GOF (Yu et al., 2024c)가 포함됩니다.
NeuS (Wang et al., 2021) 및 Neuralangelo (Li et al., 2023b)와 같은 암시적 NeRF 기반 방법도 포함되어 있습니다.
공정한 비교를 위해 Lin et al. (2024); Liu et al. (2024)을 따라 전체 반복 횟수를 두 배로 늘립니다; GS 기반 또는 NeRF 기반 방법의 예열 및 어닐링 반복에 대한 시작 반복과 밀도화 간격도 두 배로 늘어납니다.
GOF의 메쉬 추출은 1G를 초과하는 매우 고해상도의 메쉬를 생성하며, 이는 SuGaR 및 2DGS의 원래 설정에서 생성된 메쉬보다 훨씬 더 큰 것을 관찰했습니다.
공정성을 보장하기 위해 이러한 방법의 메쉬 추출 매개변수를 조정하여 해상도를 조정했습니다.
대규모 장면 재구성을 위해, 제출 당시 다른 동시 항공 뷰 기반 방법들은 오픈 소스가 아니었기 때문에, 우리는 CityGaussian (Liu et al., 2024)을 대표로 사용합니다.
메쉬 추출을 위해 2DGS의 방법론을 채택하고 TSDF 통합을 위해 중앙값 depth를 사용합니다.
5.2 Comparison with SOTA methods
이 섹션에서는 CityGaussianV2를 정량적 및 정성적으로 SOTA 방법과 비교합니다.
표 1에서 볼 수 있듯이, NeRF 기반 방법은 대규모 장면에서 MLP의 NaN 출력이나 희박한 supervision 하에서의 낮은 수렴으로 인해 실패할 가능성이 더 높습니다.
게다가, 이러한 방법들은 일반적으로 학습하는 데 10시간 이상 걸립니다.
반면, GS 기반 방법은 몇 시간 내에 학습을 완료하면서 더 강력한 성능과 일반화 능력을 보여줍니다.
GauU-Scene의 경우, 우리 모델은 렌더링 품질 면에서 기존의 기하학적 특화 방법을 크게 능가합니다.
그림 7에 시각적으로 나타낸 바와 같이, 우리의 방법은 혼잡한 창문과 숲과 같은 세부 사항을 정확하게 재구성합니다.
기하학적으로 우리 모델은 2DGS보다 0.01 F1 score 더 우수합니다.
또한, 그림 1의 (b) 부분은 병렬 튜닝 없이도 제안된 최적화 전략이 우리 모델이 7K와 30K 반복 모두에서 렌더링과 지오메트리에서 훨씬 더 나은 성능을 달성할 수 있게 해주는 반면, 2DGS는 크고 블러 surfels을 효율적으로 최적화하는 데 어려움을 겪고 있음을 보여줍니다.
이는 수렴 속도에서 우리의 우월성을 입증합니다.
CityGS와 비교했을 때, 우리의 방법은 PSNR에서 최소한의 차이를 유지하면서 F1 score를 0.1만큼 향상시킵니다.
그림 6에서 검증된 바와 같이, 우리 방법으로 생성된 메쉬는 더 부드럽고 완전합니다.

도전적인 MatrixCity 데이터셋에서 우리는 항공 뷰와 스트리트 뷰 모두에서 성능을 평가합니다.
MatrixCity-Aerial의 경우, 우리의 방법은 모든 알고리즘 중에서 최고의 표면 품질을 달성하며, F1 score는 2DGS의 두 배에 달하며 CityGaussian을 큰 차이로 능가합니다.
게다가 SuGaR과 GOF는 모두 학습을 완료하거나 의미 있는 메시를 추출하는 데 실패합니다.
스트리트 뷰에서 보면, CityGS와 2DGS와 같은 기하학적 특화 방법들은 기하학적으로 우리의 방법을 크게 능가하지 못합니다.
부록의 그림 9에 나타난 바와 같이, 우리의 방법은 도로 및 건물 표면의 질적으로 더 나은 재구성을 제공하며, CityGS에 필적하는 렌더링 품질을 제공합니다.

학습 비용과 관련하여, 표 2에 나와 있듯이, CityGaussianV2의 작은 버전은 학습 시간을 25% 줄이고 메모리 사용량을 50% 이상 줄이면서 CityGS와 함께 뛰어난 기하학적 성능과 동등한 렌더링 품질을 제공합니다.
작은 버전 (ours-t)은 학습 시간을 절반으로 줄일 수도 있습니다.
이러한 장점들은 우리의 방법을 다양한 품질과 즉각성 요구 사항을 가진 시나리오에 특히 적합하게 만듭니다.
5.3 Ablation Studies
이 섹션에서는 모델 디자인의 각 구성 요소를 요약합니다.
표 2의 상단 부분은 최적화 메커니즘에 중점을 둡니다.
보시다시피, 고도로 길쭉한 가우시안의 밀도를 제한하는 것은 사전 학습 성능에 미치는 영향이 미미합니다.
그러나 그림 3에서 볼 수 있듯이, 이 전략은 파인튜닝 단계에서 가우시안 카운트 폭발을 방지하는 데 필수적입니다.
또한, 표 2는 우리의 Decomposed Densification Gradient (DGD) 전략이 수렴을 크게 가속화하여 1.0 PSNR, 0.04 SSIM, 그리고 거의 0.02 F1 score를 향상시킨다는 것을 보여줍니다.
다양한 loss로부터의 그래디언트가 성과에 미치는 영향에 대한 보다 자세한 분석은 부록에 포함되어 있습니다.
상단 섹션의 마지막 두 줄은 Depth-Anything-V2 (Yang et al., 2024)의 depth supervision이 기하학적 품질을 상당히 향상시킨다는 것을 확인합니다.
표 2의 하단 부분에서는 파이프라인 설계를 살펴봅니다.
병렬 튜닝을 통해 렌더링과 지오메트리 품질이 크게 향상되어 확장의 성공을 입증했습니다.
트리밍을 위해, 우리는 0.1의 더 공격적인 프루닝 비율을 사용하여 저장 공간과 메모리를 50% 줄였습니다.
이 결과는 또한 실시간 성능을 위한 트리밍의 중요성을 강조합니다, 그러나 LightGaussian의 (Fan et al., 2023) 프루닝 전략은 렌더링 품질을 유지하는 데 부족합니다.
SH 도수 2를 처음부터 사용함으로써 저장 및 메모리 사용량을 25% 이상 줄이면서 렌더링 성능이나 지오메트리 정확도에 미치는 영향은 미미합니다.
속도가 4.2FPS 향상되었습니다.
기여도 기반 벡터 양자화 단계는 압축에 몇 분이 걸리지만 저장 공간을 75% 줄였습니다.
또한, 7,000번의 반복 결과를 사전 학습으로 사용하면 총 학습 시간이 3시간에서 2시간으로 단축되며, 모델 크기는 300MB 이하로 줄어듭니다.
이 컴팩트 모델은 스마트폰이나 VR 헤드셋과 같은 저가형 기기에 배포하기에 적합합니다.
그러나 블록 파티션을 7,000번의 2DGS 반복에서 생성된 것으로 대체하면 PSNR과 F1 score가 크게 떨어집니다.
이 최적이 아닌 결과는 작은 모델의 효율적인 학습을 위해 빠른 수렴의 중요성을 강조합니다.
6 Concusion
이 논문에서는 GS 기반 표면 재구성 방법의 확장 과제를 밝히고, 대규모 장면에 대한 기하학적 벤치마크를 확립합니다.
우리의 CityGaussianV2는 2DGS를 기본값으로 사용하여 수렴 속도와 확장 기능에서 문제를 제거합니다.
그럼에도 불구하고, 우리는 2DGS를 위한 병렬 학습과 압축도 구현하여 CityGaussian에 비해 상당히 낮은 학습 비용을 실현합니다.
여러 도전적인 데이터셋에 대한 실험 결과는 우리 방법의 효율성, 효과성 및 견고성을 입증합니다.