2022. 12. 29. 17:00ㆍDiffusion
Denoising Diffusion Probabilistic Models
Jonathan Ho, Ajay Jain, Pieter Abbeel
Abstract
우리는 비평형 열역학의 고려 사항에서 영감을 받은 잠재 변수 모델의 클래스인 diffusion 확률 모델을 사용하여 고품질 이미지 합성 결과를 제시한다.
우리의 최상의 결과는 diffusion 확률 모델과 Langevin dynamics와의 denoising score matching 사이의 새로운 연결에 따라 설계된 가중 변동 경계에 대한 학습을 통해 얻어지며, 우리의 모델은 자연스럽게 자기 회귀 디코딩의 일반화로 해석될 수 있는 점진적 lossy 압축 체계를 인정한다.
무조건적 CIFAR10 데이터 세트에서 Inception score 9.46과 SOTA FID score 3.17을 얻는다.
256x256 LSUN에서는 Progressive GAN과 유사한 샘플 품질을 얻습니다.
1 Introduction
모든 종류의 심층 생성 모델은 최근 다양한 데이터 양식에서 고품질 샘플을 보여주었다.
generative adversarial networks (GAN), autoregressive 모델, flows 및 variational autoencoders (VAE)는 눈에 띄는 이미지 및 오디오 샘플[14, 27, 3, 58, 38, 25, 10, 32, 44, 57, 26, 33, 45]을 합성했으며, GAN과 비슷한 이미지를 생성한 에너지 기반 모델링 및 score matching에서 괄목할 만한 발전이 있었다 [11, 55].

이 논문은 diffusion 확률 모델의 진전을 제시한다[53].
diffusion 확률 모델(이를 간결성을 위해 우리는 "diffusion model"이라고 부를 것입니다)은 유한 시간 후에 데이터와 일치하는 샘플을 생성하기 위해 변형 추론을 사용하여 학습된 매개 변수화된 마르코프 체인이다.
이 체인의 transition은 신호가 파괴될 때까지 샘플링 반대 방향으로 데이터에 노이즈를 점진적으로 추가하는 마르코프 체인인 diffusion 프로세스를 reverse시키는 것으로 학습된다.
diffusion이 적은 양의 가우시안 노이즈로 구성될 경우 샘플링 체인 transition을 조건적 가우시안으로 설정하면 충분하므로 특히 간단한 신경망 매개 변수화가 가능하다.

diffusion 모델은 정의하기 쉽고 학습하기에 효율적이지만, 우리가 아는 한 고품질 샘플을 생성할 수 있다는 것은 입증되지 않았다.
우리는 diffusion 모델이 실제로 고품질 샘플을 생성할 수 있으며, 때로는 다른 유형의 생성 모델에 대한 발표된 결과보다 더 낫다는 것을 보여준다(섹션 4).
또한, 우리는 diffusion 모델의 특정 매개 변수화가 학습 중 여러 노이즈 레벨에 걸쳐 일치하는 denoising score와 샘플링 중 Annealed Langevin dynamics와의 동등성을 보여준다는 것을 보여준다(섹션 3.2) [55, 61].
이 매개 변수화(섹션 4.2)를 사용하여 최상의 샘플 품질 결과를 얻었기 때문에 이 동등성을 주요 기여 중 하나로 간주한다.
샘플 품질에도 불구하고, 우리의 모델은 다른 likelihood 기반 모델과 비교하여 경쟁력 있는 log likelihood를 가지고 있지 않다(그러나, 우리의 모델은 에너지 기반 모델과 score matching에 대해 annealed importance sampling이 생성했다고 보고된 큰 추정치보다 log likelihood가 더 높다[11,55]).
우리는 모델의 lossless 코드 길이의 대부분이 감지할 수 없는 이미지 세부 정보를 설명하는 데 사용된다는 것을 발견했다(섹션 4.3).
우리는 lossy 압축의 언어로 이 현상에 대한 보다 정교한 분석을 제시하고, diffusion 모델의 샘플링 절차가 일반적으로 autoregressive 모델로 가능한 것을 크게 일반화하는 비트 순서를 따라 autoregressive 디코딩과 유사한 일종의 점진적 디코딩임을 보여준다.
2 Background
diffusion 모델[53]은 p_θ(x_0) := ∫p(x_(0:T)) dx_(1:T), 여기서 x_1, ..., x_T는 데이터 x_0 ~ q(x_0)와 동일한 차원의 잠재입니다.
joint 분포 p_θ(x_(0:T)) reverse 프로세스라고 하며, 이 과정은 p(x_T) = N(x_T; 0, I)에서 시작하는 학습된 가우시안 transition을 갖는 마르코프 체인으로 정의된다:

diffusion 모델을 다른 유형의 잠재 변수 모델과 구별하는 것은 forward 프로세스 또는 diffusion 프로세스라고 불리는 대략적인 posterior q(x_(1:T)|x_0)가 분산 스케줄 β_1, ..., β_T에 따라 데이터에 가우시안 노이즈를 점진적으로 추가하는 마르코프 체인에 고정된다는 것이다:
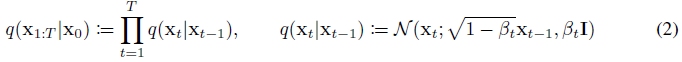
음의 log likelihood에 대한 일반적인 변동 경계를 최적화하여 학습을 수행합니다:

forward 프로세스 분산 β_t는 재매개 변수화[33]에 의해 학습되거나 하이퍼 파라미터로 일정하게 유지될 수 있으며, 두 프로세스 모두 t가 작을 때 동일한 함수 형태를 가지기 때문에 reverse 프로세스의 표현성은 부분적으로 p_θ(x_(t-1)|x_t)에서 가우시안 조건의 선택에 의해 보장된다[53].
forward 프로세스의 주목할 만한 특성은 닫힌 형태로 임의의 시간 단계 t에서 x_t를 샘플링할 수 있다는 것이다: α_t := 1 - β_t 및  ̄α_t := ∏ α_s 표기법을 사용하면

가 있다.
따라서 stochastic gradient descent로 L의 랜덤 항을 최적화함으로써 효율적인 학습이 가능하다.
또한 L (3)을

로 다시 작성하여 분산을 줄일 수 있습니다. (자세한 내용은 부록 A를 참조하십시오. 항의 라벨은 섹션 3에 사용됩니다.)
식 (5)은 KL divergence를 사용하여 p_θ(x_(t-1)|x_t)를 forward 프로세스 posteriors와 직접 비교하는데, 이는 x_0에서 조건화되었을 때 다루기 쉽다:

결과적으로, 식 (5)의 모든 KL divergence는 가우시안 사이의 비교이므로, 높은 분산 Monte Carlo 추정 대신 닫힌 형태 표현으로 Rao-Bloackwellized 방식으로 계산할 수 있다.
3 Diffusion models and denoising autoencoders
diffusion 모델은 잠재 변수 모델의 제한된 클래스로 보일 수 있지만, 구현에서 많은 자유도를 허용한다.
forward 프로세스의 분산 β_t와 reverse 프로세스의 모델 아키텍처 및 가우시안 분포 매개변수화를 선택해야 합니다.
우리의 선택을 안내하기 위해 diffusion 모델과 denoising score matching (섹션 3.2) 사이의 새로운 명시적 연결을 설정하여 diffusion 모델에 대한 단순화되고 가중된 변동 경계 목표(섹션 3.4)를 도출한다.
궁극적으로, 우리의 모델 설계는 단순성과 경험적 결과에 의해 정당화된다(섹션 4).
우리의 논의는 식 (5)의 항에 따라 분류된다.
3.1 Forward process and L_T
우리는 forward 프로세스 분산 β_t가 재매개 변수화에 의해 학습될 수 있다는 사실을 무시하고 대신 상수로 고정한다(자세한 내용은 섹션 4 참조).
따라서 우리의 구현에서 대략적인 posterior q는 학습 가능한 매개 변수가 없으므로 L_T는 학습 중 상수이므로 무시할 수 있다.
3.2 Reverse process and L_(1:T-1)
이제 우리는 1 < t ≤ T에 대한 p_θ(x_(t-1)|x_t) = N(x_(t-1); μ_θ(x_t, t), Σ_θ(x_t, t))에서 우리의 선택에 대해 논의한다.
먼저, 우리는 Σ_θ(x_t, t) = σ_t^2 I를 학습되지 않은 시간 의존 상수로 설정한다.
실험적으로 σ_t^2 = β_t와 σ_t^2 = ~β_t = (1 - ~α_(t-1))/(1 - ~α_t) β_t 모두 유사한 결과를 보였다.
첫 번째 선택은 x_0 ~ N(0, I)에 대해 최적이고, 두 번째 선택은 결정론적으로 한 점으로 설정된 x_0에 대해 최적입니다.
이것은 좌표 단위 분산이 있는 데이터에 대한 reverse 프로세스 엔트로피의 상한과 하한에 해당하는 두 가지 극단적인 선택입니다 [53].
둘째, 평균 μ_θ(x_t, t)를 나타내기 위해 다음과 같은 L_t 분석에 의해 동기 부여된 특정 매개 변수화를 제안한다.
p_θ(x_(t-1)|x_t) = N(x_(t-1);μ_θ(x_t, t), σ_t^2 I)로

을 쓸 수 있다, 여기서 C는 θ에 의존하지 않는 상수이다.
그래서 우리는 μ_θ의 가장 간단한 매개 변수화가 forward 프로세스 posterior 평균인 ~μ_t를 예측하는 모델이라는 것을 알 수 있다.
그러나, 우리는 식 (4)를 x_t(x_0, ε) = √( ̄α_t)x_0 + √(1- ̄α_t)ε for ε~N(0, I)로 다시 매개변수화하고 forward 프로세스 posterior 공식 (7)을 적용함으로써 식 (8)을 더 확장할 수 있다:

식 (10)은 x_t가 주어졌을 때 μ_θ가 1/√α_t(x_t - β_t/√(1-~α_t) ε)를 예측해야 한다는 것을 보여준다.
x_t는 모델에 대한 입력으로 사용할 수 있으므로 매개 변수화

를 선택할 수 있습니다, 여기서 ε_θ은 x_t에서 ε을 예측하기 위한 함수 근사치입니다.
x_(t-1) ~ p_θ(x_(t-1)|x_t)를 샘플링하는 것은 x_(t-1) = 1/√α_t (x_t - β_t/√(1-~α_t) ε_0(x_t, t))+σ_t z를 계산하는 것입니다. 여기서 z ~ N(0, I).
전체 샘플링 절차인 알고리즘 2는 데이터 밀도의 학습된 그레디언트로서 ε_θ을 가진 Langevin dynamics와 유사하다.
또한 매개변수화 (11)를 사용하면 식 (10)가

로 단순화되며, 이는 t [55]에 의해 인덱스된 여러 노이즈 스케일에 대한 denoising score matching과 유사하다.
식 (12)가 Langevin-like reverse 프로세스 (11)에 대한 변동 경계(의 한 항)와 같기 때문에 denoising score matching과 유사한 목표를 최적화하는 것은 Langevin dynamics와 유사한 샘플링 체인의 유한 시간 한계에 맞추기 위해 변동 추론을 사용하는 것과 동등하다는 것을 알 수 있다.

요약하자면, reverse 프로세스 평균 함수 근사치 μ_θ를 학습시켜 ~μ_t를 예측하거나 매개 변수화를 수정하여 ε을 예측할 수 있습니다. (x_0을 예측할 가능성도 있지만, 이는 실험 초기에 샘플 품질 저하로 이어진다는 것을 발견했습니다.)
우리는 ε-예측 매개 변수화가 Langevin dynamics와 유사하며 denoising score matching과 유사한 objective에 대한 diffusion 모델의 변형 경계를 단순화한다는 것을 보여주었다.
그럼에도 불구하고, 그것은 p_θ(x_(t-1)|x_t)의 또 다른 매개 변수화일 뿐이므로, 우리는 예측 ε과 ~μ_t를 비교하는 ablation에서 섹션 4에서 그 효과를 검증한다.
3.3 Data scaling, reverse process decoder, and L_0
이미지 데이터는 [-1, 1]까지 선형으로 스케일링된 {0, 1, ..., 255}의 정수로 구성된다고 가정한다.
이를 통해 신경망 reverse 프로세스가 표준 정상 prior p(x_T)에서 시작하여 일관되게 스케일링된 입력에서 작동하도록 보장한다.
이산 log likelihood를 얻기 위해, 우리는 reverse 프로세스의 마지막 항을 가우시안 N(x_0;μ(x_1, 1), σ_1^2 I)에서 파생된 독립적인 이산 디코더로 설정한다:
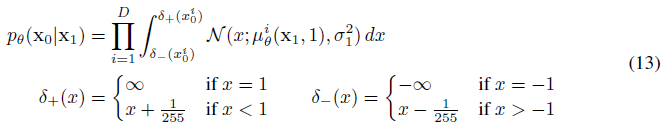
, 여기서 D는 데이터 차원이고 i superscript는 하나의 좌표의 추출을 나타냅니다. (대신 조건적 autoregressive 모델과 같은 더 강력한 디코더를 통합하는 것이 간단하겠지만, 우리는 그것을 향후 작업에 맡긴다.)
VAE 디코더 및 autoregressive 모델[34, 52]에 사용되는 이산화 연속 분포와 유사하게, 여기서 우리의 선택은 데이터에 노이즈를 추가하거나 스케일링 작업의 Jacobian을 log likelihood에 통합할 필요 없이 가변 경계가 이산 데이터의 lossless 코드 길이임을 보장한다.
샘플링이 끝나면 μ_θ(x_1, 1)를 노이즈 없이 표시합니다.
3.4 Simplified training objective
위에서 정의된 reverse 프로세스와 디코더로, 식 (12)와 (13)에서 파생된 항으로 구성된 변형 경계는 θ와 관련하여 명확하게 미분될 수 있으며 학습에 사용될 준비가 되어 있다.
그러나, 우리는 다음과 같은 변형된 변형 경계에 대해 학습하는 것이 샘플 품질(그리고 구현하기 더 간단함)에 유익하다는 것을 발견했다:

, 여기서 t는 1과 T 사이에서 균일하다.
t = 1 경우는 이산 디코더 정의(13)의 적분을 가진 L_0에 해당하며, 가우시안 확률 밀도 함수에 bin 폭을 곱하여 σ_1^2 및 에지 효과를 무시한다.
t > 1 사례는 가중치가 없는 버전의 식 (12)에 해당하며, NCSN denoising score matching 모델에 사용된 loss 가중치와 유사하다 [55]. (forward 프로세스 분산 β_t는 고정되어 있으므로 L_T는 나타나지 않습니다.)
알고리즘 1은 이 단순화된 objective로 전체 학습 절차를 표시한다.

우리의 단순화된 objective (14)는 식 (12)의 가중치를 무시하기 때문에, 표준 변동 경계와 비교하여 재구성의 다른 측면을 강조하는 가중 변동 경계이다[18, 22].
특히 섹션 4의 diffusion 프로세스 설정은 작은 t에 해당하는 loss 항을 낮추는 단순화된 objective를 야기한다.
이러한 항은 네트워크가 매우 적은 양의 노이즈로 데이터를 디노이즈하도록 학습하므로 네트워크가 더 큰 t 항으로 더 어려운 디노이즈 작업에 집중할 수 있도록 이를 줄이는 것이 유익하다.
우리는 실험에서 이러한 재조정이 더 나은 샘플 품질로 이어진다는 것을 알게 될 것이다.
4 Experiments
샘플링 중에 필요한 신경망 평가의 수가 이전 연구와 일치하도록 모든 실험에 대해 T=1000을 설정한다[53, 55].
우리는 forward 프로세스 분산을 β_1 = 10^-4에서 T= 0.02까지 선형적으로 증가하는 상수로 설정한다.
이러한 상수는 [-1, 1]로 스케일링된 데이터에 비해 작기로 선택되어 reverse 및 forward 프로세스가 거의 동일한 함수 형태를 가지면서 신호 대 잡음비를 가능한 한 작게 유지한다(L_T = D_KL (q(x_T|x_0) | N(0, I) ~ 10^-5 bits/dimension).
reverse 프로세스를 나타내기 위해 [66] 전체에 걸쳐 그룹 정규화가 있는 마스크되지 않은 PixelCNN++[52, 48]와 유사한 U-Net 백본을 사용한다.
매개변수는 시간에 걸쳐 공유되며, 이는 트랜스포머 사인파 위치 임베딩을 사용하여 네트워크에 지정된다[60].
우리는 16x16 피쳐 맵 해상도[63, 60]에서 셀프 어텐션을 사용한다.
자세한 내용은 부록 B에 있습니다.

4.1. Sample quality
표 1은 CIFAR10의 Inception score, FID score 및 음수 log likelihood (lossless 코드 길이)를 보여줍니다.
FID score가 3.17인 우리의 무조건적 모델은 클래스 조건적 모델을 포함한 문헌의 대부분 모델보다 더 나은 샘플 품질을 달성한다.
우리의 FID score는 표준 관행과 마찬가지로 학습 세트와 관련하여 계산된다.
테스트 세트와 관련하여 계산할 때 score는 5.24로 문헌에 나와 있는 많은 학습 세트 FID score보다 여전히 우수하다.
우리는 실제 변형 경계에 대한 모델 학습이 예상대로 단순화된 objective에 대한 학습보다 더 나은 코드 길이를 산출하지만, 후자는 최상의 샘플 품질을 산출한다는 것을 발견했다.
CIFAR10 및 CelebA-HQ 256x256 샘플의 경우 그림 1을, LSUN 256x256 샘플의 경우 그림 3 및 그림 4를, 자세한 내용은 부록 D를 참조하십시오.

4.2. Reverse process parameterization and training objective ablation
표 2에서는 reverse 프로세스 매개변수화 및 학습 objectives(섹션 3.2)의 샘플 품질 효과를 보여준다.
우리는 ~μ를 예측하는 베이스라인 옵션이 식 (14)와 유사한 단순화된 objective인 가중치가 없는 평균 제곱 오차 대신 실제 변동 한계에 대해 학습될 때만 잘 작동한다는 것을 발견했다.
우리는 또한 (파라미터화된 대각선 ∑_θ(x_t)를 변형 경계에 통합함으로써) reverse 프로세스 분산을 학습하면 고정 분산에 비해 학습이 불안정해지고 샘플 품질이 저하된다는 것을 알 수 있다.
우리가 제안한 바와 같이, ε을 예측하는 것은 고정된 분산을 가진 변동 경계에서 학습될 때 ~μ를 예측하는 것뿐만 아니라 대략적으로 수행되지만, 우리의 단순화된 objective로 학습될 때 훨씬 더 낫다.
4.3. Progressive coding
표 1은 CIFAR10 모델의 코드 길이도 보여줍니다.
학습과 테스트 사이의 간격은 차원당 최대 0.03비트이며, 이는 다른 likelihood 기반 모델과 함께 보고된 간격과 비슷하며 우리의 diffusion 모델이 과적합하지 않음을 나타낸다(가장 가까운 이웃 시각화는 부록 D 참조).
그럼에도 불구하고, 우리의 lossless 코드 길이는 annealed importance sampling을 사용하여 에너지 기반 모델과 score matching에 대해 보고된 큰 추정치[11]보다 낫지만, 다른 유형의 likelihood 기반 생성 모델과 경쟁력이 없다.
그럼에도 불구하고 우리의 샘플은 고품질이기 때문에, 우리는 diffusion 모델이 우수한 lossy 압축기를 만드는 유도 편향을 가지고 있다고 결론짓는다.
변동 경계 항 L_1 + ... + L_T을 비율로, L_0을 왜곡으로 처리하면 최고 품질의 샘플을 가진 CIFAR10 모델의 비율은 1.78 bits/dim이고 왜곡은 1.97 bits/dim이며, 이는 0에서 255까지의 척도에서 0.95의 평균 제곱 오차에 해당한다.
lossless 코드 길이의 절반 이상은 감지할 수 없는 왜곡을 설명한다.

Progressive lossy compression
우리는 식 (5)의 형태를 반영하는 점진적 loss 코드를 도입함으로써 우리 모델의 속도 왜곡 행동을 더 조사할 수 있다: p만 수신기가 미리 사용할 수 있는 모든 분포 p 및 q에 대해 평균적으로 약 D_KL(q(x)|p(x) 비트를 사용하여 샘플 x ~ q(x)를 전송할 수 있는 최소 랜덤 코딩 [19, 20]과 같은 절차에 대한 액세스를 가정하는 알고리즘 3 및 4를 참조하십시오.
x_0 ~ q(x_0)에 적용하면 알고리즘 3 및 4는 식 (5)와 동일한 총 예상 코드 길이를 사용하여 x_T, ..., x_0을 순차적으로 전송합니다.
수신기는 언제든지 부분 정보 x_t를 완전히 이용할 수 있으며 점진적으로 다음을 추정할 수 있다: (15) 식 (4) 때문에. (확률적 재구성 x_0 ~ p_θ(x_0|x_t)도 유효하지만, 왜곡을 평가하기 더 어렵게 만들기 때문에 여기서 고려하지 않는다.)
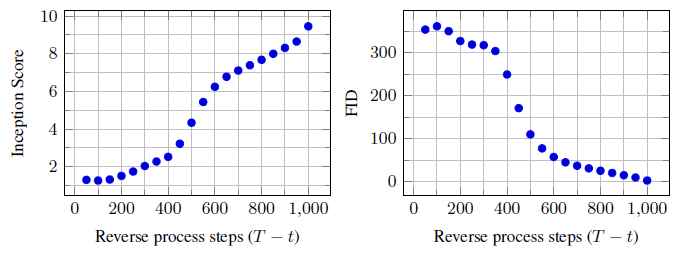
그림 5는 CIFAR10 테스트 세트의 결과 비율 왜곡 그림을 보여줍니다.
각 시간 t에서 왜곡은 근평균 제곱 오차 √(|x_0 - ^x_0|/D)로 계산되고, 속도는 시간 t에서 지금까지 수신된 누적 비트 수로 계산된다.
속도-왜곡 플롯의 낮은 비율 영역에서 왜곡이 가파르게 감소하며, 이는 대부분의 비트가 실제로 감지할 수 없는 왜곡에 할당되었음을 나타낸다.



Progressive generation
또한 랜덤 비트에서 점진적 압축 해제에 의해 주어진 점진적 무조건적 생성 프로세스를 실행한다.
즉, 알고리즘 2를 사용하여 reverse 프로세스에서 샘플링하면서 reverse 프로세스의 결과인 ^x_0을 예측한다.
그림 6과 10은 reverse 프로세스에서 ^x_0의 결과 샘플 품질을 보여줍니다.
대규모 이미지 피쳐가 먼저 나타나고 세부 정보가 마지막에 나타납니다.
그림 7은 다양한 t에 대해 x_t가 동결된 확률적 예측 x_0 ~ p_θ(x_0|x_t)를 보여준다.
t가 작으면 미세한 디테일을 제외한 모든 디테일이 보존되고, t가 크면 대규모 피쳐만 보존된다.
아마도 이것들은 개념적 압축의 힌트일 것이다 [18].

Connection to autoregressive decoding
변동 경계 (5)는

으로 다시 작성할 수 있음을 유의하십시오(추출은 부록 A 참조)
이제 diffusion 프로세스 길이 T를 데이터의 차원으로 설정하고, q(x_t|x_0)가 첫 번째 t 좌표를 마스크한 상태에서 모든 확률 질량을 x_0에 배치하도록 정의하고(즉, q(x_t|x_(t-1)) t번째 좌표를 마스크합니다.), p(x_T)가 모든 질량을 bin 이미지에 배치하도록 설정하고, 인수를 위해, p_θ(x_(t-1)|x_t)를 완전 표현형 조건 분포로 간주한다.
이러한 선택으로, D_KL(q(x_T)|p(x_T)) = 0이 되고, D_KL(q(x_(t-1)|x_t) | p_θ(x_(t-1)|x_t))를 최소화하면 p_θ가 좌표 t+1, ..., T를 변경하지 않고 t+1, ..., T가 주어진 좌표를 예측한다.
따라서 이 특정 diffusion으로 p_θ를 학습하는 것은 자기 회귀 모델을 학습하는 것이다.
따라서 우리는 가우시안 diffusion 모델 (2)을 데이터 좌표를 재정렬하여 표현할 수 없는 일반화된 비트 순서를 가진 일종의 자기 회귀 모델로 해석할 수 있다.
이전 연구에 따르면 이러한 재정렬은 샘플 품질에 영향을 미치는 귀납적 편향을 도입하는 것으로 나타났기 때문에 가우시안 diffusion이 유사한 목적에 도움이 될 것으로 추측한다[38].
가우시안 노이즈가 마스킹 노이즈에 비해 이미지에 추가하는 것이 더 자연스러울 수 있기 때문이다.
또한 가우시안 diffusion 길이는 데이터 차원과 동일하도록 제한되지 않는다; 예를 들어, 우리는 실험에서 32x32x3 또는 256x256x3 이미지의 차원보다 작은 T = 1000을 사용한다.
가우시안 diffusion은 빠른 샘플링을 위해 더 짧게, 모델 표현력을 위해 더 길게 만들 수 있다.

4.4 Interpolation
우리는 q를 확률적 인코더 x_t, x'_t ~ q(x_t|x_0)로 사용하여 잠재 공간에서 소스 이미지 x_0, x'_0 ~ q(x_0)를 보간한 다음, reverse 프로세스 x_0 ~ p(x_0|x_t)에 의해 선형 보간된 잠재 x_t = (1-λ)x_0 + λx'0을 이미지 공간으로 디코딩할 수 있다.
실제로, 우리는 그림 8(왼쪽)에 묘사된 것처럼 소스 이미지의 손상된 버전을 선형으로 보간하는 아티팩트를 제거하기 위해 reverse 프로세스를 사용한다.
우리는 x_t와 x'_t가 동일하게 유지되도록 λ의 다른 값에 대한 노이즈를 수정했다.
그림 8(오른쪽)은 원본 CelebA-HQ 256x256 이미지의 보간 및 재구성을 보여줍니다(t = 500).
reverse 프로세스는 고품질 재구성과 포즈, 피부톤, 헤어스타일, 표정, 배경 등의 속성을 부드럽게 변화시키는 그럴듯한 보간을 생성하지만 아이웨어는 생성하지 않는다.
t가 클수록 보간이 coarser하고 다양하며, 새로운 샘플은 t = 1000이다(부록 그림 9).

5 Related Work
diffusion 모델은 flows[9, 46, 10, 32, 5, 16, 23] 및 VAE[33, 47, 37]와 유사할 수 있지만, diffusion 모델은 q에 매개 변수가 없고 최상위 잠재 x_T에 데이터 x_0과의 상호 정보가 거의 없도록 설계된다.
우리의 ε-예측 reverse 프로세스 매개변수화는 샘플링을 위한 annealed Langevin dynamics를 사용하여 다중 노이즈 수준에 대한 diffusion 모델과 디노이징 score matching 사이의 연결을 설정한다[55, 56].
그러나 diffusion 모델은 간단한 log likelihood 평가를 허용하며, 학습 절차는 변동 추론을 사용하여 Langevin dynamics 샘플러를 명시적으로 학습시킨다(자세한 내용은 부록 C 참조).
이 연결은 또한 디노이징 score matching의 특정 가중 형태가 Langevin 유사 샘플러를 학습시키기 위한 변형 추론과 같다는 reverse의 의미를 갖는다.
마르코프 체인의 transition 연산자를 학습하기 위한 다른 방법으로는 주입 학습[2], 변형 워크백[15], 생성 확률적 네트워크[1], 기타[50, 54, 36, 42, 35, 65]가 있다.
score matching과 에너지 기반 모델링 사이의 알려진 연관성으로 인해, 우리의 연구는 에너지 기반 모델에 대한 다른 최근 연구에 영향을 미칠 수 있다[67–69, 12, 70, 13, 11, 41, 17, 8].
우리의 속도-왜곡 곡선은 변동 경계의 한 평가에서 시간이 지남에 따라 계산되며, 이는 어닐링된 중요도 샘플링의 한 번 실행에서 왜곡 페널티에 대해 속도-왜곡 곡선을 계산할 수 있는 방법을 연상시킨다[24].
우리의 점진적 디코딩 주장은 컨볼루션 DRAW와 관련 모델[18, 40]에서 볼 수 있으며, 또한 자기 회귀 모델에 대한 서브세일 주문 또는 샘플링 전략에 대한 더 일반적인 설계로 이어질 수 있다[38, 64].
6 Conclusion
우리는 diffusion 모델을 사용하여 고품질 이미지 샘플을 제시했고, 마르코프 체인을 학습하기 위한 diffusion 모델과 변형 추론, denoising score matching 및 소멸된 Langevin 역학(및 확장에 의한 에너지 기반 모델), autoregressive 모델 및 점진적 손실 압축 간의 연결을 발견했다.
diffusion 모델은 이미지 데이터에 대한 유도 편향이 우수한 것으로 보이기 때문에, 우리는 다른 데이터 양식과 다른 유형의 생성 모델 및 기계 학습 시스템의 구성 요소로서 그 유용성을 조사하기를 기대한다.