2023. 1. 9. 18:10ㆍDiffusion
Generative Modeling by Estimating Gradients of the Data Distribution
Yang Song, Stefano Ermon
Abstract
score matching으로 추정된 데이터 분포의 그레디언트를 사용하여 Langevin dynamics을 통해 샘플이 생성되는 새로운 생성 모델을 소개한다.
그레디언트는 데이터가 저차원 매니폴드에 상주할 때 잘못 정의되고 추정하기 어려울 수 있기 때문에, 우리는 다른 레벨의 가우시안 노이즈로 데이터를 섭동시키고 해당 score, 즉 모든 노이즈 레벨에 대한 섭동된 데이터 분포의 벡터 필드를 jointly 추정한다.
샘플링을 위해 샘플링 프로세스가 데이터 매니폴드에 가까워질수록 점차 감소하는 노이즈 레벨에 해당하는 그레디언트를 사용하는 annealed Langevin dynamics을 제안한다.
우리의 프레임워크는 유연한 모델 아키텍처를 허용하고, 학습 중에 샘플링하거나 적대적 방법을 사용할 필요가 없으며, 원칙적인 모델 비교에 사용할 수 있는 학습 objective를 제공한다.
우리 모델은 MNIST, CelebA 및 CIFAR-10 데이터 세트에서 GAN과 유사한 샘플을 생성하여 CIFAR-10에서 8.87의 새로운 SOTA inception score를 달성한다.
또한, 우리는 모델이 이미지 인페인팅 실험을 통해 효과적인 표현을 학습한다는 것을 보여준다.
1 Introduction
생성 모델은 머신러닝에 많은 응용 프로그램이 있다.
몇 가지 예를 들어, 그것들은 충실도가 높은 이미지 생성[26, 6], 사실적인 음성 및 음악 단편 합성[58], semi-supervised 학습의 성능 향상[28, 10], 적대적 사례 및 기타 변칙적 데이터 탐지[54], 모방 학습[22], 강화 학습의 유망한 상태 탐색에 사용되었다[41].
최근의 진전은 주로 두 가지 접근 방식에 의해 주도된다: likelihood 기반 방법[17, 29, 11, 60] 및 생성적 적대 네트워크(GAN [15]).
전자는 log-likelihood(또는 적절한 surrogate)를 학습 objective로 사용하는 반면, 후자는 적대적 학습을 사용하여 모델과 데이터 분포 사이의 f-divergence[40] 또는 적분 확률 메트릭[2,55]을 최소화한다.
likelihood 기반 모델과 GAN은 큰 성공을 거두었지만 본질적인 한계가 있다.
예를 들어, likelihood 기반 모델은 정규화된 확률 모델(예: autoregressive 모델, flow 모델)을 구축하기 위해 전문화된 아키텍처를 사용하거나 학습을 위해 surrogate losses(예: variational autoencoder에 사용되는 증거 하한, 에너지 기반 모델의 contrastive divergence [21])를 사용해야 한다.
GAN은 likelihood 기반 모델의 일부 제한을 피하지만 적대적 학습 절차로 인해 학습이 불안정할 수 있다.
또한 GAN objective는 다른 GAN 모델을 평가하고 비교하는 데 적합하지 않다.
noise contrastive estimation [19] 및 minimum probability flow [50]과 같은 생성 모델링에 대한 다른 objective가 존재하지만, 이러한 방법은 일반적으로 저차원 데이터에만 잘 작동한다.
본 논문에서는 입력 데이터 지점에서 로그 밀도 함수의 그래디언트인 로그 데이터 밀도의 (Stein) score[33]에서 추정 및 샘플링을 기반으로 생성 모델링을 위한 새로운 원칙을 탐구한다.
이것은 로그 데이터 밀도가 가장 많이 증가하는 방향을 가리키는 벡터 필드입니다.
우리는 score matching [24]으로 학습된 신경망을 사용하여 데이터에서 이 벡터 필드를 학습한다.
그런 다음 우리는 (추정된) score의 벡터 필드를 따라 랜덤 초기 샘플을 고밀도 영역으로 점진적으로 이동함으로써 대략적으로 작동하는 Langevin dynamics을 사용하여 샘플을 생산한다.
그러나 이 접근 방식에는 두 가지 주요 과제가 있다.
첫째, 데이터 분포가 많은 실제 데이터 세트에서 종종 가정되는 것처럼 저차원 매니폴드에서 지원되는 경우, score는 주변 공간에서 정의되지 않을 것이며, score matching은 일관된 score estimator를 제공하지 못할 것이다.
둘째, 매니폴드에서 멀리 떨어져 있는 등 데이터 밀도가 낮은 영역에서 학습 데이터의 희소성은 score estimation의 정확성을 저해하고 Langevin dynamics 샘플링의 혼합 속도를 늦춘다.
Langevin dynamics는 종종 데이터 분포의 저밀도 영역에서 초기화되기 때문에, 이러한 영역에서 부정확한 score matching은 샘플링 프로세스에 부정적인 영향을 미칠 것이다.
더욱이 분포 모드 간 전환을 위해 저밀도 영역을 횡단해야 하기 때문에 혼합이 어려울 수 있다.
이 두 가지 과제를 해결하기 위해 다양한 크기의 랜덤 가우시안 노이즈로 데이터를 섭동할 것을 제안한다.
랜덤 노이즈를 추가하면 결과 분포가 저차원 매니폴드로 붕괴되지 않습니다.
큰 노이즈 레벨은 원래(섭동되지 않은) 데이터 분포의 저밀도 영역에서 샘플을 생성하여 score estimation을 향상시킨다.
결정적으로, 우리는 노이즈 레벨에 따라 조정된 단일 score 네트워크를 학습하고 모든 노이즈 크기에서 score를 추정한다.
그런 다음 우리는 초기에 가장 높은 노이즈 레벨에 해당하는 score를 사용하고 원래 데이터 분포와 구별할 수 없을 정도로 작을 때까지 점차 노이즈 레벨을 어닐링하는 an annealed version of Langevin dynamics를 제안한다.
우리의 샘플링 전략은 멀티모달 풍경에 대한 최적화를 휴리스틱하게 개선하는 시뮬레이션 annealing [30, 37]에서 영감을 얻었다.
우리의 접근 방식에는 몇 가지 바람직한 특성이 있다.
첫째, 우리의 objective는 특별한 제약이나 아키텍처 없이 score 네트워크의 거의 모든 매개 변수화에 대해 추적 가능하며, 학습 중 적대적 학습, MCMC 샘플링 또는 기타 근사치 없이 최적화될 수 있다.
이 objective는 또한 동일한 데이터 세트에서 다른 모델을 정량적으로 비교하는 데 사용될 수 있다.
실험적으로, 우리는 MNIST, CelebA[34] 및 CIFAR-10[31]에 대한 접근 방식의 효과를 입증한다.
우리는 샘플이 현대의 likelihood 기반 모델 및 GAN에서 생성된 샘플과 비교할 수 있는 것처럼 보인다는 것을 보여준다.
CIFAR-10에서 우리 모델은 무조건적 생성 모델에 대한 새로운 SOTA inception score인 8.87을 설정하고 25.32의 경쟁력 있는 FID 점수를 달성한다.
우리는 모델이 이미지 인페인팅 실험을 통해 데이터의 의미 있는 표현을 학습한다는 것을 보여준다.
2 Score-based generative modeling
우리의 데이터세트가 알 수 없는 데이터 분포 p_data(x)의 i.i.d 샘플 {x_i ∈ R^D}_(i=1)^N으로 구성된다고 가정하자.
우리는 확률 밀도 p(x)의 score를 ∇_x log p(x)로 정의한다.
score 네트워크 s_θ : R^D → R^D는 θ에 의해 매개 변수화된 신경망으로, p_data(x)의 score를 근사하도록 학습될 것이다.
생성 모델링의 목표는 데이터세트를 사용하여 p_data(x)에서 새로운 샘플을 생성하기 위한 모델을 학습하는 것이다.
score 기반 생성 모델링의 프레임워크는 두 가지 요소로 구성된다: score matching과 Langevin dynamics.
2.1 Score matching for score estimation
score matching [24]은 원래 알려지지 않은 데이터 분포의 샘플을 기반으로 정규화되지 않은 통계 모델을 학습하기 위해 설계되었다.
[53]에 이어 score matching을 위해 용도를 변경한다.
score matching을 사용하여 먼저 p_data(x)를 추정하는 모델을 학습하지 않고도 ∇_x log p_data(x)를 추정하기 위해 score 네트워크 s_θ(x)를 직접 학습할 수 있다.
score matching의 일반적인 사용과 달리, 우리는 고차 그레디언트로 인한 추가 계산을 피하기 위해 에너지 기반 모델의 그레디언트를 score 네트워크로 사용하지 않기로 선택한다.
objective는 1/2 E_(p_data) [|s_θ(x) - ∇_x log p_data(x)|]를 최소화하는데, 이는 상수

까지 다음과 동등하게 나타낼 수 있다. 여기서 ∇_x s_θ(x)는 s_θ(x)의 Jacobian을 나타낸다.
[53]에 나온 것처럼, 일부 규칙성 조건에서 식 (3)(s_θ*(x))의 최소화기는 s_θ*(x) = ∇_x log p_data(x)를 거의 확실히 만족시킨다.
실제로, 식 (1)의 p_data(x)에 대한 기대치는 데이터 샘플을 사용하여 빠르게 추정할 수 있다.
그러나 score matching은 tr(∇_x s_θ(x))의 계산으로 인해 심층 네트워크 및 고차원 데이터[53]로 확장할 수 없다.
아래에서는 대규모 score matching을 위한 두 가지 인기 있는 방법에 대해 논의한다.
Denoising score matching.
denoising score matching [61]은 tr(∇_x s_θ(x))을 완전히 우회하는 score matching의 변형이다.
먼저 데이터 포인트 x를 사전 지정된 노이즈 분포 q_σ(~x|x)로 섭동한 다음 score matching을 사용하여 섭동된 데이터 분포 q_σ(~x)= ∫q_σ(~x|x) p_data(x) dx의 score를 추정한다.
그 objective는 다음

과 동등한 것으로 입증되었다.
[61]에 나타난 바와 같이, 식 (2)를 최소화하는 최적의 score 네트워크(s_θ*(x))는 s_θ*(x) = ∇_x log q_σ(x)를 거의 확실하게 만족시킨다.
그러나, s_θ* (x) = ∇_x log q_σ (x) = ∇_x log p_data (x)는 q_σ (x) = p_data (x)와 같이 노이즈가 충분히 작을 때만 참입니다.
Sliced score matching
Sliced score matching [53]는 랜덤 투영을 사용하여 score matching에서 tr(∇_x s_θ(x))를 근사한다.
objective는
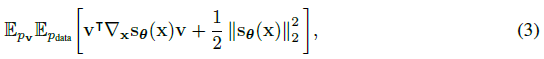
이며, 여기서 p_v는 다변량 표준 정규 분포와 같은 랜덤 벡터의 단순한 분포입니다.
[53]에 나타난 바와 같이, v^T ∇_x s_θ(x) v라는 항은 forward 모드 자동 미분에 의해 효율적으로 계산될 수 있다.
섭동 데이터의 score를 추정하는 denoising score matching과 달리 sliced score matching은 원래 섭동되지 않은 데이터 분포에 대한 score estimation을 제공하지만 forward 모드 자동 미분으로 인해 약 4배 더 많은 계산이 필요하다.
2.2 Sampling with Langevin dynamics
Langevin dynamics는 score 함수 ∇_x log p(x)만 사용하여 확률 밀도 p(x)에서 샘플을 생성할 수 있습니다.
고정된 단계 크기 ε > 0이고 π가 prior 분포인 초기 값 ~x_0 ~ π(x)가 주어지면, Langevin 방법은 다음

을 재귀적으로 계산한다, 여기서 z_t ~ N(0, I).
~x_T의 분포는 ε → 0과 T → ∞일 때 p(x)와 같으며, 이 경우 ~x_T는 일부 규칙성 조건에서 p(x)의 정확한 샘플이 된다[62].
ε > 0 및 T < ∞인 경우, 식 (4)의 오류를 수정하기 위해 Metropolis-Hastings 업데이트가 필요하지만, 실제로는 무시할 수 있는 경우가 많다[9, 12, 39].
이 작업에서, 우리는 ε가 작고 T가 클 때 이 오류가 무시할 수 있다고 가정한다.
식 (4)로부터의 샘플링에는 score 함수 ∇_x log p(x)만 필요합니다.
따라서 p_data(x)에서 샘플을 얻기 위해 먼저 s_θ(x) = ∇_x log p_data(x)와 같은 score 네트워크를 학습한 다음 s_θ(x)를 사용하여 Langevin dynamics를 가진 샘플을 대략적으로 얻을 수 있다.
이것은 score 기반 생성 모델링 프레임워크의 핵심 아이디어이다.
3 Challenges of score-based generative modeling
이 섹션에서는 score 기반 생성 모델링의 아이디어를 더 자세히 분석한다.
우리는 이 아이디어의 나이브한 적용을 막는 두 가지 주요 장애물이 있다고 주장한다.
3.1 The manifold hypothesis
매니폴드 가설은 실제 세계의 데이터가 고차원 공간(일명 주변 공간)에 내장된 저차원 매니폴드에 집중하는 경향이 있다고 말한다.
이 가설은 경험적으로 많은 데이터세트에 적용되며, 다양한 매니폴드 학습의 기초가 되었다[3, 47].
매니폴드 가설에 따르면 score 기반 생성 모델은 두 가지 주요 문제에 직면할 것이다.
첫째, score ∇_x log p_data(x)는 주변 공간에서 취해진 그래디언트이기 때문에, x가 저차원 매니폴드로 제한될 때 정의되지 않는다.
둘째, score matching objective 식 (1)는 데이터 분포의 지지가 전체 공간일 때만 일관된 score estimator를 제공하며([24]의 Theorem 2 참조), 데이터가 저차원 매니폴드에 상주할 때 일관성이 없다.

score estimation에 대한 매니폴드 가설의 부정적인 영향은 그림 1에서 명확하게 볼 수 있으며, 여기서 우리는 CIFAR-10의 데이터 score를 추정하기 위해 ResNet(부록 B.1의 세부 정보)을 학습한다.
빠른 학습과 데이터 score의 충실한 추정을 위해, 우리는 sliced score matching 목표를 사용한다(예: (3)).
그림 1(왼쪽)에서 알 수 있듯이, 원래 CIFAR-10 이미지에 대해 학습할 때 sliced score matching loss가 먼저 감소한 다음 불규칙하게 변동한다.
대조적으로, 작은 가우시안 노이즈로 데이터를 섭동하면(섭동된 데이터 분포가 R^D를 완전히 지원하도록) loss 곡선이 수렴된다(오른쪽 패널).
우리가 부과하는 가우시안 노이즈 N(0, 0.0001)은 픽셀 값이 [0, 1] 범위에 있는 이미지의 경우 매우 작으며 사람의 눈으로 거의 구별할 수 없습니다.
3.2 Low data density regions
저밀도 영역의 데이터 부족은 score matching을 통한 score estimation과 Langevin dynamics을 통한 MCMC 샘플링 모두에 어려움을 초래할 수 있다.
3.2.1 Inaccurate score estimation with score matching
데이터 밀도가 낮은 영역에서는 데이터 샘플이 부족하기 때문에 score matching이 score 함수를 정확하게 추정하기에 충분한 증거가 없을 수 있습니다.
이를 확인하려면 섹션 2.1에서 score matching이 score 추정치의 예상 제곱 오차를 최소화한다는 점을 상기하십시오, 즉, 1/2 E_(p_data) [|s_θ(x) - ∇_x log p_data(x)|].
실제로 데이터 분포와 관련된 기대치는 항상 i.i.d. 샘플 {x_i}_(i=1)^N ~ p_data(x)를 사용하여 추정된다.
p_data(R) = 0이 되도록 임의의 영역 R ⊂ R^D를 고려한다.
대부분의 경우 {x_i}_(i=1)^N ∩ R = Φ이며, score matching에는 x ∈ R에 대해 ∇_x log p_data(x)를 정확하게 추정하기에 충분한 데이터 샘플이 없습니다.

이것의 부정적인 영향을 입증하기 위해, 우리는 그림 2의 toy 실험(부록 B.1 참조)의 결과를 제공한다, 여기서 우리는 가우시안 p_data = 1/5N(-5,-5, I) + 4/5N((5,5, I)의 mixture의 score를 추정한다.
그림에서 알 수 있듯이, score estimation은 데이터 밀도가 높은 p_data 모드의 바로 근처에서만 신뢰할 수 있다.
3.2.2 Slow mixing of Langevin dynamics
데이터 분포의 두 모드가 저밀도 영역으로 분리되면 Langevin dynamics 는 이 두 모드의 상대적 가중치를 합리적인 시간 내에 올바르게 복구할 수 없으므로 실제 분포로 수렴하지 못할 수 있다.
이에 대한 우리의 분석은 주로 밀도 추정의 맥락에서 score matching으로 동일한 현상을 분석한 [63]에서 영감을 받았다.
mixture 분포 p_data(x) = π p_1(x)+(1-π)p_2(x)를 고려합니다, 여기서 p_1(x)과 p_2(x)는 분리된 지지대가 있는 정규화된 분포이고 π ∈ (0, 1)입니다.
p_1(x)을 지원하는 경우, ∇_x log p_data(x) = ∇_x(log π + log p_1(x)) = ∇_x log p_1(x), p_2(x)을 지원하는 경우, ∇_x log p_data(x) = ∇_x (log(1-π) + log p_2(x)) = ∇_x log p_2(x).
두 경우 모두 score ∇_x log p_data(x)는 π에 의존하지 않습니다.
Langevin dynamics는 p_data(x)에서 샘플을 추출하기 위해 ∇_x log p_data(x)를 사용하므로, 얻은 샘플은 π에 의존하지 않을 것이다.
실제로 이 분석은 서로 다른 모드가 대략적으로 분리된 지원을 가질 때에도 적용됩니다 - 이들은 동일한 지원을 공유할 수 있지만 데이터 밀도가 낮은 영역으로 연결됩니다.
이 경우, Langevin dynamics는 이론적으로 정확한 샘플을 만들 수 있지만, 혼합하기 위해서는 매우 작은 단계 크기와 매우 많은 단계가 필요할 수 있다.

이 분석을 검증하기 위해 섹션 3.2.1에 사용된 동일한 가우시안 mixture에 대한 Langevin dynamics 샘플링을 테스트하고 그 결과를 그림 3에 제공한다.
우리는 Langevin dynamics로 샘플링할 때 ground truth score를 사용한다.
그림 3(b)와 (a)를 비교하면, 우리의 분석에 의해 예측된 바와 같이 Langevin dynamics의 샘플이 두 모드 사이에 잘못된 상대 밀도를 가지고 있다는 것이 명백하다.
4 Noise Conditional Score Networks: learning and inference
우리는 랜덤 가우시안 노이즈로 데이터를 섭동하면 데이터 분포가 score 기반 생성 모델링에 더 적합하다는 것을 관찰한다.
첫째, 가우시안 노이즈 분포를 지원하는 것이 전체 공간이기 때문에 섭동된 데이터는 저차원 매니폴드에 국한되지 않으며, 이는 매니폴드 가설의 어려움을 제거하고 score estimation을 잘 정의하게 된다.
둘째, 큰 가우시안 노이즈는 원래 섭동되지 않는 데이터 분포에서 저밀도 영역을 채우는 효과가 있으므로 score matching은 score estimation을 개선하기 위해 더 많은 학습 신호를 얻을 수 있다.
또한, 여러 노이즈 레벨을 사용하여 실제 데이터 분포로 수렴하는 일련의 노이즈 섭동 분포를 얻을 수 있다.
우리는 simulated annealing [30]과 annealed importance sampling [37]의 정신으로 이러한 중간 분포를 활용하여 멀티모달 분포에 대한 Langevin dynamics의 혼합률을 개선할 수 있다.
이러한 직관을 바탕으로 1) 다양한 레벨의 노이즈를 사용하여 데이터를 섭동시키고, 2) 단일 conditional score 네트워크를 학습하여 모든 노이즈 레벨에 해당하는 score를 동시에 추정함으로써 score 기반 생성 모델링을 개선할 것을 제안한다.
학습 후, Langevin dynamics를 사용하여 샘플을 생성할 때, 우리는 처음에 큰 노이즈에 해당하는 score를 사용하고, 점차 score 레벨을 감소시킨다.
이는 섭동된 데이터가 원래의 것과 거의 구별할 수 없는 낮은 노이즈 레벨로 큰 노이즈 레벨의 이점을 원활하게 전달하는 데 도움이 된다.
다음에서, 우리는 score 네트워크의 아키텍처, 학습 objective, Langevin dynamics에 대한 annealing 스케줄을 포함한 우리 방법의 세부 사항에 대해 더 자세히 설명할 것이다.
4.1 Noise Conditional Score Networks
{σ_i}_(i=1)^L을 σ_1 / σ_2 = ... = σ_(L-1) / σ_L > 1을 만족하는 양의 기하학적 수열이라고 하자.
q_σ(x) = ∫p_data(t) N(x|t, σ^2 I)dt가 섭동된 데이터 분포를 나타낸다고 하자.
우리는 σ_1이 섹션 3에서 논의된 어려움을 완화할 수 있을 만큼 충분히 크고 σ_L이 데이터에 미치는 영향을 최소화할 수 있을 만큼 충분히 작도록 노이즈 레벨 {σ_i}_(i=1)^N을 선택한다.
우리는 섭동된 모든 데이터 분포의 score를 jointly 추정하기 위해 conditional score 네트워크를 학습하는 것을 목표로 한다, 즉, ∀σ ∈ {σ_i}_(i=1)^L : s_θ(x, σ) = ∇_x log q_σ(x).
x ∈ R^D일 때 s_θ(x, σ) ∈ R^D라는 점에 유의하십시오.
우리는 s_θ(x, σ)를 Noise Conditional Score Network (NCSN)이라고 부른다.
likelihood 기반 생성 모델 및 GAN과 유사하게 모델 아키텍처의 설계는 고품질 샘플을 생성하는 데 중요한 역할을 한다.
이 작업에서 우리는 대부분 이미지 생성에 유용한 아키텍처에 초점을 맞추고, 다른 도메인에 대한 아키텍처 설계는 향후 작업으로 남겨둔다.
noise conditional score network s_θ(x, σ)의 출력은 입력 이미지 x와 동일한 모양을 가지고 있기 때문에 이미지의 밀도 예측(예: semantic segmentation)을 위해 성공적인 모델 아키텍처에서 영감을 얻는다.
실험에서, 우리의 모델 s_θ(x, σ)는 U-Net[46]의 아키텍처 설계를 dilated/atrous 컨볼루션[64, 65, 8]과 결합한다 - 이 두 가지 모두 semantic segmentation에서 매우 성공적인 것으로 입증되었다.
또한 일부 이미지 생성 작업[57, 13, 23]에서 우수한 성능에 영감을 받아 score 네트워크에서 instance normalization을 채택하고, 수정된 버전의 conditional instance normalization [13]을 사용하여 σ_i에 대한 conditioning을 제공한다.
아키텍처에 대한 자세한 내용은 부록 A에서 확인할 수 있습니다.
4.2 Learning NCSNs via score matching
sliced 및 denoising score matching은 NCSN을 학습시킬 수 있다.
노이즈로 섭동된 데이터 분포의 score를 추정하는 작업에 약간 빠르고 자연스럽게 적합하기 때문에 denoising score matching을 채택한다.
그러나 우리는 경험적으로 sliced score matching이 denoising score matching 뿐만 아니라 NCSN을 학습시킬 수 있다는 것을 강조한다.
우리는 노이즈 분포를 q_σ log(~x|x) = N(~x|x, σ^2 I)으로 선택한다; 따라서 ∇_~x log q_σ log(~x|x) = -(~x-x) / σ^2이다.
주어진 σ에 대해 denoising score matching 목표(식. (2))는

이다.
그런 다음, 우리는 모든 σ ∈ {σ_i}_(i=1)^L에 대해 식 (5)를 결합하여 하나의 통일된 objective

를 얻는다, 여기서 λ(σ_i) > 0은 σ_i에 따른 계수 함수이다.
s_θ(x, σ)가 충분한 용량을 가지고 있다고 가정하면, s_θ*(x, σ)는 모든 i ∈ {1, 2, ..., L}에 대해 s_θ*(x, σ_i) = ∇_x log q_(σ_i)(x) a.s인 경우에만 식 (6)를 최소화한다, 왜냐하면 식 (6)는 denoising score matching objective의 원추적인 조합이기 때문이다.
λ(·)는 다양하게 선택할 수 있습니다.
이상적으로, 우리는 모든 {σ_i}_(i=1)^L에 대한 λ(σ_i)l(θ; σ_i)의 값이 대략 같은 크기 순서이기를 바란다.
경험적으로, 우리는 score 네트워크가 최적화되도록 학습될 때 대략 |s_θ(x, σ)|_2 ∝ 1/σ를 가지고 있음을 관찰한다.
이것은 λ(σ) = σ^2를 선택하도록 영감을 준다.
왜냐하면 이 선택에 따라 λ(σ) l(θ; σ) = σ^2 l(θ; σ) = 1/2 E[|σ s_θ(~x,σ) + (~x - x) / σ|]가 되기 때문이다.
(~x - x) / σ ~N(0, I) 및 |σ s_θ(x, σ)| ∝ 1이므로 λ(σ) l(θ; σ)의 크기 순서는 σ에 의존하지 않는다고 쉽게 결론 내릴 수 있다.
우리는 우리의 objective 식 (6)이 적대적 학습, surrogate loss, 학습 중 score 네트워크의 샘플링을 필요로 하지 않는다는 것을 강조한다(예: 대조적 발산과 달리).
또한, 다루기 쉽도록 하기 위해 s_θ(x, σ)가 특별한 아키텍처를 가질 필요가 없다.
또한 λ(·)와 {σ_i}_(i=1)^L이 고정되면 서로 다른 NCSN을 정량적으로 비교하는 데 사용할 수 있다.

4.3 NCSN inference via annealed Langevin dynamics
NCSN s_θ(x, σ)가 학습된 후, 우리는 simulated annealing과 annealed importance sampling에서 영감을 받아 생성된 샘플에 대한 샘플링 접근법(annealed Langevin dynamics (알고리즘 1))을 제안한다.
알고리즘 1에 나온 것처럼, 우리는 고정된 prior 분포에서 샘플을 초기화함으로써 annealed Langevin dynamics를 시작한다, 예를 들어 균일한 노이즈.
그런 다음 단계 크기 α_1로 q_(σ_1)(x)에서 샘플을 추출하기 위해 Langevin dynamics를 실행한다.
다음으로, 우리는 이전 시뮬레이션의 최종 샘플에서 시작하여 축소된 단계 크기 α_2를 사용하여 q_(σ_2)(x)에서 샘플링하기 위해 Langevin dynamics를 실행한다.
우리는 이러한 방식으로 계속해서 q_(σ_(i-1))(x)에 대한 Langevin dynamics의 최종 샘플을 q_(σ_i)(x)에 대한 Langevin dynamics의 초기 샘플로 사용하고, α_i = ε · σ_i^2 / σ_L^2로 단계 크기 α_i를 점차 줄인다.
마지막으로, 우리는 σ_L = 0일 때 p_data(x)에 가까운 q_(σ_L)(x)에서 샘플링하기 위해 Langevin dynamics를 실행한다.
분포 {q_(σ_i)}_(i=1)^L은 모두 가우시안 노이즈에 의해 섭동되기 때문에, 그들의 지지는 전체 공간에 걸쳐 있고 score는 잘 정의되어 매니폴드 가설의 어려움을 피한다.
σ_1이 충분히 크면, q_(σ_1)(x)의 저밀도 영역은 작아지고 모드는 덜 고립된다.
앞에서 논의한 바와 같이, 이것은 score 추정을 더 정확하게 할 수 있고, Langevin dynamics의 혼합을 더 빠르게 할 수 있다.
따라서 우리는 Langevin dynamics가 q_(σ_1)(x)에 대한 좋은 샘플을 생성한다고 가정할 수 있다.
이 샘플들은 q_(σ_1)(x)의 고밀도 영역에서 나올 가능성이 높으며, 이는 q_(σ_1)(x)와 q_(σ_2)(x)가 서로 약간만 다르다는 점을 고려할 때 q_(σ_2)(x)의 고밀도 영역에도 존재할 가능성이 높다는 것을 의미한다.
score 추정과 Langevin dynamics가 고밀도 영역에서 더 잘 수행되므로, q_(σ_1)(x)의 샘플은 q_(σ_2)(x)의 Langevin dynamics에 대한 좋은 초기 샘플로 사용될 것이다.
마찬가지로, q_(σ_(i-1)) (x)는 q_(σ_i)(x)에 대한 좋은 초기 샘플을 제공하고, 마지막으로 q_(σ_L)(x)에서 좋은 품질의 샘플을 얻는다.

annealed Langevin dynamics의 효과를 입증하기 위해, 우리는 score만을 사용하여 잘 분리된 두 가지 모드를 가진 가우시안의 mixture에서 샘플링하는 것이 목표인 toy 예를 제공한다.
섹션 3.2에 사용된 가우시안 mixture의 샘플에 알고리즘 1을 적용합니다.
실험에서 우리는 L = 10, σ_1 = 10, σ_10 = 0.1인 기하급수로 {σ_i}_(i=1)^L을 선택한다.
결과는 그림 3에 제공된다.
그림 3(b)와 (c)를 비교하면, annealed Langevin dynamics는 두 모드 사이의 상대적 가중치를 정확하게 복구하는 반면, 표준 Langevin dynamics는 실패한다.
5 Experiments
이 섹션에서는 NCSN이 일반적으로 사용되는 여러 이미지 데이터 세트에서 고품질 이미지 샘플을 생성할 수 있음을 보여준다.
또한, 우리는 모델이 이미지 인페인팅 실험을 통해 합리적인 이미지 표현을 학습한다는 것을 보여준다.
Setup
우리는 실험에서 MNIST, CelebA[34] 및 CIFAR-10[31] 데이터세트를 사용한다.
CelebA의 경우 이미지가 먼저 중앙에서 140x140으로 잘라진 다음 32x32로 크기가 조정됩니다.
픽셀 값이 [0,1]이 되도록 모든 이미지의 스케일이 조정됩니다.
우리는 {σ_i}_(i=1)^L이 σ_1 = 1이고 σ_10 = 0.01인 기하학적 시퀀스가 되도록 L = 10개의 다른 표준 편차를 선택한다.
σ = 0.01의 가우시안 노이즈는 이미지 데이터에 대해 사람의 눈으로 거의 구별할 수 없습니다.
이미지 생성을 위해 annealed Langevin dynamics를 사용할 때, 우리는 T = 100과 ε = 2 x 10^-5를 선택하고 균일한 노이즈를 초기 샘플로 사용한다.
우리는 그 결과가 T의 선택과 관련하여 강력하다는 것을 발견했고, 5 x 10^-6과 5 x 10^-5 사이의 ε는 일반적으로 잘 작동한다.
부록 A와 B에서 모델 아키텍처 및 설정에 대한 추가 세부 정보를 제공합니다.


Image generation
그림 5에서, 우리는 MNIST, CelebA 및 CIFAR-10에 대한 annealed Langevin dynamics의 미처리 샘플을 보여준다.
샘플에서 알 수 있듯이, 생성된 이미지는 현대의 likelihood 기반 모델 및 GAN의 이미지와 더 높거나 유사한 품질을 가지고 있다.
annealed Langevin dynamics의 절차를 직관적으로 파악하기 위해, 우리는 그림 4에서 중간 샘플을 제공하는데, 여기서 각 행은 샘플이 순수 랜덤 노이즈에서 고품질 이미지로 어떻게 진화하는지 보여준다.
우리의 접근 방식의 더 많은 샘플은 부록 C에서 찾을 수 있다.
또한 부록 C.2의 학습 데이터세트에서 생성된 이미지의 가장 가까운 이웃을 보여줌으로써 모델이 단순히 학습 이미지를 기억하는 것이 아님을 입증한다.
많은 노이즈 레벨에 대해 conditional score 네트워크를 jointly 학습하고 annealed Langevin dynamics를 사용하는 것이 중요하다는 것을 보여주기 위해, 우리는 하나의 노이즈 레벨 {σ_1 = 0.01}만 고려하고 vanilla Langevin dynamics 샘플링 방법을 사용하는 베이스라인 접근법과 비교한다.
이 작은 추가 노이즈가 매니폴드 가설의 난이도를 우회하는 데 도움이 되지만(그림 1과 같이 노이즈가 추가되지 않으면 완전히 실패한다), 데이터 밀도가 낮은 영역의 score에 대한 정보를 제공하기에는 충분히 크지 않다.
결과적으로 이 베이스라인은 부록 C.1의 샘플에서 볼 수 있듯이 적절한 이미지를 생성하지 못합니다.

정량적 평가를 위해, 우리는 CIFAR-10에 대한 Inception [48] 및 FID[20] score를 표 1에 보고한다.
unconditional 모델로서, 우리는 클래스 conditional 생성 모델에 대해 보고된 대부분의 값보다 더 나은 8.87의 SOTA Inception score를 달성한다.
CIFAR-10에서 우리의 FID 점수 25.32는 SNGAN[36]과 같은 기존의 상위 모델과 비교할 수 있다.
이 두 데이터 세트의 score가 널리 보고되지 않고 서로 다른 전처리(예: CelebA의 중앙 크롭 크기)로 인해 직접 비교할 수 없는 숫자가 될 수 있기 때문에 MNIST와 CelebA의 score를 생략한다.

Image inpainting
그림 6에서, 우리는 score 네트워크가 다양한 이미지 인페인팅을 생성할 수 있도록 일반화되고 의미론적으로 의미 있는 이미지 표현을 학습한다는 것을 보여준다.
PixelCNN과 같은 일부 이전 모델은 래스터 스캔 순서로만 이미지를 귀속시킬 수 있습니다.
대조적으로, 우리의 방법은 annealed Langevin dynamics 절차의 간단한 수정(부록 B.3의 세부 사항)에 의해 임의의 모양이 막힌 이미지를 자연스럽게 처리할 수 있다.
부록 C.5에서 더 많은 이미지 인페인팅 결과를 제공합니다.
6 Related work
우리의 접근 방식은 샘플 생성을 위한 마르코프 체인의 transition 연산자를 학습하는 방법과 몇 가지 유사점이 있다[4, 51, 5, 16, 52].
예를 들어, 생성 확률적 네트워크(GSN [4, 1])는 평형 분포가 데이터 분포와 일치하는 마르코프 체인을 학습하기 위해 denoising autoencoder를 사용한다.
마찬가지로, 우리의 방법은 Langevin dynamics에서 사용되는 score 함수를 데이터 분포에서 샘플링하도록 학습시킨다.
그러나 GSN은 종종 학습 데이터 지점에 매우 가깝게 체인을 시작하므로 체인이 다른 모드 간에 빠르게 전환되어야 한다.
대조적으로, 우리의 annealed Langevin dynamics는 구조화되지 않은 노이즈에서 초기화된다.
Nonequilibrium Thermodynamics (NET [51])은 규정된 diffusion 과정을 사용하여 데이터를 랜덤 노이즈로 천천히 변환한 다음 inverse diffusion을 학습하여 이 과정을 역전시키는 방법을 배웠다.
그러나 NET은 diffusion 프로세스가 매우 작은 단계를 가져야 하고, 학습 시간에 수천 단계로 체인을 시뮬레이션해야 하기 때문에 확장성이 그리 높지 않다.
Infusion Training (IT[5]) 및 Variational Walkback (VW[16])과 같은 이전 접근 방식도 마르코프 체인 transition 연산자를 학습시키기 위해 서로 다른 노이즈 레벨/온도를 사용했다.
IT와 VW(NET 뿐만 아니라)는 모두 적절한 marginal likelihood의 증거 하한을 최대화하여 모델을 학습시킨다.
실제로는 variational autoencoder와 유사하게 블러 이미지 샘플을 생성하는 경향이 있다.
대조적으로, 우리의 목표는 likelihood 대신 score matching을 기반으로 하며, GAN과 유사한 이미지를 생성할 수 있다.
위에서 논의된 이전 방법과 우리의 접근 방식을 더욱 구별하는 몇 가지 구조적 차이가 있다.
첫째, 우리는 학습 중에 마르코프 체인에서 샘플을 추출할 필요가 없다.
대조적으로, GSN의 walkback 절차는 "negative samples"를 생성하기 위해 체인을 여러 번 실행해야 한다.
NET, IT 및 VW를 포함한 다른 방법도 학습 loss를 계산하기 위해 모든 입력에 대해 마르코프 체인을 시뮬레이션해야 한다.
이러한 차이는 심층 모델을 학습하기 위해 우리의 접근 방식을 더 효율적이고 확장 가능하게 만든다.
둘째, 우리의 학습과 샘플링 방법은 서로 분리된다.
score estimation에는 sliced 및 denoising score matching을 모두 사용할 수 있습니다.
샘플링에는 Langevin dynamics와 (잠재적으로) Hamiltonian Monte Carlo를 포함하여 score에 기초한 모든 방법이 적용된다[38].
우리의 프레임워크는 score 추정기와 (그래디언트 기반) 샘플링 접근 방식의 임의적인 조합을 허용하는 반면, 대부분의 이전 방법은 모델을 특정 마르코프 체인에 연결한다.
마지막으로, 우리의 접근 방식은 에너지 기반 모델의 그레디언트를 score 모델로 사용하여 에너지 기반 모델(EBM)을 학습하는 데 사용될 수 있다.
대조적으로, 마르코프 체인의 transition 연산자를 학습하는 이전의 방법이 EBM을 학습하는 데 어떻게 직접 사용될 수 있는지는 불분명하다.
score matching은 원래 EBM을 학습하기 위해 제안되었다.
그러나 score matching을 기반으로 하는 많은 기존 방법은 확장 가능하지 않거나 VAE 또는 GAN과 유사한 품질의 샘플을 생성하지 못한다[27, 49].
심층 에너지 기반 모델을 학습하는 데 있어 더 나은 성능을 얻기 위해, 일부 최근 연구는 대조적 발산에 의존하고 있으며, 학습과 테스트 모두에 대해 Langevin dynamics를 사용하여 샘플을 추출할 것을 제안한다[12, 39].
그러나 우리의 접근 방식과 달리 대조적 발산은 학습 중에 계산 비용이 많이 드는 Langevin dynamics의 절차를 내부 루프로 사용한다.
annealing과 denoising score matching을 결합하는 아이디어는 다른 맥락에서 이전 연구에서도 조사되었다.
[14, 7, 66]에서는 denoising autoencoder 학습을 위한 노이즈에 대한 다양한 annealing 스케줄이 제안된다.
그러나 그들의 작업은 생성 모델링 대신 분류의 성능을 향상시키기 위한 표현을 학습하는 것이다.
denoising score matching 방법은 또한 Stein의 Unbiased Risk Estimator [35, 56]의 기법을 사용하여 베이지안 최소 제곱의 관점에서 도출할 수 있다[43, 44].
7 Conclusion
우리는 먼저 score matching을 통해 데이터 밀도의 그래디언트를 추정한 다음 Langevin dynamics를 통해 샘플을 생성하는 score 기반 생성 모델링 프레임워크를 제안한다.
우리는 이 접근법의 나이브한 적용이 직면한 몇 가지 과제를 분석하고, Noise Conditional Score Networks(NCSN)을 학습하고 annealed Langevin dynamics로 샘플링하여 이를 해결할 것을 제안한다.
우리의 접근 방식은 적대적 학습, 학습 중 MCMC 샘플링, 특별한 모델 아키텍처가 필요하지 않다.
실험적으로, 우리는 우리의 접근 방식이 이전에는 최상의 likelihood 기반 모델과 GAN에 의해서만 생성되었던 고품질 이미지를 생성할 수 있음을 보여준다.
우리는 CIFAR-10에서 새로운 SOTA Inception score와 SNGAN에 필적하는 FID 점수를 달성한다.