2023. 3. 16. 12:00ㆍDiffusion
Deep Unsupervised Learning using Nonequilibrium Thermodynamics
Jascha Sohl-Dickstein, Eric A. Weiss, Niru Maheswaranathan, Surya Ganguli
Abstract
머신러닝의 중심 문제는 학습, 샘플링, 추론 및 평가가 여전히 분석적 또는 계산적으로 다루기 쉬운 매우 유연한 확률 분포 계열을 사용하여 복잡한 데이터 세트를 모델링하는 것이다.
여기서, 우리는 유연성과 추적성을 동시에 달성하는 접근법을 개발한다.
비평형 통계 물리학에서 영감을 받은 본질적인 아이디어는 반복적인 forward diffusion 과정을 통해 데이터 분포의 구조를 체계적으로 천천히 파괴하는 것이다.
그런 다음 데이터의 구조를 복원하여 데이터의 매우 유연하고 다루기 쉬운 생성 모델을 생성하는 reverse diffusion 프로세스를 학습한다.
이 접근 방식을 사용하면 수천 개의 레이어 또는 시간 단계를 사용하여 심층 생성 모델에서 확률을 신속하게 학습, 샘플링 및 평가할 수 있을 뿐만 아니라 학습된 모델에서 조건적 및 posterior 확률을 계산할 수 있다.
1. Introduction
역사적으로 확률론적 모델은 다음과 같은 두 가지 상충되는 objectives 사이에서 절충을 겪는다: 다루기 쉽고 유연함.
다루기 쉬운 모델은 분석적으로 평가할 수 있고 데이터(예: 가우시안 또는 라플라스)에 쉽게 적합할 수 있다.
그러나 이러한 모델은 풍부한 데이터 세트에서 구조를 적절하게 설명할 수 없다.
반면에 유연한 모델은 임의의 데이터에 구조를 맞도록 성형할 수 있습니다.
예를 들어, 유연한 분포 p(x) = φ(x)/Z를 산출하는 (음이 아닌) 함수 φ(x) 측면에서 모델을 정의할 수 있습니다, 여기서 Z는 정규화 상수입니다.
그러나 이 정규화 상수를 계산하는 것은 일반적으로 다루기 어렵다.
이러한 유연한 모델에서 샘플을 평가, 학습 또는 추출하려면 일반적으로 매우 비싼 Monte Carlo 프로세스가 필요하다.
예를 들어, 평균 필드 이론과 그 확장, 변형 베이즈, 대조적 발산, 최소 확률 흐름, 최소 KL 수축, 적절한 점수 규칙, 점수 매칭, 유사 가능성, 고리 모양의 믿음 전파 등을 개선하지만 제거하지는 않는 다양한 분석 근사치가 존재한다.
비모수 방법도 매우 효과적일 수 있습니다.
1.1. Diffusion probabilistic models
우리는 다음을 가능하게 하는 확률적 모델을 정의하는 새로운 방법을 제시한다:
1. 모델 구조의 극도의 유연성,
2. 정확한 샘플링,
3. 예를 들어 posterior를 계산하기 위해 다른 분포와의 쉬운 곱셈, 그리고
4. 모델 log-likelihood 및 개별 state의 확률을 저렴하게 평가할 수 있습니다.
우리의 방법은 마르코프 체인을 사용하여 한 분포를 점진적으로 다른 분포로 변환하는데, 이는 비평형 통계 물리학과 순차 Monte Carlo에서 사용되는 아이디어이다.
우리는 diffusion 과정을 사용하여 간단한 알려진 분포(예: 가우시안)를 타겟(데이터) 분포로 변환하는 생성 마르코프 체인을 구축한다.
이 마르코프 체인을 사용하여 달리 정의된 모델을 대략적으로 평가하는 대신, 우리는 확률론적 모델을 마르코프 체인의 끝점으로 명시적으로 정의한다.
diffusion 체인의 각 단계는 분석적으로 평가 가능한 확률을 가지기 때문에 전체 체인도 분석적으로 평가할 수 있다.
이 프레임워크에서의 학습은 diffusion 과정에 대한 작은 섭동를 추정하는 것을 포함한다.
작은 섭동을 추정하는 것은 분석적으로 정규화되지 않은 단일 잠재적 함수로 전체 분포를 명시적으로 설명하는 것보다 다루기 쉽다.
또한, 원활한 목표 분포를 위한 diffusion 과정이 존재하기 때문에, 이 방법은 임의의 형태의 데이터 분포를 캡처할 수 있다.
우리는 2차원 스위스 롤, 이진 시퀀스, 손으로 쓴 숫자(MNIST) 및 여러 자연 이미지(CIFAR-10, 나무껍질 및 낙엽) 데이터 세트에 대한 높은 log-likelihood 모델을 학습하여 이러한 diffusion 확률 모델의 유용성을 입증한다.
1.2. Relationship to other work
웨이크-슬립 알고리즘은 서로에 대한 추론과 생성 확률 모델을 학습하는 아이디어를 도입했다.
이 접근법은 일부 예외를 제외하고는 거의 20년 동안 거의 연구되지 않은 상태로 남아 있었다.
이 아이디어를 개발하는 작업이 최근 폭발적으로 증가하고 있다.
가변 학습 및 추론 알고리즘이 개발되어 잠재 변수에 대한 유연한 생성 모델과 posterior 분포가 서로에 대해 직접 학습될 수 있다.
이 논문들의 변형 경계는 우리의 학습 objective와 초기 연구에서 사용된 것과 유사하다.
그러나 우리의 동기와 모델 형태는 모두 상당히 다르며, 현재 작업은 이러한 기술과 관련하여 다음과 같은 차이점과 이점을 유지한다:
1. 우리는 다양한 베이지안 방법보다는 물리학, 준정적 프로세스 및 어닐링된 중요도 샘플링의 아이디어를 사용하여 프레임워크를 개발한다.
2. 우리는 학습된 분포를 다른 확률 분포(예: posterior를 계산하기 위해 조건적 분포)와 쉽게 곱하는 방법을 보여준다
3. 우리는 추론 모델과 생성 모델 사이의 objective의 비대칭으로 인해 추론 모델을 학습시키는 것이 변형 추론 방법에서 특히 어렵다는 것을 증명할 수 있는 어려움을 해결한다.
우리는 reverse(생성) process가 동일한 함수 형태를 갖도록 forward(추론) process를 단순한 함수 형태로 제한한다.
4. 우리는 몇 개의 레이어가 아니라 수천 개의 레이어(또는 시간 단계)로 모델을 학습시킨다.
5. 우리는 각 레이어(또는 시간 단계)의 엔트로피 생성에 대한 상한과 하한을 제공한다
생성 모델을 위해 매우 유연한 형태를 개발하거나 확률적 궤적을 학습하거나 베이지안 네트워크의 역전을 학습하는 확률론적 모델을 학습하기 위한 많은 관련 기술(아래 요약)이 있다.
가중치가 재조정된 웨이크-슬립은 원래 웨이크-슬립 알고리즘에 대한 확장과 개선된 학습 규칙을 개발한다.
생성 확률적 네트워크는 평형 분포를 데이터 분포와 일치하도록 마르코프 커널을 학습시킨다.
신경 자기 회귀 분포 추정기(및 반복 및 심층 확장)는 공동 분포를 각 차원에 걸쳐 다루기 쉬운 일련의 조건적 분포로 분해한다.
적대적 네트워크는 생성된 샘플을 실제 데이터와 구별하려는 분류기에 대해 생성 모델을 학습시킨다.
(Schmidhuber, 1992)의 유사한 objective는 약간 독립적인 단위를 가진 표현에 대한 양방향 매핑을 학습한다.
(Rippel & Adams, 2013; Dinh et al., 2014)에서는 단순 요인 밀도 함수를 사용하여 잠재 표현에 대한 이항 결정론적 맵을 학습한다.
(Stuhlmürler et al., 2013)에서 베이지안 네트워크에 대한 확률적 역을 학습한다
조건적 가우시안 스케일 혼합물(MCGSM)의 혼합물은 일련의 인과적 이웃에 따라 달라지는 매개 변수와 함께 가우시안 스케일 혼합물을 사용하는 데이터 세트를 설명한다.
신경망이 생성 모델로 도입된 (MacKay, 1995)과 잠재 공간에서 데이터 공간으로 확률적 다양체 매핑을 학습하는 (Bishop et al., 1998)을 포함하여 간단한 잠재 분포에서 데이터 분포로의 유연한 생성 매핑을 학습하는 중요한 작업이 추가로 있다.
우리는 적대적 네트워크 및 MCGSM과 실험적으로 비교할 것이다.
물리학의 관련 아이디어로는 머신러닝에서 Annealed Importance Sampling (AIS)으로 알려진 Jarzynski 등식이 있는데, 이는 정규화 상수의 비율을 계산하기 위해 한 분포를 천천히 다른 분포로 변환하는 마르코프 체인을 사용한다.
(Burda et al., 2014)에서는 AIS가 전방 궤적이 아닌 역방향 궤적을 사용하여 수행될 수 있음을 보여준다.
Fokker-Planck 방정식의 확률적 실현인 Langevin dynamics는 타겟 분포를 평형으로 하는 가우시안 diffusion 과정을 정의하는 방법을 보여준다.
(Suykens & Vandewallle, 1995)에서 Fokker-Planck 방정식은 확률적 최적화를 수행하는 데 사용된다.
마지막으로, Kolmogorov의 순방향 및 역방향 방정식은 많은 forward diffusion 과정에서 reverse diffusion 과정이 동일한 함수 형태를 사용하여 설명될 수 있음을 보여준다.

2. Algorithm
우리의 목표는 모든 복잡한 데이터 분포를 단순하고 다루기 쉬운 분포로 변환하는 forward(또는 추론) diffusion 프로세스를 정의한 다음 생성 모델 분포를 정의하는 이 diffusion 프로세스의 유한 시간 reversal을 학습하는 것이다(그림 1 참조).
우리는 먼저 forward 추론 diffusion 프로세스를 설명한다.
그런 다음 reverse 생성 diffusion 프로세스를 학습하고 확률을 평가하는 데 사용할 수 있는 방법을 보여준다.
또한 reverse 프로세스에 대한 엔트로피 한계를 도출하고 학습된 분포에 두 번째 분포를 곱하는 방법을 보여준다(예: 이미지를 인페인팅하거나 디노이징할 때 posterior를 계산하는 방법).
2.1. Forward Trajectory
우리는 데이터 분포 q(x^(0))에 레이블을 붙인다.
데이터 분포는 π(y)에 대한 마르코프 diffusion 커널 T_π(y|y';β)의 반복 적용에 의해 점진적으로 잘 작동하는(분석적으로 다루기 쉬운) 분포 π(y)로 변환됩니다, 여기서 β는 diffusion 속도입니다,
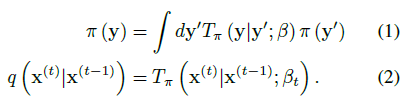
따라서 데이터 분포에서 시작하여 diffusion의 T단계를 수행하는 것에 해당하는 forward 궤적은

이다.
아래에 표시된 실험의 경우, q(x^(t)|x^(t-1))는 동일성-공분산을 가진 가우시안 분포로의 가우시안 diffusion 또는 독립적인 이항 분포로의 이항 diffusion에 해당한다.
표 App.1은 가우시안 분포와 이항 분포 모두에 대한 diffusion 커널을 제공한다.

2.2. Reverse Trajectory
생성 분포는 동일한 궤적을 설명하도록 학습되지만, reverse로

가우시안과 이항 diffusion 모두에서 연속 diffusion(작은 단계 크기의 한계)의 경우 diffusion 프로세스의 reversal은 forward 프로세스와 동일한 함수 형태를 갖는다(Feller, 1949).
q(x^(t)|x^(t-1))는 가우시안(이항 분포)이므로 t가 작으면 q(x^(t-1)|x^(t))도 가우시안(이항 분포)이 된다.
궤도가 길수록 diffusion 속도 β는 더 작아질 수 있다.
학습하는 동안 가우시안 diffusion 커널에 대한 평균과 공분산 또는 이항 커널에 대한 비트 플립 확률만 추정하면 된다.
표 App.1에 나타난 바와 같이, f_μ(x^(t), t)와 f_∑(x^(t, t)는 가우시안에 대한 reverse 마르코프 transition의 평균과 공분산을 정의하는 함수이며, f_b(x^(t), t)는 이항 분포에 대한 비트 플립 확률을 제공하는 함수이다.
이 알고리즘을 실행하는 데 드는 계산 비용은 이 함수들의 비용으로, 시간 단계의 수를 곱한 것이다.
이 논문의 모든 결과에 대해, 다층 퍼셉트론은 이러한 함수를 정의하는 데 사용된다.
그러나 비모수적 방법을 포함하여 광범위한 회귀 또는 함수 적합 기술이 적용될 수 있다.
2.3. Model Probability
생성 모형이 데이터에 할당할 확률은
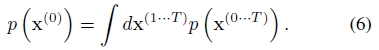
입니다.
나이브하게도 이 적분은 다루기 어렵지만, 어닐링된 중요성 샘플링과 Jarzynski 등식에서 힌트를 얻어, 우리는 대신 forward 궤적에 걸쳐 평균화된 forward 및 reverse 궤적의 상대 확률을 평가한다.
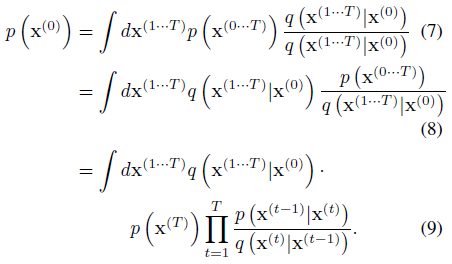
이것은 forward 궤적 q(x^(1...T)|x^(0))의 샘플을 평균하여 신속하게 평가할 수 있다.
무한소 β의 경우 궤적에 대한 forward 및 reverse 분포를 동일하게 만들 수 있습니다(섹션 2.2 참조).
만약 그것들이 동일하다면, 위의 적분을 정확하게 평가하기 위해서는 q(x^(1...T)|x^(0))의 단일 샘플만 필요하다.
이것은 통계 물리학에서 준정적 과정의 경우에 해당한다.
2.4. Training
학습은 Jenson의 부등식에 의해 제공되는 하한을 갖는 모델 log likelihood
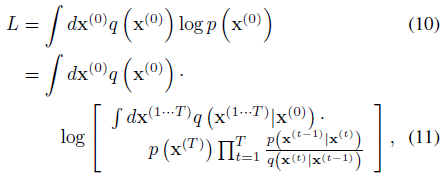
을 최대화하는 것과 같다
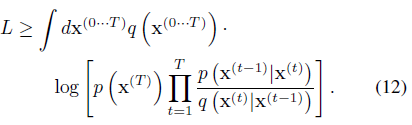
부록 B에서 설명한 바와 같이, 우리의 diffusion 궤적에 대해 이것은 엔트로피와 KL 발산을 분석적으로 계산할 수 있는

로 감소한다.
이 경계의 파생은 다양한 베이지안 방법에서 경계된 log likelihood의 파생과 유사하다.
섹션 2.3에서와 같이, 준정적 과정에 해당하는 forward 궤적과 reverse 궤적이 동일한 경우, 식 13의 부등식이 동일하게 됩니다.
학습은 log likelihood에서 이 하한을 최대화하는 reverse 마르코프 transition을 찾는 것으로 구성된다,

가우시안 및 이항 diffusion에 대한 구체적인 추정 타겟은 표 App.1에 제시되어 있다.
따라서 확률 분포를 추정하는 작업은 가우시안 시퀀스의 평균과 공분산을 설정하는(또는 베르누이 테스트 시퀀스의 상태 플립 확률을 설정하는) 함수에 대한 회귀를 수행하는 작업으로 축소되었다.
2.4.1 Setting the Diffusion Rate β_t
forward 궤적에서 t를 선택하는 것은 학습된 모델의 성능에 중요하다.
AIS에서 중간 분포의 올바른 스케줄은 로그 파티션 함수 추정의 정확도를 크게 향상시킬 수 있다.
열역학에서 평형 분포 사이를 이동할 때 취하는 스케줄은 얼마나 많은 자유 에너지가 손실되는지를 결정한다.
가우시안 diffusion의 경우, 우리는 K의 그래디언트 상승에 의해 forward diffusion 스케줄 β_(2...T)를 학습한다.
첫 번째 단계의 분산 β_1은 과적합을 방지하기 위해 작은 상수로 고정됩니다.
q(x^(1...T)|x^(0) b_(1...T)로부터의 샘플 의존성 (Kingma & Welling, 2013)에서와 같이 '동결 노이즈'를 사용하여 명시한다.
이 노이즈는 추가적인 보조 변수로 취급되며 매개변수에 대해 K의 부분 미분을 계산하는 동안 일정하게 유지된다.
이항 diffusion의 경우, 이산 상태 공간은 동결된 노이즈가 있는 그래디언트 상승을 불가능하게 한다.
대신 forward diffusion 스케줄 β_(1...T) diffusion 단계당 원래 신호의 일정한 부분 1/T를 지워서 β_t = (T - t + 1)^-1의 diffusion 속도를 산출한다.
2.5. Multiplying Distributions, and Computing Posteriors
신호 디노이징 또는 누락된 값의 추론을 수행하기 위해 posterior를 계산하는 것과 같은 작업은 두 번째 분포를 가진 모델 분포 p(x^(0))의 곱셈 또는 경계가 있는 양의 함수 r(x^(0))을 필요로 하며, 새로운 분포 ~p(x^(0)) ∝ p(x^(0))r(x^(0))을 생성한다.
분포를 곱하는 것은 변형 오토 인코더, GSN, NADE 및 대부분의 그래픽 모델을 포함한 많은 기술에 비용이 많이 들고 어렵다.
그러나 diffusion 모델에서는 두 번째 분포가 diffusion 과정의 각 단계에 대한 작은 섭동으로 취급되거나 종종 각 diffusion 단계로 정확하게 곱될 수 있기 때문에 간단합니다.
그림 3 및 5는 자연 이미지의 디노이징 및 인페인팅을 수행하기 위한 diffusion 모델의 사용을 보여줍니다.
다음 섹션에서는 diffusion 확률 모델의 맥락에서 분포를 곱하는 방법을 설명합니다.


2.5.1 Modified Marginal Distributions
먼저 ~p(x^(0))를 계산하기 위해 각 중간 분포에 해당 함수 r(x^(t))을 곱한다.
우리는 분포 또는 마르코프 transition 위의 타일드를 사용하여 그것이 이런 식으로 수정된 궤적에 속한다는 것을 나타낸다.
~p(x^(0...T)) 수정된 reverse 궤적이며, 분포 ~p(x^(T)) = 1/~Z_T p(x^(T)) r(x^(T))에서 시작하여 중간 분포의 시퀀스

를 진행한다, 여기서 ~Z_t는 t번째 중간 분포에 대한 정규화 상수이다.
2.5.2 Modified Diffusion Steps
reverse diffusion 프로세스에 대한 마르코프 커널 p(x^(t)|x^(t+1))는 평형 조건

을 따른다.
우리는 섭동된 마르코프 커널 ~p(x^(t)|x^(t+1))이 대신 섭동된 분포에 대한 평형 조건을 따르기를 바란다,

식 20은

일 때 만족할 것이다.
식 21은 정규화된 확률 분포에 해당하지 않을 수 있으므로, 우리는 ~p(x^(t)|x^(t+1))를 상응하는 정규화된 분포

로 선택한다, 여기서 ~Z_t(x^(t+1))는 정규화 상수이다.
가우시안의 경우, 각 diffusion 단계는 작은 분산 때문에 일반적으로 r(x^(t))에 비해 매우 급격하게 정점을 이룬다.
이는 r(x^(t)) / r(x^(t+1))이 p(x^(t)|x^(t+1))에 대한 작은 섭동으로 취급될 수 있음을 의미한다.
가우시안에 대한 작은 섭동은 평균에 영향을 미치지만 정규화 상수에는 영향을 미치지 않으므로, 이 경우 식 21과 22는 동등하다(부록 C 참조).
2.5.3 Applying r(x^(t))
r(x^(t))이 충분히 smooth하다면, reverse diffusion 커널 p(x^(t)|x^(t+1))에 대한 작은 섭동으로 처리될 수 있다.
이 경우 ~p(x^(t)|x^(t+1))는 p(x^(t)|x^(t+1))와 동일한 함수 형태를 갖지만 가우시안 커널에 대한 섭동 평균 또는 이항 커널에 대한 섭동된 플립 속도를 가질 것이다.
섭동된 diffusion 커널은 표 App.1에 나와 있으며, 부록 C의 가우시안에 대해 도출되었다.
r(x^(t))을 닫힌 형태의 가우시안(또는 이항) 분포로 곱할 수 있다면, 닫힌 형태의 reverse diffusion 커널 p(x^(t)|x^(t+1))로 직접 곱할 수 있다.
이것은 그림 5의 인페인팅 예제에서와 같이 r(x^(t))이 좌표의 일부 부분 집합에 대한 델타 함수로 구성된 경우에 적용된다.
2.5.4 Choosing r(x^(t))
일반적으로, r(x^(t))은 궤적의 프로세스에서 천천히 변화하도록 선택되어야 한다.
이 논문의 실험을 위해 우리는 상수로 선택했다,

또 다른 편리한 선택은 r(x^(t)) = r(x^(0))^((T-t)/T)이다.
이 두 번째 선택에서 r(x^(t))은 reverse 궤적에 대한 시작 분포에 기여하지 않는다.
이는 reverse 궤적에 대해 ~p(x^(T))에서 초기 샘플을 그리는 것이 간단함을 보장한다.
2.6. Entropy of Reverse Process
forward 프로세스가 알려져 있기 때문에, 우리는 reverse 궤적에서 각 단계의 조건부 엔트로피에 대한 상한과 하한을 도출할 수 있으며, 따라서 상한과 하한 모두 q(x^(1...T)|x^(0))에만 의존하고 분석적으로 계산할 수 있다.
파생상품은 부록 A에 수록되어 있다.
3. Experiments
우리는 다양한 연속 데이터 세트와 이진 데이터 세트에 대한 diffusion 확률 모델을 학습한다.
그런 다음 학습된 모델의 샘플링과 누락된 데이터의 인페인팅을 시연하고 모델 성능을 다른 기술과 비교한다.
모든 경우에 objective 함수와 그래디언트는 Theano를 사용하여 계산되었다.
모델 학습은 CIFAR-10을 제외하고 SFO와 함께 했다.
CIFAR-10 결과는 알고리즘의 오픈 소스 구현과 최적화를 위한 RMSprop을 사용했다.
우리 모델이 제공하는 log likelihood의 하한은 표 1의 모든 데이터 세트에 대해 보고된다.

3.1. Toy Problems
3.1.1 Swiss Roll
diffusion 확률론적 모델은 radial 기저 함수 네트워크를 사용하여 f_μ(x^(t), t)와 f_∑(x^(t), t)를 생성하는 2차원 스위스 롤 분포로 구축되었다.
그림 1에 나타난 바와 같이, 스위스 롤 분포는 성공적으로 학습되었다.
자세한 내용은 부록 섹션 D.1.1을 참조하십시오.
3.1.2 Binary Heartbeat Distribution
diffusion 확률 모델은 길이 20의 간단한 이진 시퀀스에 대해 학습되었는데, 여기서 1은 5번째 시간 bin마다 발생하고 나머지 bin은 0이다.
다층 퍼셉트론을 사용하여 reverse 궤적의 베르누이 속도 f_b(x^(t), t)를 생성한다.
실제 분포에서의 log likelihood는 시퀀스당 log2(1/5) = -2.322비트입니다.
그림 2와 표 1에서 볼 수 있듯이 학습은 거의 완벽했습니다.
자세한 내용은 부록 섹션 D.1.2를 참조하십시오.

3.2. Images
우리는 여러 이미지 데이터 세트에서 가우시안 diffusion 확률 모델을 학습시켰다.
이러한 실험에서 공유하는 다중 스케일 컨볼루션 아키텍처는 부록 섹션 D.2.1에 설명되어 있으며 그림 D.1에 설명되어 있다.


3.2.1 Datasets
MNIST
간단한 데이터 세트에 대한 이전 작업과 직접 비교할 수 있도록 MNIST 숫자에 대해 학습했다.
(Bengio et al., 2012; Bengio & Thibodeau-Laufer, 2013; Goodfello et al., 2014)에 관련된 log likelihood는 표 2에 제시되어 있다.
MNIST 모델의 샘플은 부록 그림 App.1에 제시되어 있다.
우리의 학습 알고리즘은 log likelihood에 대해 점근적으로 일관된 하한을 제공한다.
그러나 연속 MNIST log likelihood에 대한 이전에 보고된 대부분의 결과는 모델 샘플에서 계산된 Parzen-window 기반 추정치에 의존한다.
따라서 이 비교를 위해 우리는 (Goodfello et al., 2014)과 함께 릴리스된 Parzen-window 코드를 사용하여 MNIST 로log likelihood를 추정한다.
CIFAR-10
확률론적 모델은 CIFAR-10 챌린지 데이터 세트에 대한 학습 이미지에 적합했다.
학습된 모델의 샘플은 그림 3에 나와 있습니다.
Dead Leaf Images
Dead Leaf Images는 스케일에 대한 멱함수 분포에서 그린 겹겹의 폐색 원으로 구성된다.
그것들은 분석적으로 다루기 쉬운 구조를 가지고 있지만, 자연 이미지의 많은 통계적 복잡성을 포착하기 때문에 자연 이미지 모델에 대한 설득력 있는 테스트 사례를 제공한다.
표 2와 그림 4에 설명된 바와 같이, 우리는 Dead Leaves 데이터 세트에서 SOTA 성능을 달성한다.

Bark Texture Images
(Lazebnik et al., 2005)의 Bark Texture Images(T01-T04)에 대해 확률론적 모델이 학습되었다.
이 데이터 세트의 경우 그림 5의 모델 posterior의 샘플을 사용하여 누락된 데이터의 광범위한 영역을 그려서 posterior 분포를 평가하거나 생성하는 것이 간단하다는 것을 보여준다.
4. Conclusion
우리는 확률의 정확한 샘플링과 평가를 가능하게 하는 확률 분포를 모델링하기 위한 새로운 알고리즘을 도입했고 도전적인 자연 이미지 데이터 세트를 포함하여 다양한 토이 및 실제 데이터 세트에 대한 효과를 입증했다.
이러한 각 테스트에 대해 우리는 유사한 기본 알고리즘을 사용하여 우리의 방법이 다양한 분포를 정확하게 모델링할 수 있음을 보여주었다.
대부분의 기존 밀도 추정 기술은 다루기 쉽고 효율적으로 유지하기 위해 모델링 능력을 희생해야 하며 샘플링 또는 평가는 종종 매우 비싸다.
우리 알고리즘의 핵심은 데이터를 노이즈 분포에 매핑하는 마르코프 diffusion 체인의 reversal을 추정하는 것으로 구성된다; 단계 수가 커짐에 따라 각 diffusion 단계의 reversal 분포는 간단하고 추정하기 쉬워진다.
결과는 모든 데이터 분포에 대한 적합성을 학습할 수 있지만 학습, 정확한 샘플 추출 및 평가가 용이하고 조건적 및 posterior 분포를 조작하는 것이 쉬운 알고리즘이다.