4D Gaussian Splatting for Real-Time Dynamic Scene Rendering

4D Gaussian Splatting for Real-Time Dynamic Scene Rendering

 

Guanjun Wu, Taoran Yi, Jiemin Fang, Lingxi Xie, Xiaopeng Zhang, Wei Wei, Wenyu Liu, Qi Tian, Xinggang Wang

 

Abstract

동적 장면을 표현하고 렌더링하는 것은 중요하지만 어려운 작업이었습니다.

특히 복잡한 모션을 정확하게 모델링하기 위해서는 일반적으로 높은 효율성을 보장하기가 어렵습니다.

실시간 동적 장면 렌더링을 달성하는 동시에 높은 학습 및 저장 효율성을 누리기 위해 저희는 각 프레임에 3D-GS를 적용하는 대신 동적 장면에 대한 전체적인 표현으로 4D Gaussian Splatting (4D-GS)을 제안합니다.

4D-GS에서는 3D Gaussians과 4D 신경 복셀을 모두 포함하는 새로운 명시적 표현이 제안됩니다.

4D 신경 복셀에서 Gaussian 피쳐를 효율적으로 구축한 다음 경량 MLP를 적용하여 새로운 타임스탬프에서 Gaussian 변형을 예측합니다.

저희의 4D-GS 방법은 이전의 SOTA 방법과 비슷하거나 더 나은 품질을 유지하면서 RTX 3090 GPU에서 800×800 해상도에서 고해상도 82FPS의 실시간 렌더링을 달성합니다.

 

그림 1. 우리의 방법은 높은 렌더링 품질을 유지하면서 높은 이미지 해상도에서 동적 장면에 대한 실시간 렌더링을 달성합니다. 오른쪽 그림은 도트의 반경이 학습 시간에 해당하는 합성 데이터 세트에서 테스트됩니다. "Res": 해상도.

1. Introduction

Novel view synthesis (NVS)은 3D 비전 영역에서 중요한 작업으로 자리 잡고 있으며 VR, AR 및 영화 제작과 같은 많은 응용 프로그램에서 중요한 역할을 합니다.

NVS는 원하는 시점이나 장면의 타임스탬프에서 이미지를 렌더링하는 것을 목표로 하며, 일반적으로 여러 2D 이미지에서 장면을 정확하게 모델링해야 합니다.

동적 장면은 실제 시나리오에서 매우 흔하며, 공간적 및 시간적으로 희소한 입력으로 복잡한 모션을 모델링해야 하기 때문에 렌더링이 중요하지만 어렵습니다.

 

NeRF [22]는 암시적 함수로 장면을 표현함으로써 새로운 뷰 이미지를 합성하는 데 큰 성공을 거두었습니다.

볼륨 렌더링 기술 [5]은 2D 이미지와 3D 장면을 연결하기 위해 도입되었습니다.

그러나 원래의 NeRF 방법은 큰 학습 및 렌더링 비용을 부담합니다.

일부 NeRF 변형 [4, 6–8, 23, 34, 36]이 학습 시간을 며칠에서 몇 분으로 단축하지만 렌더링 프로세스는 여전히 무시할 수 없는 지연 시간을 갖습니다.

 

최근의 3D Gaussian Splatting (3D-GS)[14]은 장면을 3D Gaussians로 표현하여 렌더링 속도를 실시간 수준으로 크게 향상시킵니다.

원래 NeRF의 번거로운 볼륨 렌더링은 효율적인 미분 가능한 스플래팅 [46]으로 대체되어 3D Gaussian 포인트를 2D 평면에 직접 투영합니다.

3D-GS는 실시간 렌더링 속도를 즐길 뿐만 아니라 장면을 더 명확하게 표현하여 장면 표현을 조작하기가 더 쉽습니다.

 

그러나 3D-GS는 정적 장면에 초점을 맞추고 있습니다.

4D 표현으로 동적 장면으로 확장하는 것은 합리적이고 중요하지만 어려운 주제입니다.

핵심 과제는 희소 입력에서 복잡한 포인트 모션을 모델링하는 데 있습니다.

3D-GS는 포인트와 같은 Gaussians이 있는 장면을 표현함으로써 자연스러운 지오메트리 prior를 유지합니다.

한 가지 직접적이고 효과적인 확장 접근 방식은 각 타임스탬프 [21]에서 3D Gaussians을 구성하는 것이지만, 특히 긴 입력 시퀀스의 경우 저장/메모리 비용이 배가될 것입니다.

저희의 목표는 학습과 렌더링 효율성, 즉 4D Gaussian Splatting (4D-GS)을 모두 유지하면서 컴팩트한 표현을 구성하는 것입니다.

이를 위해 시간 공간 구조 인코더와 매우 작은 멀티-헤드 Gaussian deformation 디코더를 포함하는 효율적인 Gaussian deformation 필드 네트워크에 의해 Gaussian 움직임과 모양 변화를 표현할 것을 제안합니다.

canonical 3D Gaussian 세트는 하나만 유지됩니다.

각 타임스탬프에 대해 canonical 3D Gaussian은 Gaussian deformation 필드에 의해 새로운 모양을 가진 새로운 위치로 변환됩니다.

변환 프로세스는 Gaussian 모션과 deformation을 모두 나타냅니다.

각 Gaussian의 모션을 개별적으로 모델링하는 것과 달리 [21, 44], 공간-시간 구조 인코더는 인접한 서로 다른 3D Gaussians을 연결하여 보다 정확한 모션과 모양 변형을 예측할 수 있습니다.

그런 다음 변형된 3D Gaussians을 시간 스탬프 이미지를 렌더링하기 위해 직접 분할할 수 있습니다.

저희의 기여는 다음과 같이 요약할 수 있습니다.

 • 시간에 따른 Gaussian 모션과 Gaussian 모양 변화를 모두 모델링하여 효율적인 Gaussian deformation 필드를 가진 효율적인 4D Gaussian splatting 프레임워크를 제안합니다.
 • 효율적인 공간-시간 구조 인코더에 의해 인근 3D Gaussaisn을 연결하고 풍부한 3D Gaussian 피쳐를 구축하기 위한 멀티-해상도 인코딩 방법이 제안됩니다.
 • 4D-GS는 합성 데이터 세트의 경우 800×800 해상도에서 최대 82FPS, 실제 데이터 세트의 경우 1352×1014 해상도에서 30FPS의 동적 장면에서 실시간 렌더링을 달성하는 동시에 이전의 SOTA 방법과 비교하거나 우수한 성능을 유지하고 4D 장면에서 편집 및 추적 가능성을 보여줍니다.

 

 

2. Related Works

이 섹션에서는 섹션 2.1의 동적 NeRF의 차이점을 간단히 검토한 다음 섹션 2.2의 포인트 클라우드 기반 신경 렌더링 알고리즘에 대해 설명합니다.

 

2.1. Dynamic Neural Rendering

[3, 22, 48]은 암시적 래디언스 필드가 장면 표현을 효과적으로 학습하고 고품질의 새로운 뷰를 합성할 수 있음을 보여줍니다.

[24, 25, 28]은 정적 가설에 도전하여 동적 장면에 대한 새로운 뷰 합성의 경계를 확장했습니다.

또한 [6]은 명시적 복셀 그리드를 사용하여 시간 정보를 모델링할 것을 제안하여 동적 장면의 학습 시간을 30분으로 가속화하고 [12, 20, 45]에 적용합니다.

제안된 canonical 매핑 신경 렌더링 방법은 그림 2(a)에 나와 있습니다.

[4, 8, 17, 34, 37]은 분해된 신경 복셀을 채택하여 더 빠른 동적 장면 학습의 추가 발전을 나타냅니다.

이들은 그림 2(b)와 같이 각 타임스탬프에서 샘플링된 포인트를 개별적으로 처리합니다.

[11, 18, 27, 38, 40, 42]는 멀티뷰 설정을 처리하는 효율적인 방법입니다.

앞서 언급한 방법은 빠른 학습 속도를 달성하지만 특히 단안 입력의 경우 동적 장면에 대한 실시간 렌더링은 여전히 어렵습니다.

저희의 방법은 희소 입력의 경우에도 품질을 유지하면서 그림 2(c)에서 매우 효율적인 학습 및 렌더링 파이프라인을 구성하는 것을 목표로 합니다.

그림 2. 서로 다른 동적 장면 렌더링 방법의 예시. (a) 포인트는 볼륨 렌더링 중에 캐스트된 ray에서 샘플링됩니다. [6, 28]에서 제안된 포인트 변형 필드는 포인트를 canonical 공간으로 매핑합니다. (b) 시간 인식 볼륨 렌더링은 각 포인트의 피쳐를 직접 계산하고 렌더링 경로를 변경하지 않습니다. (c) Gaussian deformation 필드는 원래의 3D Gaussians을 특정 타임스탬프를 가진 다른 3D Gaussians 그룹으로 변환합니다.

2.2. Neural Rendering with Point Clouds

3D 장면을 효과적으로 표현하는 것은 여전히 어려운 주제입니다.
커뮤니티는 다양한 신경 표현 [22], 예를 들어 메시, 포인트 클라우드 [43] 및 하이브리드 접근 방식을 탐구했습니다.

포인트 클라우드 기반 방법 [19, 29, 30, 47]은 초기에 3D 세그멘테이션 및 분류를 타겟으로 합니다.

[1, 43]에 제시된 렌더링을 위한 대표적인 접근 방식은 포인트 클라우드 표현과 볼륨 렌더링을 결합하여 빠른 수렴 속도를 달성합니다.

[15, 16, 31]은 장면 재구성을 위해 미분가능한 포인트 렌더링 기술을 채택합니다.

또한 3D-GS [14]는 순수한 명시적 표현 및 미분 가능한 포인트 기반 splatting 방법으로 유명하여 새로운 뷰의 실시간 렌더링을 가능하게 합니다.

Dynamic3DGS [21]는 각 타임스탬프 t_i에서 각 3D Gaussians의 위치와 분산을 추적하여 동적 장면을 모델링합니다.

명시적 테이블을 사용하여 모든 타임스탬프에 각 3D Gaussians에 대한 정보를 저장하면 O(tN)로 표시되는 선형 메모리 소비가 증가합니다.

장기적인 장면 재구성의 경우 저장 비용을 무시할 수 없게 됩니다.

저희 접근 방식의 메모리 복잡성은 3D Gaussians의 수와 Gaussians deformation 필드 네트워크 F의 매개변수에만 의존하며, 이는 O(N + F)로 표시됩니다.

[44]는 원래 3D Gaussians에 한계 시간 Gaussian 분포를 추가하여 3D Gaussians을 4D로 상향 조정합니다.

그러나 각 3D Gaussian이 로컬 시간 공간에만 초점을 맞추게 할 수 있습니다.

저희의 접근 방식은 또한 3D Gaussian 모션을 모델링하지만 컴팩트한 네트워크를 사용하여 매우 효율적인 학습 효율성과 실시간 렌더링을 얻을 수 있습니다.

 

 

3. Preliminary

이 섹션에서는 섹션 3.1의 3D-GS [14]의 표현 및 렌더링 프로세스와 섹션 3.2의 동적 NeRF 공식을 간단히 검토합니다.

 

3.1. 3D Gaussian Splatting

3D Gaussaisn [14]는 포인트 클라우드 형태의 명시적인 3D 장면 표현입니다.

각각의 3D Gaussian은 공분산 행렬 Σ 및 중심점 X로 특징지어지며, 이를 가우시안의 평균값이라고 합니다:

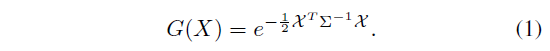
미분 가능한 최적화를 위해 공분산 행렬  Σ를 스케일링 행렬 S와 회전 행렬 R로 분해할 수 있습니다:

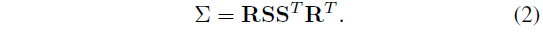
새로운 뷰를 렌더링할 때 카메라 평면 내의 3D Gaussians에는 differential splatting [46]이 사용됩니다.

[50]에서 소개한 바와 같이, 투영 변환의 아핀 근사치의 뷰 변환 행렬 W와 자코비안 행렬 J를 사용하여 카메라 좌표의 공분산 행렬 Σ'을

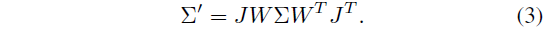
으로 계산할 수 있습니다.

요약하면, 각 3D Gaussian은 다음과 같은 속성으로 특징지어집니다: 위치 X ∈ R^3, spherical harmonic (SH) 계수 C ∈ R^k(여기서 k는 SH 함수들의 수들을 나타낸다), 불투명도 α ∈ R, 회전 인자 r ∈R^4 및 스케일링 인자 s ∈ R^3에 의해 정의되는 컬러.

구체적으로, 각 픽셀에 대해, 모든 Gaussian들의 컬러 및 불투명도는 Gaussian 표현 식 1을 사용하여 계산됩니다.

픽셀에 중첩되는 N개의 정렬된 점들의 블렌딩은 다음 공식에 의해 제공됩니다:

여기서 c_i, α_i는 공분산 Σ이 있는 3D Gaussian G에 의해 계산된 이 점의 밀도와 색상에 최적화 가능한 점당 불투명도 및 SH 색상 계수를 곱한 것을 나타냅니다.

 

3.2. Dynanic NeRFs with Deformation Fields

모든 동적 NeRF 알고리즘은

로 공식화할 수 있으며, 여기서 M은 6D 공간(x, d, t)을 4D 공간(c, σ)에 매핑하는 매핑입니다. 

동적 NeRF는 주로 두 가지 경로를 따릅니다: canonical-매핑 볼륨 렌더링 [6, 20, 24, 25, 28] 및 시간 인식 볼륨 렌더링 [4, 8, 9, 17, 34].

이 섹션에서는 주로 전자에 대한 간략한 검토를 제공합니다.

 

그림 2(a)와 같이, canonical-매핑 볼륨 렌더링은 deformation 네트워크 ϕ_t: (x, t) → Δx에 의해 샘플링된 각 포인트를 canonical 공간으로 변환합니다.
그런 다음 canonical 네트워크 ϕ_x가 도입되어 각 ray에서 볼륨 밀도와 뷰 의존적 RGB 색상을 회귀합니다.

렌더링 공식은

으로 표현할 수 있으며, 여기서 'NeRF'는 vanilla NeRF 파이프라인을 나타냅니다.

 

그러나 우리의 4D Gaussian splatting 프레임워크는 새로운 렌더링 기술을 제시합니다.

저희는 시간 t에서 Gaussian deformation 필드 네트워크 F를 사용하여 3D Gaussians을 직접 변환하고 differentail splatting [14]을 따릅니다.

 

 

4. Method

섹션 4.1에서는 전체 4D Gaussian Splatting 프레임워크를 소개합니다.

그런 다음 섹션 4.2에서 Gaussian deformation 필드를 제안합니다.

마지막으로 섹션 4.3에서 최적화 프로세스를 설명합니다.

그림 3. 모델의 전체 파이프라인. 3D Gaussians G 그룹이 주어지면, 멀티-해상도 복셀 평면을 쿼리하여 복셀 피쳐를 계산하기 위해 각 3D Gaussians X 및 타임스탬프 t의 중심 좌표를 추출합니다. 그런 다음 작은 멀티-헤드 Gaussian deformation 디코더를 사용하여 피쳐를 디코딩하고 타임스탬프 t에서 deformed 3D Gaussians G'를 얻습니다. 그런 다음 deformed Gaussians은 렌더링된 이미지로 splatt됩니다.

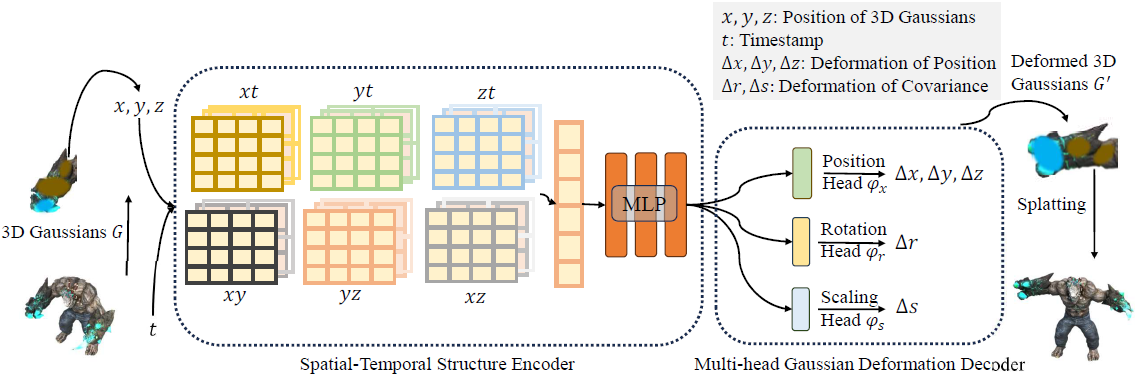
4.1. 4D Gaussian Splatting Framework

그림 3과 같이 뷰 행렬 M = [R, T], 타임스탬프 t가 주어지면 4D Gaussian splatting 프레임워크는 3D Gaussian G 및 Gaussian deformation 필드 네트워크 F를 포함합니다.

그런 다음 새로운 뷰 이미지 ^I는 ^I = S(M, G') 다음에 S를 differential splatting [46]하여 렌더링되며, 여기서 G' = ΔG + G입니다.

 

구체적으로, 3D Gaussian ΔG의 deformation은 Gaussian deformation 필드 네트워크 ΔG = F(G, t)에 의해 도입되며, 여기서 공간-시간적 구조 인코더 H는 3D Gaussians f_d = H(G, t)의 시간적 및 공간적 피쳐를 모두 인코딩할 수 있으며, 멀티-헤드 Gaussian deformation 디코더 D는 피쳐를 디코딩하고 각 3D Gaussian의 deformation ΔG = D(f)를 예측할 수 있으며, 이 후 deformed 3D Gaussians G'를 도입할 수 있습니다.

 

4D Gaussian Splatting의 렌더링 프로세스는 그림 2(c)에 나와 있습니다.

4D Gaussian splatting은 원래의 3D Gaussians G를 타임스탬프 t가 주어진 다른 3D Gaussians G' 그룹으로 변환하여 [46]에서 언급된 differential splatting의 효과를 유지합니다.

 

4.2. Gaussian Deformation Field Network

Gaussian deformation 필드를 학습하기 위한 네트워크에는 효율적인 공간-시간 구조 인코더 H와 각 3D Gaussian의 deformation을 예측하기 위한 Gaussian deformation 디코더 D가 포함됩니다.

 

Spatial-Temporal Structure Encoder.

근처의 3D Gaussians은 항상 유사한 공간 및 시간 정보를 공유합니다.

3D Gaussians의 피쳐를 효과적으로 모델링하기 위해 멀티-해상도 HexPlane R(i, j)와 [4, 6, 8, 34]에서 영감을 받은 작은 MLP ϕ_d를 포함한 효율적인 공간-시간 구조 인코더 H를 소개합니다.

vanilla 4D 신경 복셀은 메모리 소모가 크지만 4D K-Plane [8] 모듈을 채택하여 4D 신경 복셀을 6개의 평면으로 분해합니다.

특정 영역의 모든 3D Gaussians은 경계면 복셀에 포함될 수 있으며 Gaussian의 deformation은 근처의 시간 복셀에도 인코딩될 수 있습니다.

 

구체적으로, 공간-시간 구조 인코더 H는 6개의 멀티-해상도 평면 모듈 R_l(i, j)과 작은 MLP ϕ_d, 즉 H(G, t) = {R_l(i, j), ϕ_d|(i, j) ∈ {(x, y), (x, z), (y, z), (x, t), (y, t), (z, t), l ∈ {1, 2}를 포함합니다.

위치 X = (x, y, z)는 3D Gaussians G의 평균값입니다.

각 복셀 모듈은 R(i, j) ∈ R^(h x lN_i x lN_j)로 정의되며, 여기서 h는 피쳐의 숨겨진 차원을 나타내고, N은 복셀 그리드의 기본 해상도를 나타내며, l은 업샘플링 스케일과 같습니다.

이는 시간 정보를 고려하면서 6개의 2D 복셀 평면 내에서 3D Gaussians의 인코딩 정보를 수반합니다.

별도의 복셀 피쳐를 계산하는 공식은 다음과 같습니다:

f_h ∈ R^(h ∗ l)는 신경복셀의 피쳐입니다.

'interp'는 격자의 4개 꼭지점에 위치한 복셀 피쳐를 조회하기 위한 쌍선형 보간법을 의미합니다.

생산 과정에 대한 설명은 [8]과 비슷합니다.

그러면 작은 MLP ϕ_d가 모든 피쳐를 f_d = ϕ_d(f_h)만큼 병합합니다.

 

Multi-head Gaussian Deformation Decoder.

3D Gaussians의 모든 피쳐가 인코딩되면 멀티헤드 Gaussian deformation 디코더 D = {ϕ_x, ϕ_r, ϕ_s}로 원하는 변수를 계산할 수 있습니다.

위치 ΔX = ϕ_x(f_d), 회전 Δr = ϕ_r(f_d), 스케일링 Δs = ϕ_s(f_d)의 deformation을 계산하기 위해 별도의 MLP가 사용됩니다.

그런 다음 deformed 피쳐 (X', r', s')을

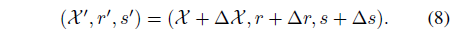
로 처리할 수 있습니다.

마지막으로 deformed 3D Gaussians G' = {X', s', r', σ, C}를 얻습니다.

 

4.3. Optimization

3D Gaussian Initialization.

[14]는 3D Gaussians이 structure from motion (SfM) [32] 포인트 초기화로 잘 학습될 수 있음을 보여줍니다.

마찬가지로, 4D Gaussians도 적절한 3D Gaussians 초기화에서 파인튜닝되어야 합니다.

저희는 웜업을 위해 초기 3000번의 반복에서 3D Gaussians을 최적화한 다음 4D Gaussians ˆI = S(M, G') 대신 3D Gaussians ˆI = S(M, G')로 이미지를 렌더링합니다.

최적화 프로세스의 그림은 그림 4에 나와 있습니다.

그림 4. 최적화 과정의 예시. 정적 3D Gaussians 초기화를 통해 저희 모델은 모션 파트의 고품질 3D Gassians을 학습할 수 있습니다.

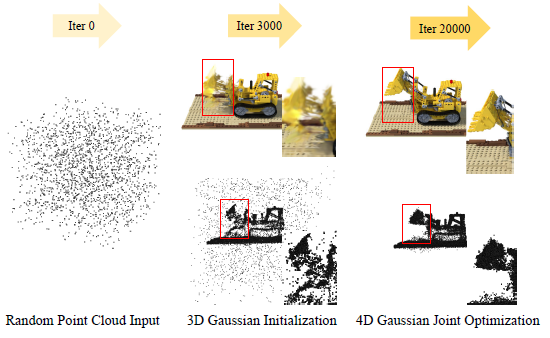
Loss Function.

다른 재구성 방법 [6, 14, 28]과 마찬가지로 L1 색상 loss를 사용하여 학습 과정을 supervise합니다.

그리드 기반 total-variational loss [4, 6, 8, 36] L_tv도 적용됩니다.

 

5. Experiments

이 섹션에서는 주로 섹션 5.1 설정의 하이퍼파라미터와 데이터 세트를 소개하고 서로 다른 데이터 세트 간의 결과를 섹션 5.2의 [2, 4, 6, 8, 14, 18, 35, 37, 38]과 비교합니다.

그런 다음 섹션 5.3에서 접근 방식의 효과를 입증하기 위한 ablation 연구를 제안하고 섹션 5.4에서 4D-GS에 대한 더 많은 논의를 제안합니다.

마지막으로 섹션 5.5에서 제안한 4D-GS의 한계에 대해 논의합니다.

 

5.1. Experimental Settings

우리의 구현은 주로 PyTorch [26] 프레임워크를 기반으로 하며 단일 RTX 3090 GPU에서 테스트되었으며, 3D-GS [14]에 설명된 구성으로 최적화 매개변수를 파인튜닝했습니다.

더 많은 하이퍼파라미터는 부록에 나와 있습니다.

 

Synthetic Dataset.

저희는 주로 D-NeRF [28]에서 소개한 synthetic 데이터 세트를 사용하여 모델의 성능을 평가합니다.

이러한 데이터 세트는 단안 설정을 위해 설계되었지만, 각 타임스탬프에 대한 카메라 포즈는 랜덤으로 생성되는 것에 가깝습니다.

이러한 데이터 세트 내의 각 장면에는 50~200개의 동적 프레임이 포함되어 있습니다.

그림 5. 합성된 데이터셋을 다른 모델과 비교한 시각화 [4, 6, 8, 12, 14, 37]. [8]의 렌더링 결과는 기본 녹색 배경으로 표시됩니다. 렌더링 설정을 채택했습니다.

Real-world Datasets.

저희는 real-world 시나리오에서 모델의 성능을 평가하기 위해 HyperNeRF [25]와 Neu3D의 [17]에서 제공하는 데이터 세트를 벤치마크 데이터 세트로 활용합니다.

Nerfies 데이터 세트는 간단한 카메라 동작에 이어 하나 또는 두 개의 카메라를 사용하여 캡처되고 Neu3D의 데이터 세트는 15~20개의 정적 카메라를 사용하여 캡처됩니다.

저희는 Neu3D의 데이터 세트에서 각 비디오의 첫 번째 프레임에서 SfM [32]으로 계산된 포인트와 HyperNeRF에서 랜덤으로 선택된 200개의 프레임을 사용합니다.

그림 6. 다른 방법과 비교한 HyperNeRF[25] 데이터 세트의 시각화 [6, 12, 14, 25]. 'GT'는 ground truth 이미지를 의미합니다.

5.2. Results

우리는 주로 peak-signal-to-noise ratio (PSNR), 지각 품질 측정 LPIPS[49], structural similarity index (SSIM)[41] 및 구structural dissimilarity index measure (DSSIM), multiscale structural similarity index (MS-SSIM), FPS, 학습 시간 및 저장을 포함한 확장을 포함한 다양한 메트릭을 사용하여 실험 결과를 평가합니다.

표 1. synthetic 데이터 세트에 대한 정량적 결과. 최상의 결과와 차상위 결과는 분홍색과 노란색으로 표시됩니다. 렌더링 해상도는 800×800으로 설정됩니다. 표의 "time"은 학습 시간을 나타냅니다.

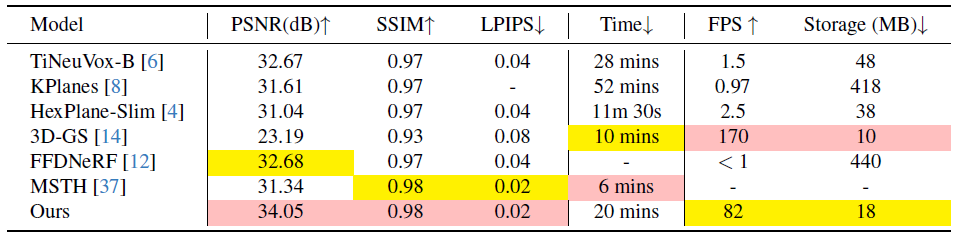
새로운 뷰 합성의 품질을 평가하기 위해 저희는 해당 분야의 [4, 6, 8, 14, 37]을 포함한 여러 SOTA 방법에 대한 벤치마킹을 수행했습니다.

결과는 표 1에 요약되어 있습니다.

현재의 동적 하이브리드 표현은 고품질 결과를 생성할 수 있지만 렌더링 속도가 빠르다는 단점이 있는 경우가 많습니다.

동적 모션 부분을 모델링하지 않기 때문에 [14]는 동적 장면을 재구성하지 못합니다.

이에 반해 저희 방법은 매우 낮은 스토리지 소비와 수렴 시간을 유지하면서 synthetic 데이터 세트 내에서 최고의 렌더링 품질과 매우 빠른 렌더링 속도를 모두 누릴 수 있습니다.

표 2. HyperNeRF의 [25] vrig 데이터 세트에 대한 정량적 결과 렌더링 해상도는 960×540로 설정됩니다.

표 3. Neu3D의 [17] 데이터 세트에 대한 정량적 결과, 렌더링 해상도는 1352×1014로 설정됩니다.

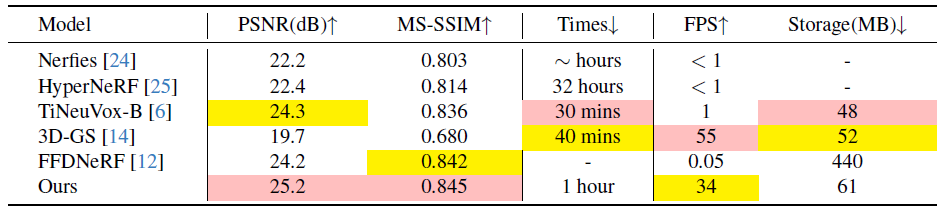
또한 real-world 데이터 세트에서 얻은 결과는 표 2와 표 3에 나와 있습니다.

일부 NeRF [2, 4, 35]는 수렴 속도가 느리고, 다른 그리드 기반 NeRF 방법 [4, 6, 8, 37]은 복잡한 객체 세부 정보를 캡처하려고 시도할 때 어려움을 겪는 것이 분명합니다.

이와는 대조적으로, 우리의 방법은 유사한 렌더링 품질, 빠른 수렴을 연구하며 실내의 경우 프리-뷰 렌더링 속도가 우수합니다.

[18]은 저희와 비교하여 고품질을 다루지만, 다중 캠 설정의 필요성으로 인해 단안 장면을 모델링하기가 어렵고 다른 방법으로도 프리-뷰 렌더링 속도와 저장이 제한됩니다.

 

5.3. Ablation Study

Spatial-Temporal Structure Encoder.

명시적인 HexPlane 인코더 R_l(i, j)은 3D Gaussians의 공간 및 시간 정보를 유지할 수 있는 용량을 가지고 있어 순수하게 명시적인 방법에 비해 스토리지 소비를 줄일 수 있습니다 [21].

이 모듈을 폐기하면 얕은 MLP ϕ_d만 사용하면 다양한 설정에서 복잡한 deformation을 모델링하는 데 부족하다는 것을 알 수 있습니다.

표 4는 모델이 최소한의 메모리 비용을 발생시키지만 렌더링 품질을 희생시키는 것을 보여줍니다.

표 4. 우리가 제안한 방법을 사용한 synthetic 데이터 세트에 대한 ablation 연구.

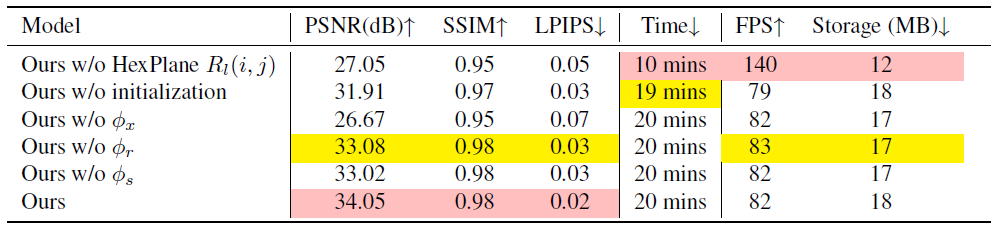
Gaussian Deformation Decoder.

저희가 제안한 Gaussian deformation 디코더 D는 공간-시간 구조 인코더 H에서 피쳐를 디코딩합니다.

3D Gaussians의 모든 변화는 별도의 MLP {ϕ_x, ϕ_r, ϕ_s}를 통해 설명할 수 있습니다.

표 4에서 볼 수 있듯이 4D Gaussians은 3D Gaussians 모션을 모델링하지 않으면 동적 장면에 잘 맞지 않습니다.

한편, 인체 관절의 모션은 일반적으로 거시적인 관점에서 표면 세부 사항의 스트레칭과 비틀림으로 나타납니다.

이러한 모션을 정확하게 모델링하는 것을 목표로 하는 경우 3D Gaussians의 크기와 모양도 그에 따라 조정해야 합니다.

그렇지 않으면 과도한 스트레칭 중 세부 사항이 과소 적합되거나 미시적 수준에서 물체의 모션을 올바르게 시뮬레이션할 수 없습니다.

그림 7은 또한 3D Gaussians의 모양 deformation이 세부 사항을 복구하는 데 중요하다는 것을 보여줍니다.

그림 7. 회전 및 스케일링 디코더의 ablation 연구. 'ds'는 ϕ_s를 나타내고, 'dr'은 ϕ_r을 나타냅니다.

3D Gaussian Initialization.

SfM [32] 포인트 초기화가 없는 경우에 따라 4D-GS를 직접 학습하면 수렴에 어려움이 발생할 수 있습니다.

웜업을 위한 3D Gaussians 최적화:

 (a) 일부 3D Gaussians을 동적 부분에 머물게 하고, 이는 그림 4와 같이 4D Gaussians에 의한 큰 deformation 학습의 압력을 해제합니다.

 (b) 적절한 3D Gaussians G를 학습하고 그림 8(c)와 같이 동적 부분에 더 많은 주의를 기울여 deformation 필드를 제안합니다.

 (c) Gaussian deformation 네트워크 F를 최적화하고 학습 프로세스를 안정적으로 유지하는 데 있어 숫자 오류를 방지합니다.

표 4는 또한 웜업 coarse 단계 없이 모델을 학습하면 렌더링 품질이 저하된다는 것을 보여줍니다.

그림 8. HexPlane 복셀 그리드의 시각화. (a)는 렌더링된 이미지입니다. (b)는 공간 복셀 그리드의 매개변수이며, 이는 3D Gaussians의 피쳐가 명시적인 그리드로 인코딩되었음을 의미합니다. (c)는 그리드의 시간적 피쳐이며, 각 열은 타임스탬프의 공간적 피쳐를 나타냅니다.

5.4. Discussions
Analysis of Multi-resolution HexPlane Gaussian Encoder.

멀티-해상도 HexPlane R_l(i, j)의 피쳐 시각화는 그림 8에 나와 있습니다.

명시적 모듈로서 모든 3D Gaussians 피쳐는 개별 복셀 평면에서 쉽게 최적화될 수 있습니다.

복셀 평면이 가장자리와 같은 렌더링된 이미지와 유사한 모양을 보이는 것도 그림 8 (b)에서 관찰할 수 있습니다.

한편, 시간적 피쳐는 그림 8 (c)의 움직임 영역에도 남아 있습니다.

이러한 명시적 표현은 4D Gaussians의 학습 속도와 렌더링 품질을 향상시킵니다.

 

Tracking with 3D Gaussians.

3D로 추적하는 것도 중요한 작업입니다.

[12]는 물체의 움직임을 3D로 추적하는 방법도 보여줍니다.

dynamic3DGS [21]과 달리, 저희의 방법은 저장 공간이 상당히 낮은 단안 설정, 즉 3D Gaussians G에서 10MB, Gaussian deformation 필드 네트워크 F에서 8MB의 추적 물체를 제시할 수도 있습니다.

그림 9는 특정 타임스탬프에서 3D Gaussian의 deformation을 보여줍니다.

그림 9. 3D Gaussians을 사용한 추적의 시각화. 두 번째 행 그림의 각 선은 3D Gaussians의 궤적을 나타냅니다.

 

그림 10. 4D Gaussians으로 구도의 시각화.

Composition with 4D Gaussians.

dynamic3DGS [21]와 유사하게, 우리가 제안한 방법은 그림 10에서 다른 4D Gaussians을 사용한 구성도 제안할 수 있습니다.

3D Gaussians을 명시적으로 표현한 덕분에 모든 학습된 모델은 G' = {G'_1, G'_2, ..., G'_n}에 이어 동일한 공간에서 deformed 3D Gaussians을 예측할 수 있으며, differential rendering [46]은 모든 포인트 클라우드를 ˆI = S(M, G')의 시점으로 투영할 수 있습니다.

그림 11. 렌더링된 화면에서 렌더링 속도와 3D Gaussians의 수 사이의 관계를 시각화합니다. 모든 테스트는 synthesis 데이터 세트에서 끝납니다.

Analysis of Rendering Speed.

그림 11과 같이 800×800 해상도에서 렌더링된 화면의 포인트와 렌더링 속도 간의 관계도 테스트합니다.

렌더링된 포인트가 30000보다 낮으면 렌더링 속도가 최대 90까지 가능하다는 것을 발견했습니다.

Gaussian deformation 필드의 구성은 부록에서 설명합니다.

렌더링 시간 렌더링 속도를 달성하려면 모든 렌더링 해상도, 3D Gaussians 수를 포함한 4D Gaussians 표현, Gaussian deformation 필드 네트워크의 용량 및 기타 하드웨어 제약 조건 간의 균형을 맞춰야 합니다.

 

5.5. Limitations

4D-GS는 많은 시나리오에서 빠른 수렴을 달성하고 실시간 렌더링 결과를 얻을 수 있지만 해결해야 할 몇 가지 주요 과제가 있습니다.

첫째, 큰 움직임, 배경점의 부재 및 부정확한 카메라 포즈로 인해 4D Gaussians을 최적화하는 데 어려움이 있습니다.

또한 4D-GS는 추가 supervision 없이 단안 설정에서 정적 및 동적 Gaussiansparts의 관절 움직임을 분할할 수 없습니다.

마지막으로, 막대한 수의 3D Gaussians에 의한 Gaussian deformation 필드의 쿼리가 많기 때문에 도시 규모의 재구성을 처리하기 위해 보다 소형화된 알고리즘을 설계해야 합니다.

 

 

6. Conclusion

이 논문에서는 실시간 동적 장면 렌더링을 달성하기 위해 4D Gaussian splatting을 제안합니다.

효율적인 deformation 필드 네트워크는 Gaussain 모션과 모양 deformations을 정확하게 모델링하기 위해 구성되며, 여기서 인접한 Gaussians은 시공간 구조 인코더를 통해 연결됩니다.

Gaussian 간의 연결은 더 완벽한 변형 지오메트리로 이어져 반발을 효과적으로 피할 수 있습니다.

우리의 4D Gaussians은 동적 장면을 모델링할 수 있을 뿐만 아니라 4D 객관적인 추적 및 편집 가능성도 있습니다.